-
mars 2026 : Sur les ponts de Paris

-
mars 2026 : Conjecture de Goldbach, parcours eulérien et point fixe en dimension 1

-
24 février 2026 : Conjecture de Goldbach et points fixes d'un projecteur (en bleu, pourquoi j’ai un problème)

-
22 février 2026 : Conjecture de Goldbach et symétrie

-
février 2026 : Euler à nouveau, un lemme au sujet de carrés et de rectangles
 Variae Demonstrationes Geometriae Variae Demonstrationes Geometriae  
-
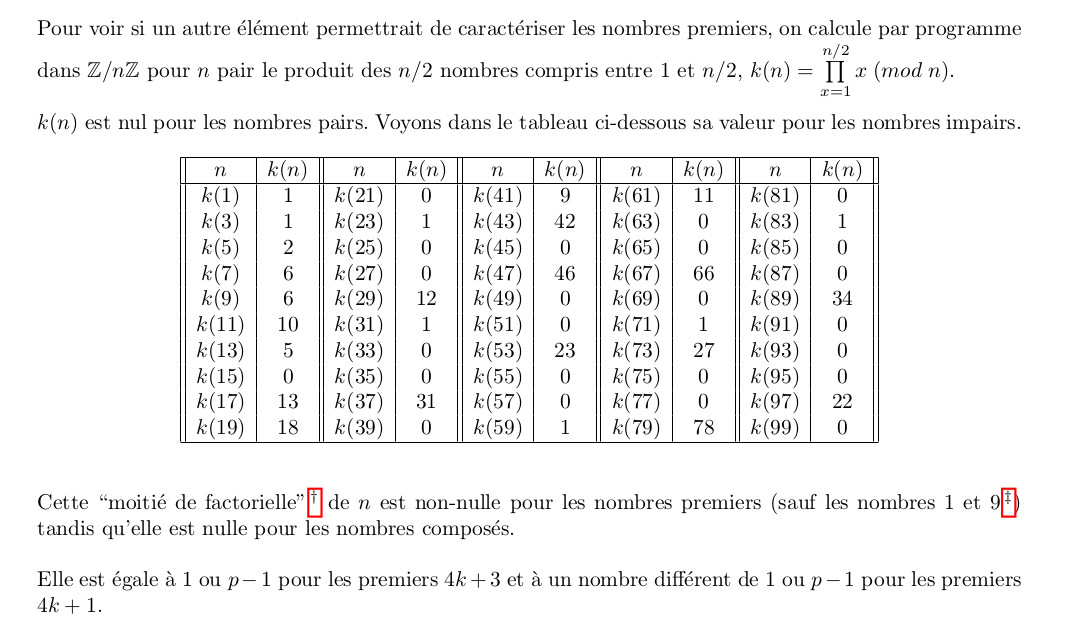
février 2026 : petit calcul d'Euler qui montre le léger déséquilibre entre les premiers 4k+1 et les premiers 4k-1, voir
 , à la page 5. , à la page 5. 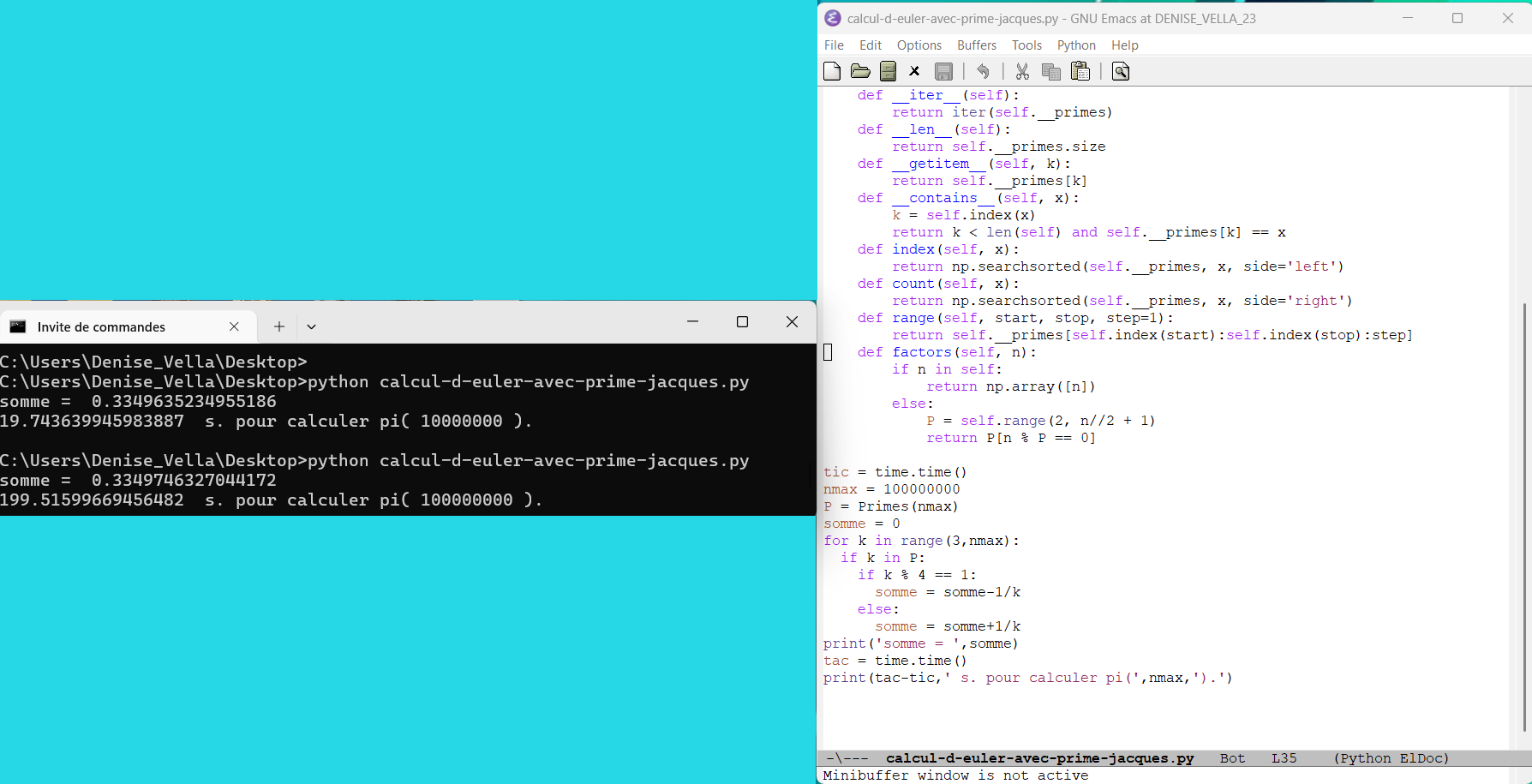
-
♠ octobre 2025 : reprise de l’approche géométrique dans le plan complexe
 (en) (en)  sur Hal sur Hal  version html version html 

-
♥ janvier 2026 : rappel formule simple utilisant la fonction de Lambert (voir programme de décembre 2024)
 
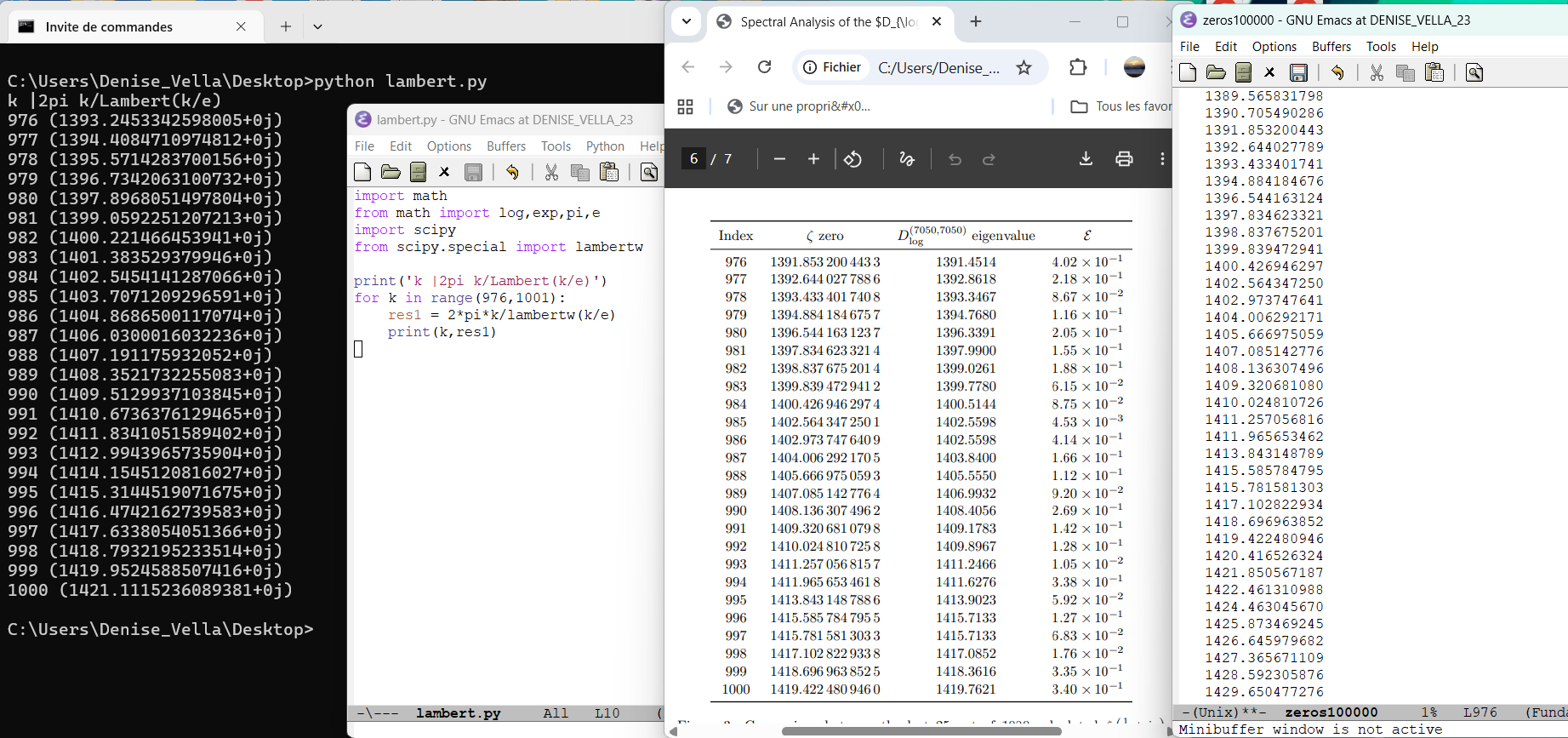
-
♥ décembre 2024 : zéros de zeta, fonction W de Lambert
 Tentative de simplification Tentative de simplification  Référence au sujet de la fonction de Lambert Référence au sujet de la fonction de Lambert  
-
♥♥ 9.11.2024 : démonstration d’une découverte qu’on avait faite en février 2024, au sujet de la somme des inverses des racines carrées des nombres entiers positifs (voir étonnement constant 22.2.2024)

Après tout, l’idée initiale d’Euler... 
-
♥♥ 22.2.2024 : exponentielle et logarithme : Des intérêts composés (petit encart devoir d’Évariste, et dédicace spéciale à grand-papa Lulu, qui m’a appris à factoriser, et le célèbre holorime aussi) (745)
 étonnement constant étonnement constant  Compléments par Pierre de la Harpe Compléments par Pierre de la Harpe  de ce fait, image du résultat d’un programme python d’expression du log par une racine "beaucoup"-ième de ce fait, image du résultat d’un programme python d’expression du log par une racine "beaucoup"-ième    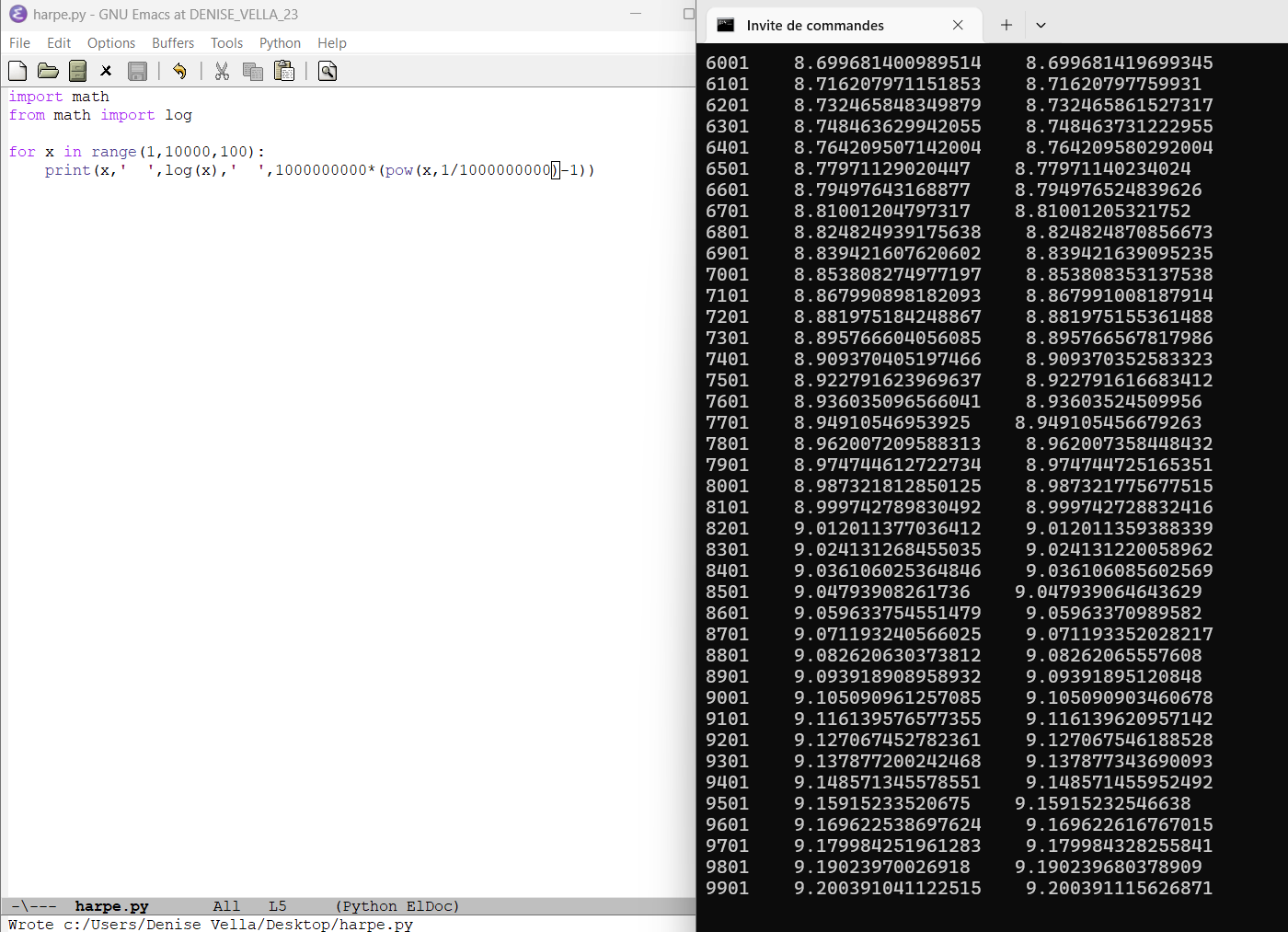
-
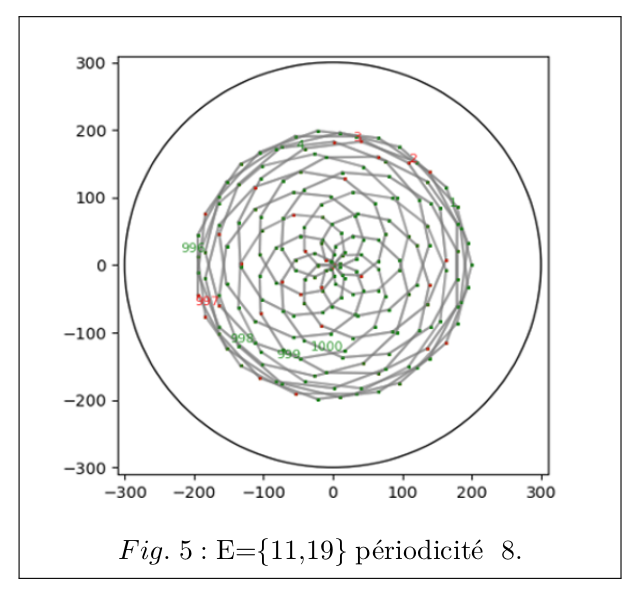
♥♥ 10.7.2019 : un ensemble, une transformation, des traces de premiers (575)
 
-
♥♥ 5.3.2019 : comment perçoit-on ? (titre : Spectre lumineux) où apparaît mystérieusement une fonction triangulaire (541)

-
♥♥ 29.11.2017 : à chaque primorielle, le nombre de points fixes augmente d’une puissance de 2. (438)

-
♥♥ Fractales (45)

-
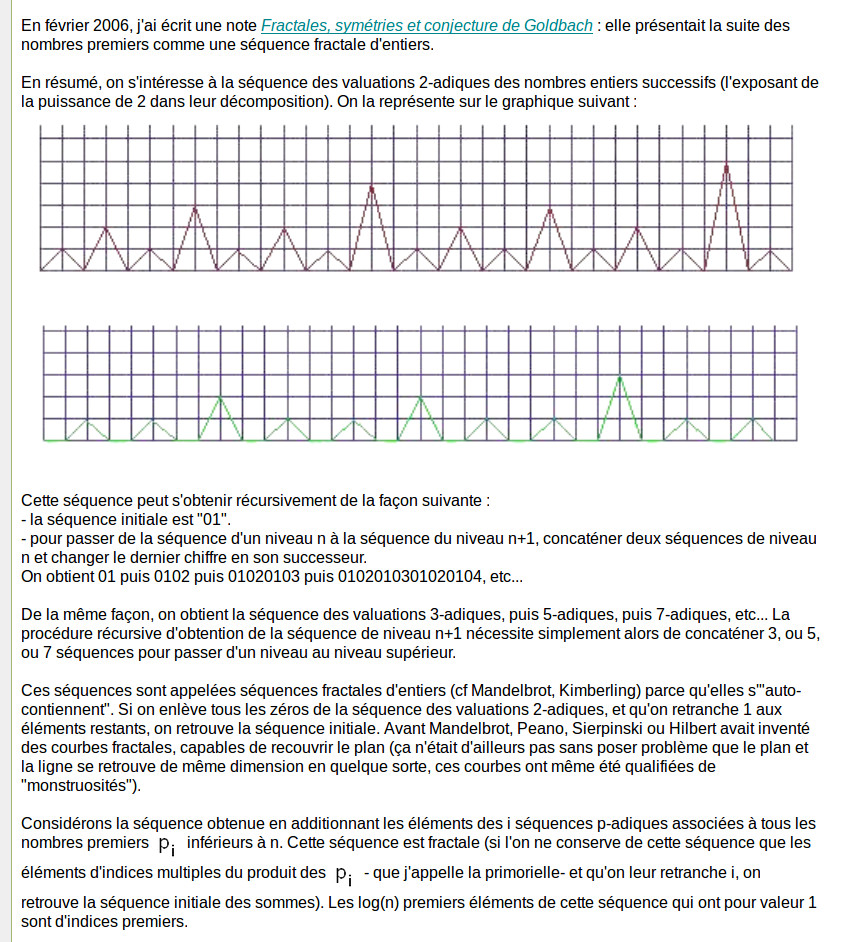
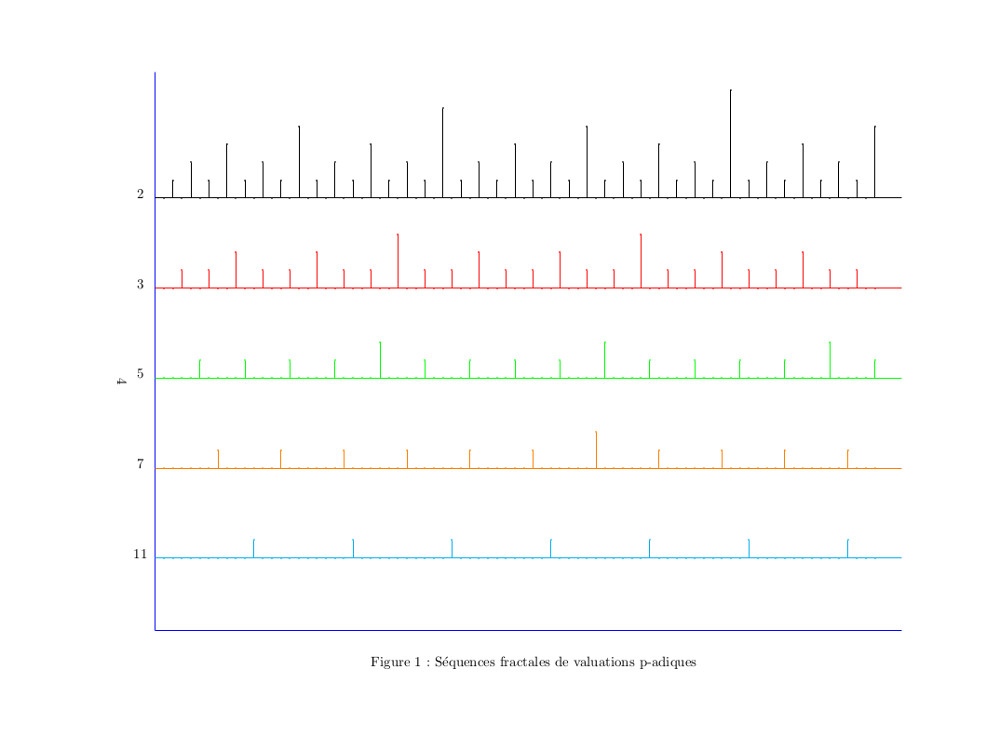
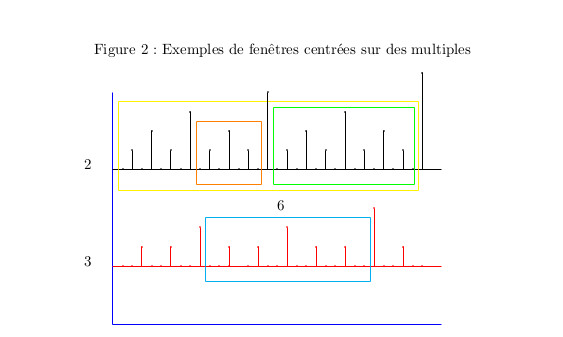
♥♥ 1.2.2006 : Fractales, symétrie et conjecture de Goldbach (6)

-
♥ 14.5.25 : Passage des matrices des décompositions de Goldbach aux pavages de Penrose

-
♥ 10.2.25 : Matrices de booléens de divisibilité, invariance, symétrie

-
♥ 8.2.25 : Une matrice qui grandit et fournit des décompositions de Goldbach

-
♥ 5.2.25 : Conjecture de Goldbach, matrices booléennes, symétries

-
♥ 5.5.25 : Revenir aux équations algébriques
 programmation du test du déterminant de la matrice de Sylvester des deux polynômes à considérer pour Goldbach (et son résultat) programmation du test du déterminant de la matrice de Sylvester des deux polynômes à considérer pour Goldbach (et son résultat)    
-
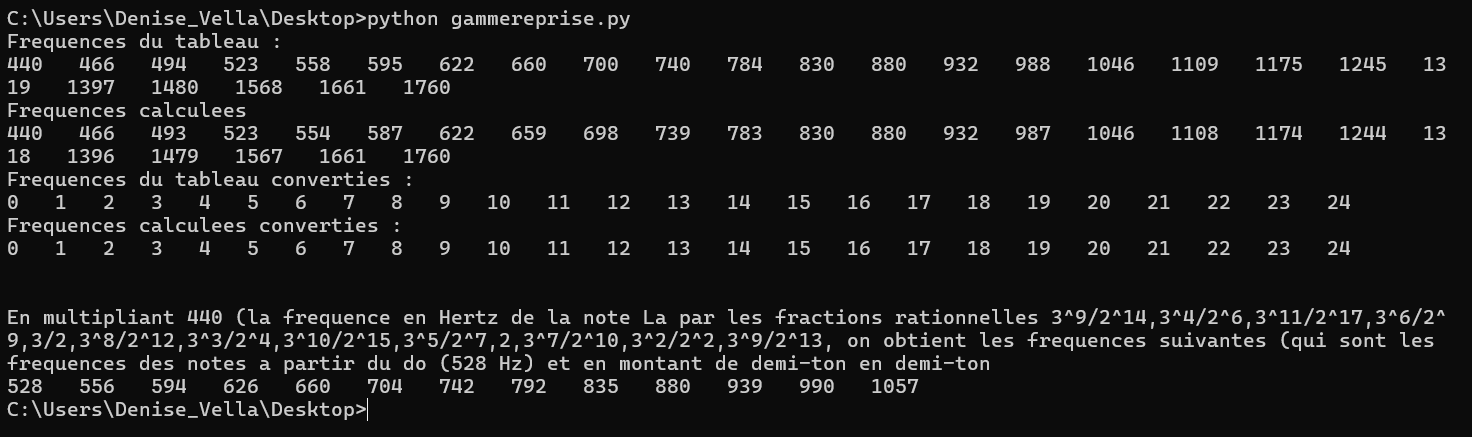
♥ avril 2025 : musique : conversion fréquences des notes, nombres entiers (origine la = 440 Hertz)
-
♥ 8.11.2024 : qui utilise des automorphismes intérieurs sans en avoir conscience

-
♥ 24.11.2024 : résumé des résultats dans le plan complexe (nombres-bases pour calc. rac. niemes)

-
♥ Octobre 2024 : opérateurs matriciels pour conjecture de Goldbach (776)

-
♥ un ensemble, une transformation, des traces de premiers (756)
-
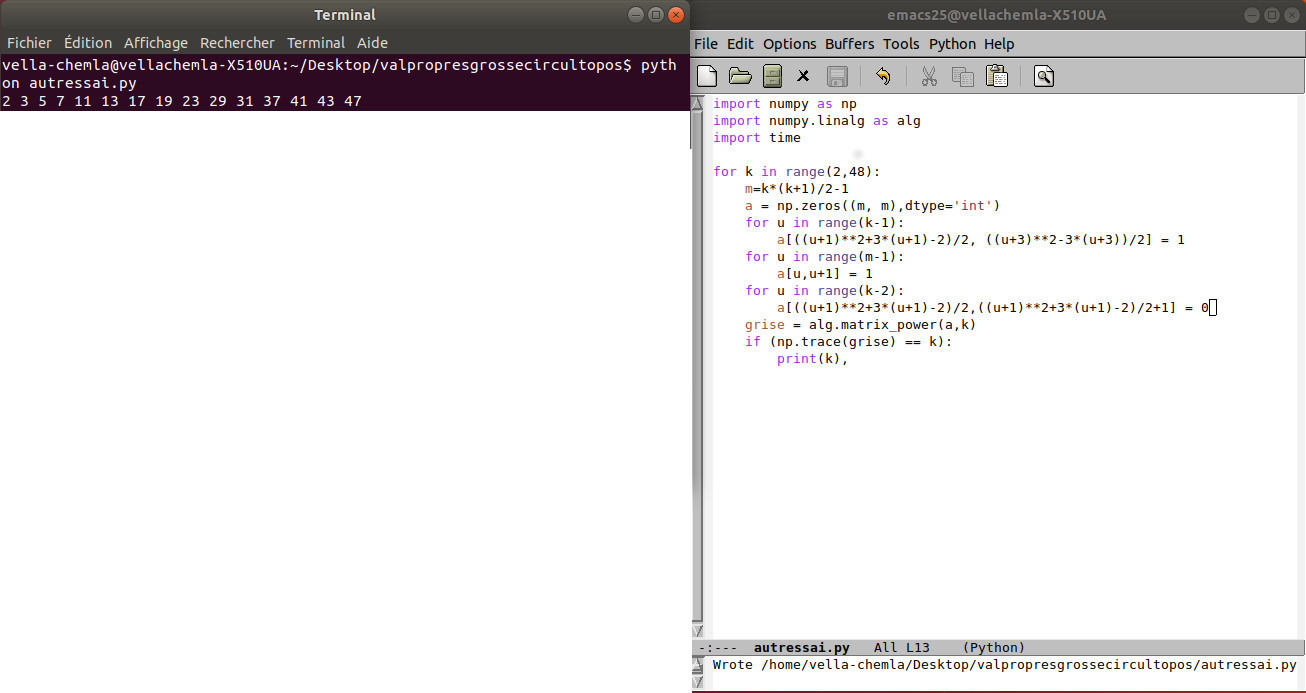
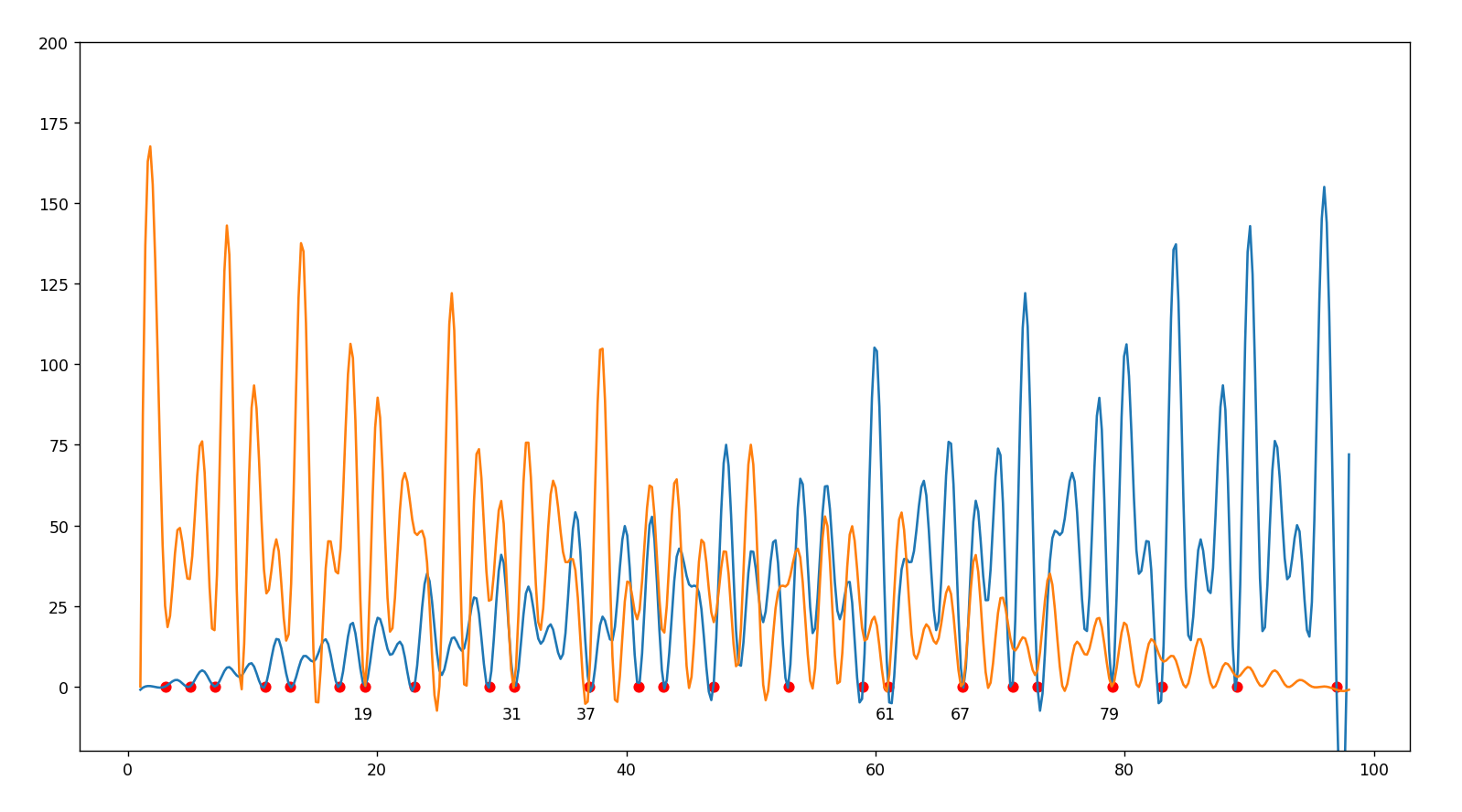
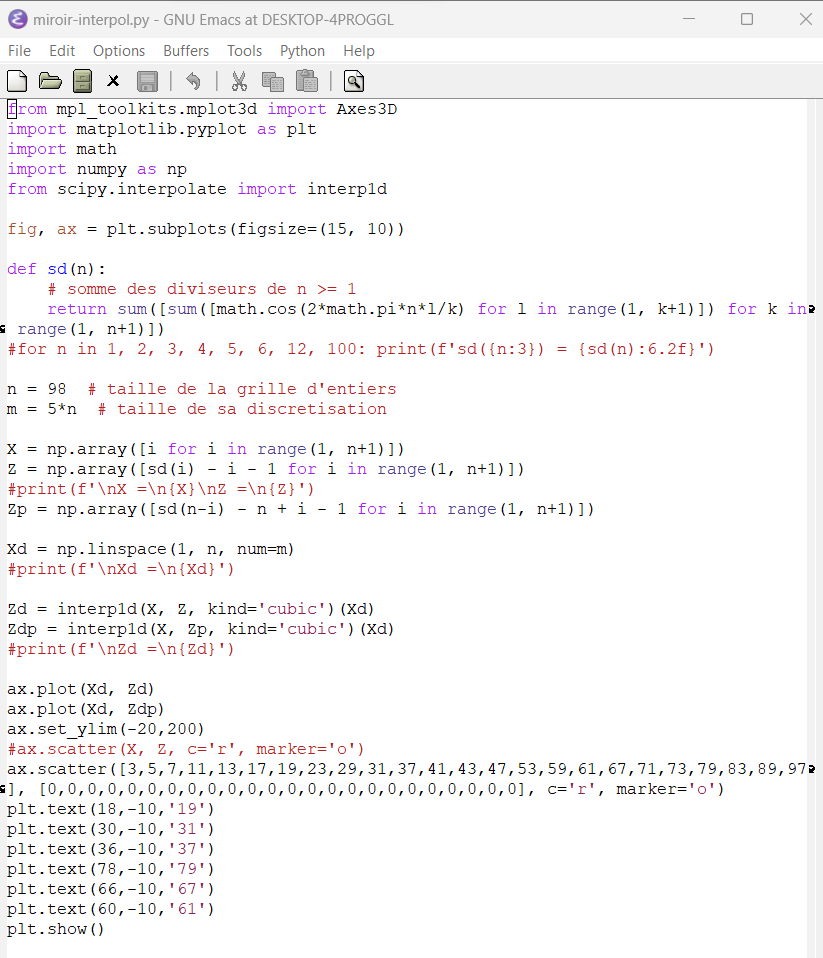
♥ juillet 2023 : une idée qui a fait son temps : on interpole la somme de somme de cos (qui s’annule pour les premiers) par une (smoothie !) cubique, on prend sa symétrique par rapport au milieu et on voit les points nuls communs qui sont les décomposants de Goldbach (729)
-
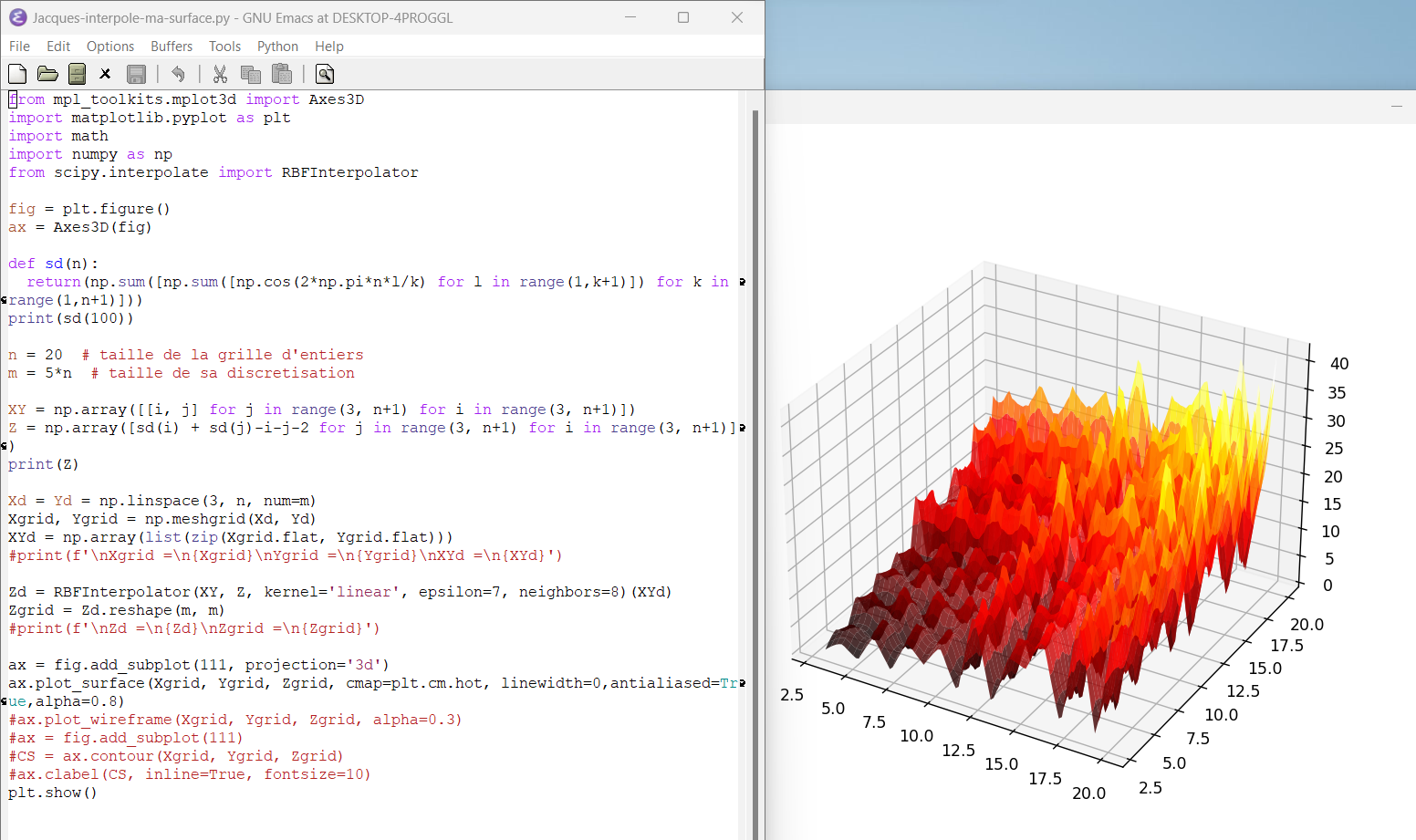
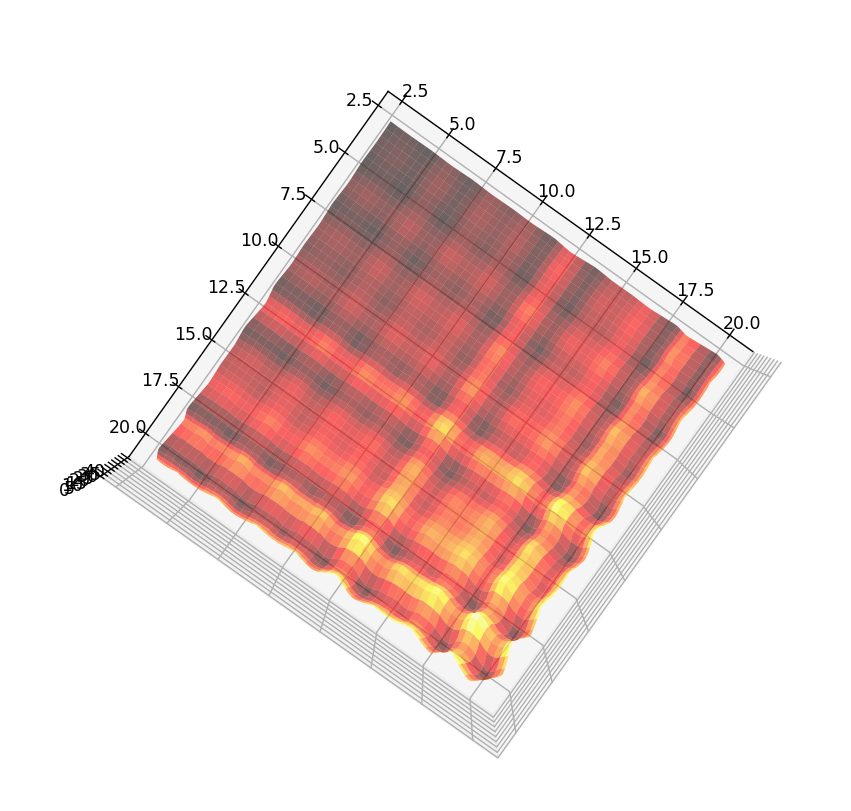
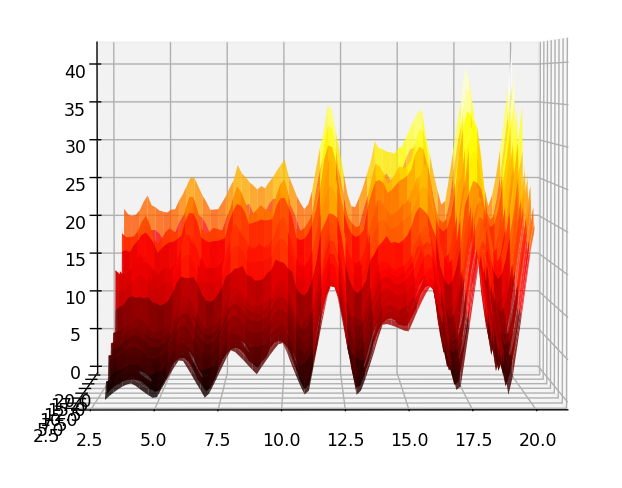
♥ juillet 2023 : graphique 1 : enfin ma surface bosselée avec les décompositions de Goldbach qui ’’tombent au sol’’ (z=0) en python, graphique 2 : Plaid Goldbach vu de dessus (on distingue en foncé 3+3, 3+5, 3+7), graphique 3 : les nombres premiers de 3 à 19 vus en coupe de profil de la surface bosselée et enfin, plaid 500 en python (727)
-
♥ janvier 2023 : Conjecture de Goldbach et logique propositionnelle (propositions à une variable) (699)
 (en) (en) 
-
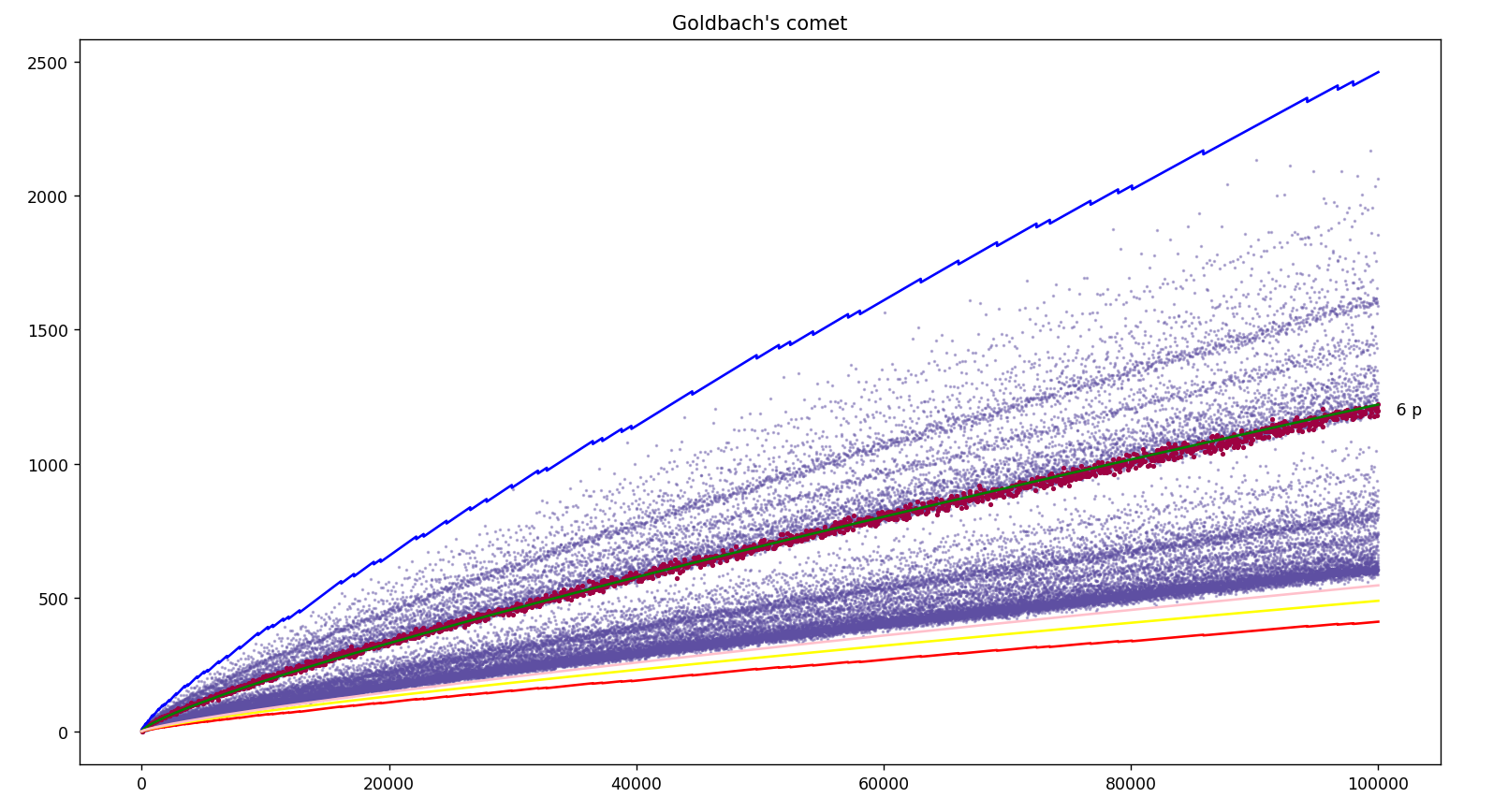
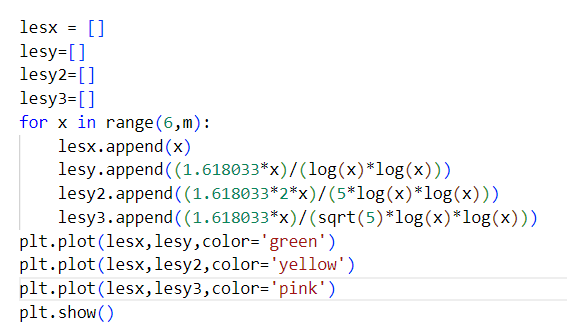
♥ 19.11.2022 : que le nombre d’or φ soit caché dans la comète des nombres de décompositions de Goldbach, ça devrait couler sous le sens ! (Les programmes sont la légende des courbes : la rouge (Prod(1-2/p).x/6, avec p premier < √x), la jaune (2φ.x/(5.log(x).log(x))) et la rose (φx/(√5.log(x).log(x))) semblent minorer la comète, la bleue semble la majorer (Prod(1-2/p).x, p premier < √x), et la verte φ.x/(log(x).log(x)) semble tomber pile au milieu des nombres de décompositions des pairs de la forme 6p, avec p premier).

-
♠ Décembre 2019 : Leila m’aide (598)

-
♠ 4.12.2019 : Aide de Leila Schneps (591)

-
♥ 29.4.2019 : compositions palindromiques (555)

-
♥ 12.7.2018 : palindromes (476)


-
♥ 1.8.2015 : Calculer l’indicateur d’Euler des nombres par un calcul matriciel (290)
 janv. 2026 janv. 2026 
-
♥ 29.7.2015 : Calculer les sommes de diviseurs par un calcul matriciel (288)
 janv. 2026 janv. 2026 
-
♥ 27.7.2015 : Matrices, sommes de diviseurs, produits de restes (287)

-
♥10.7.2014 : Primalité et zéros de sommes de cosinus (ou bien "elle c’est simple, je l’adore !", première rencontre) (258)

-
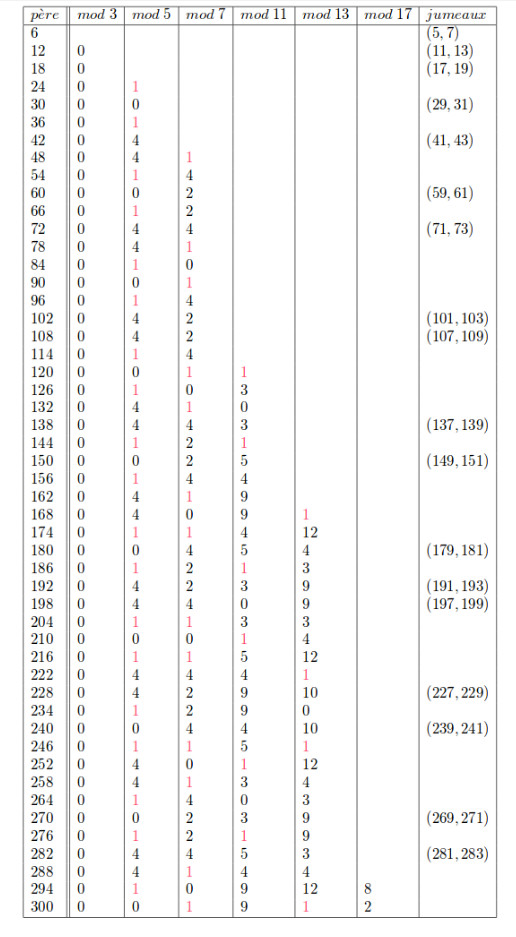
♥ 17.5.2014 : continuer de suivre Galois (ajout du problème des nombres premiers d’écart 2) (255)


-
♥ 23.12.2013 : Analogie (220)

-
♥ 1.1.2012 : Bonne année 2012... (143) (nullité déterminant matrice de Sylvester)

-
♥ 11.11.2011 : En attendant le 7 juin 2012 (les 270 ans de la conjecture de Goldbach), utiliser les équations algébriques pour trouver les décomposants de Goldbach... (135)

réétudié en mai 2025 :  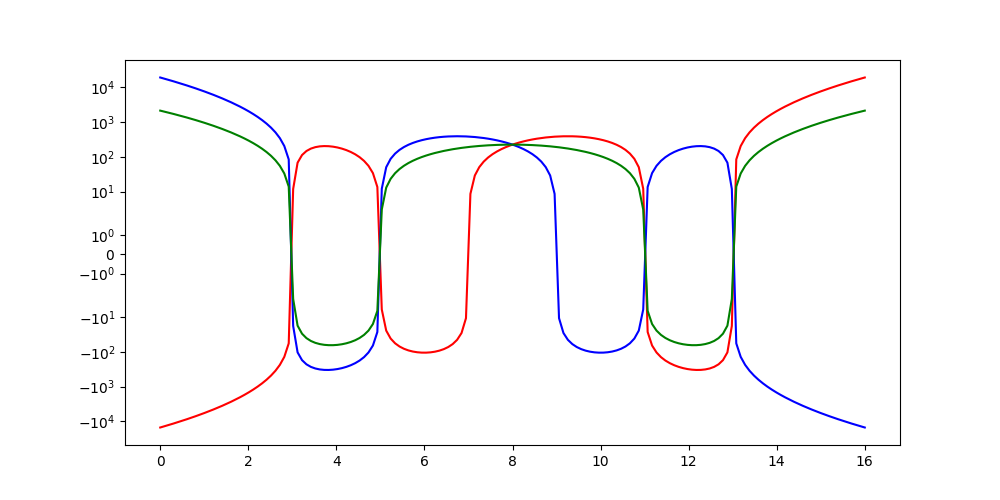 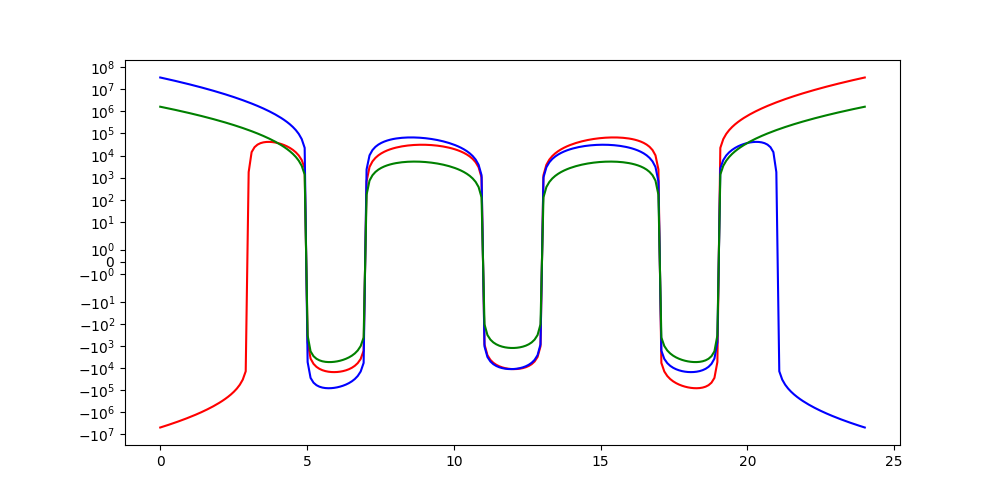
-
♥ 6.11.2011 : Une dernière idée : utiliser la théorie de Galois pour trouver les décomposants de Goldbach... (134)

-
♥ 31.10.2011 : Une dernière idée : utiliser la théorie de Galois pour trouver les décomposants de Goldbach... (133)

-
♦♦;-) à Daniel Diaz, qui a écrit gnu-prolog. (107)

-
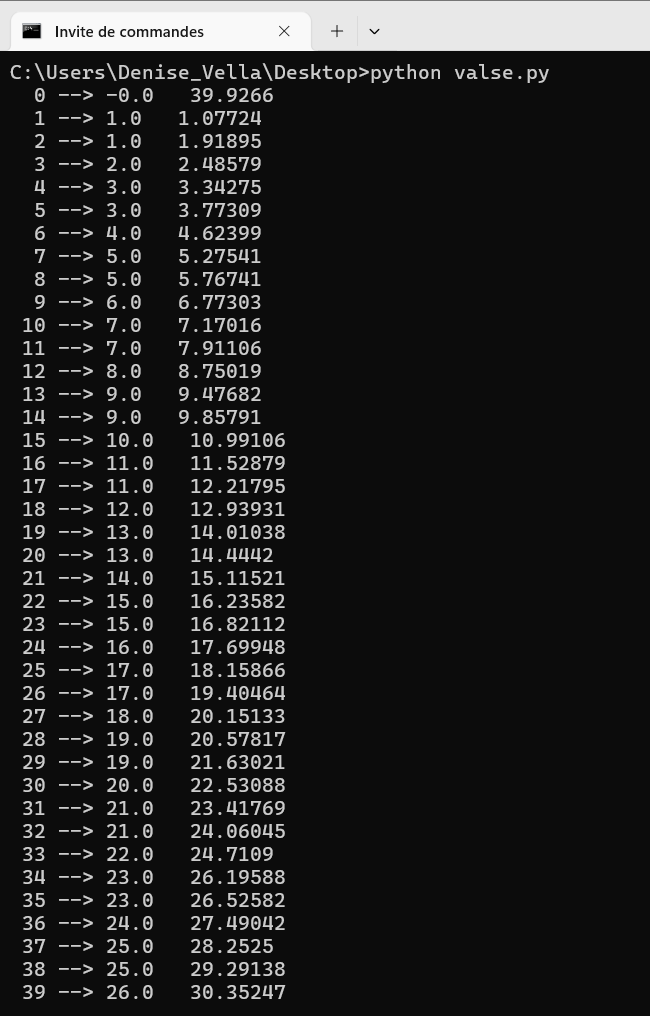
janvier 2026 : ose un début de valse, jusqu’à onze
-
Bonne année 2026 ! Je viens d’apprendre un truc : j’avais utilisé en février 2025 des matrices que je pensais symétriques pour représenter les décompositions de Goldbach. En fait, c’étaient des matrices qu’on dit "persymétriques", elles sont symétriques par rapport à "l’autre diagonale". Si je veux en faire des matrices auto-adjointes, il faut que j’inverse les lignes et les colonnes ; ça se fait facilement en python en prenant à la place de la matrice M la matrice M[::-1,::-1] (pour une matrice 2×2).
-
8.12.2025 : données chiffrées sur la représentation statistique des thésardes dans la base de données généalogique des mathématiques MGP en utilisant une liste des prénoms de l’Insee, féminisée par nombre le plus grand d’occurrences

-
7.8.2025 : carrés écossais et points fixes dans le plan complexe
 (en) (en)  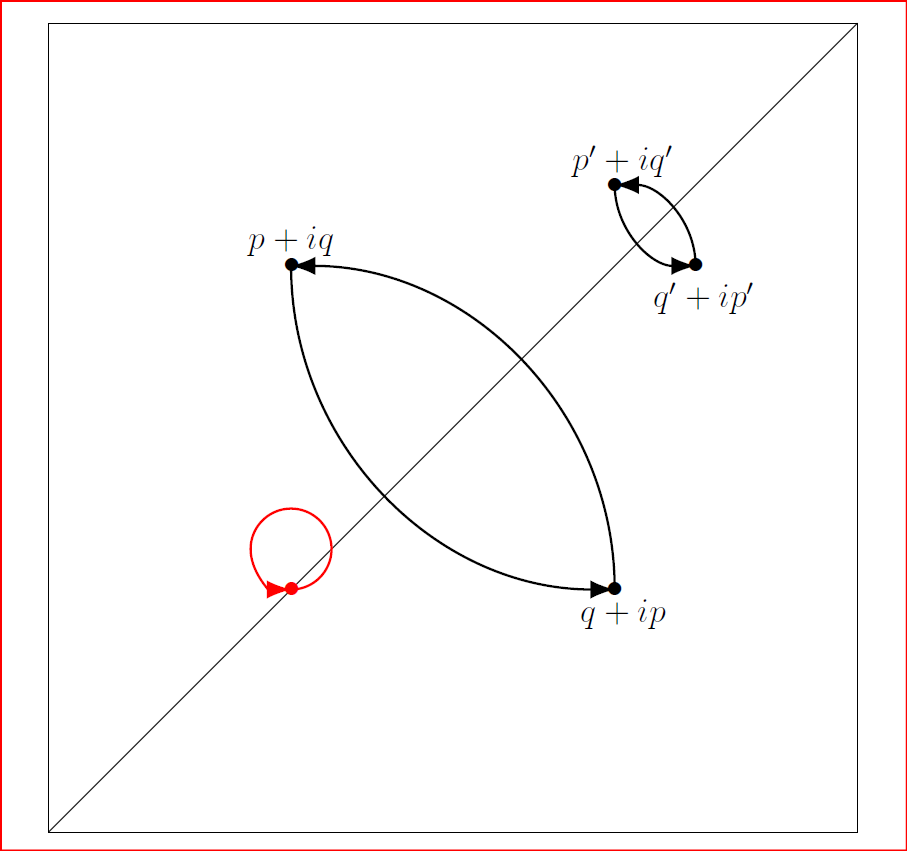
-
novembre 2025 : données chiffrées
 Traduction d’un article d’Allyn Jackson de 2007 au sujet de la base de données de généalogie mathématique de Harry Coonce Traduction d’un article d’Allyn Jackson de 2007 au sujet de la base de données de généalogie mathématique de Harry Coonce 
-
novembre 2025 : se détendre en déposant un brevet : le Planeprem

-
octobre 2025 : Jensen dans l’Intermédiaire des mathématiciens

-
août 2025 : carrés écossais et rotations dans le plan complexe

-
septembre 2025 : conjecture de Goldbach et entropie

-
octobre 2025 : jusqu’à 108, comparaison de la somme des inverses des nombres premiers jusqu’à x et de ln(ln x)

-
septembre 2025 : Inspirée par cette vidéo
 , on vérifie qu’on peut couper un entier en deux réels qui sont tels, chacun, qu’ajouté à leur inverse, ils donnent l’entier en question. Les réels dont la somme est égale à l’entier sont de la forme 0.5(k ± √ (k^2-4)). , on vérifie qu’on peut couper un entier en deux réels qui sont tels, chacun, qu’ajouté à leur inverse, ils donnent l’entier en question. Les réels dont la somme est égale à l’entier sont de la forme 0.5(k ± √ (k^2-4)).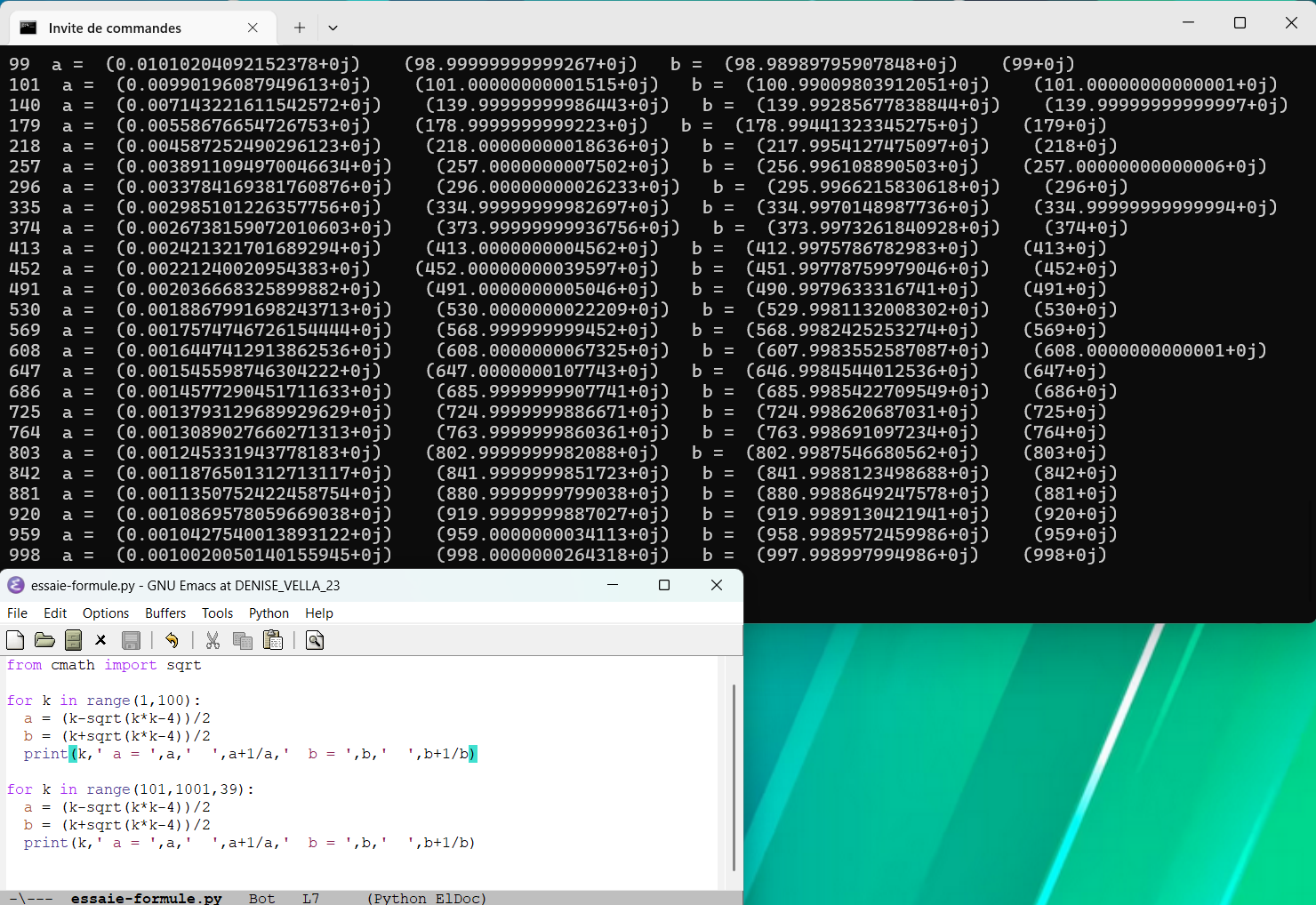
-
septembre 2025 : lien φ π étonnant
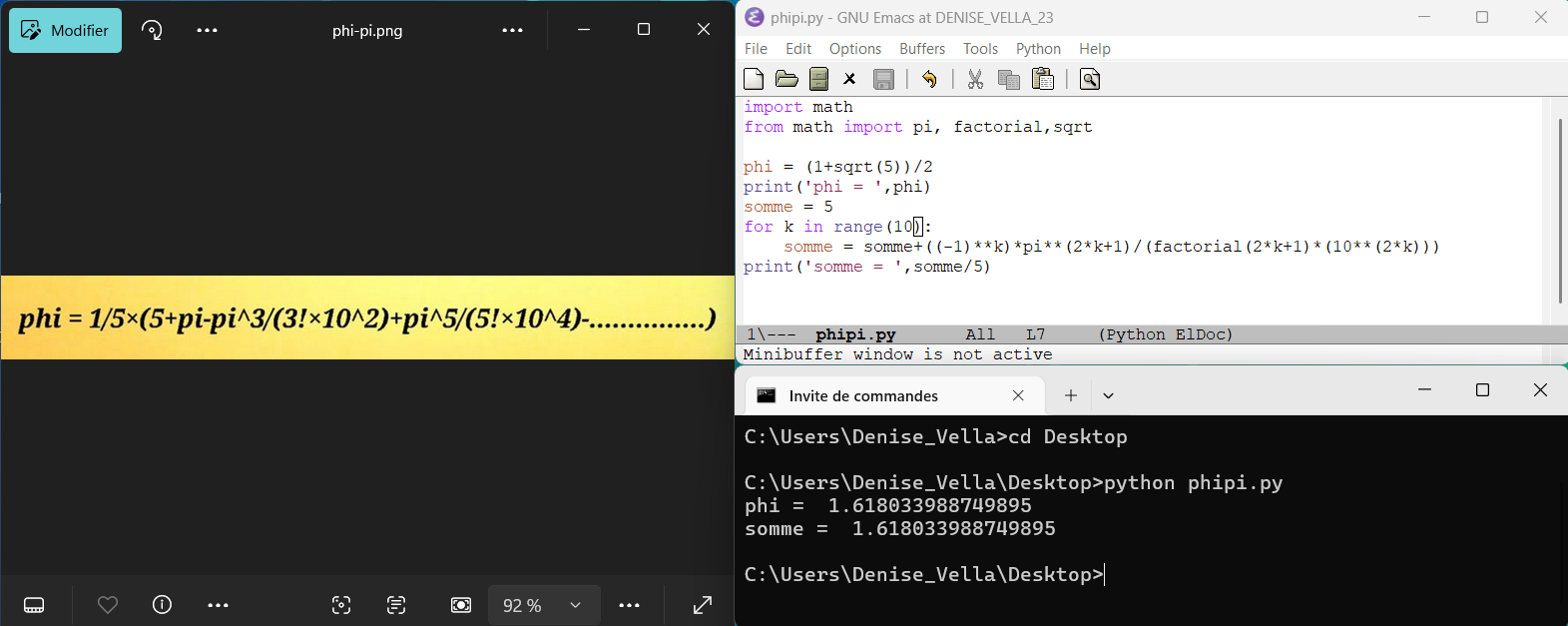
-
correction : Euclide et écart 2 entre deux nombres premiers
 (en) (en) 
-
septembre 2025 : revenir à la somme des résidus quadratiques égale à √n ou bien i √n, transcription d’un article de Dirichlet et deux traductions afférentes
 résumé au sujet des sommes quadratiques de Gauss résumé au sujet des sommes quadratiques de Gauss 
-
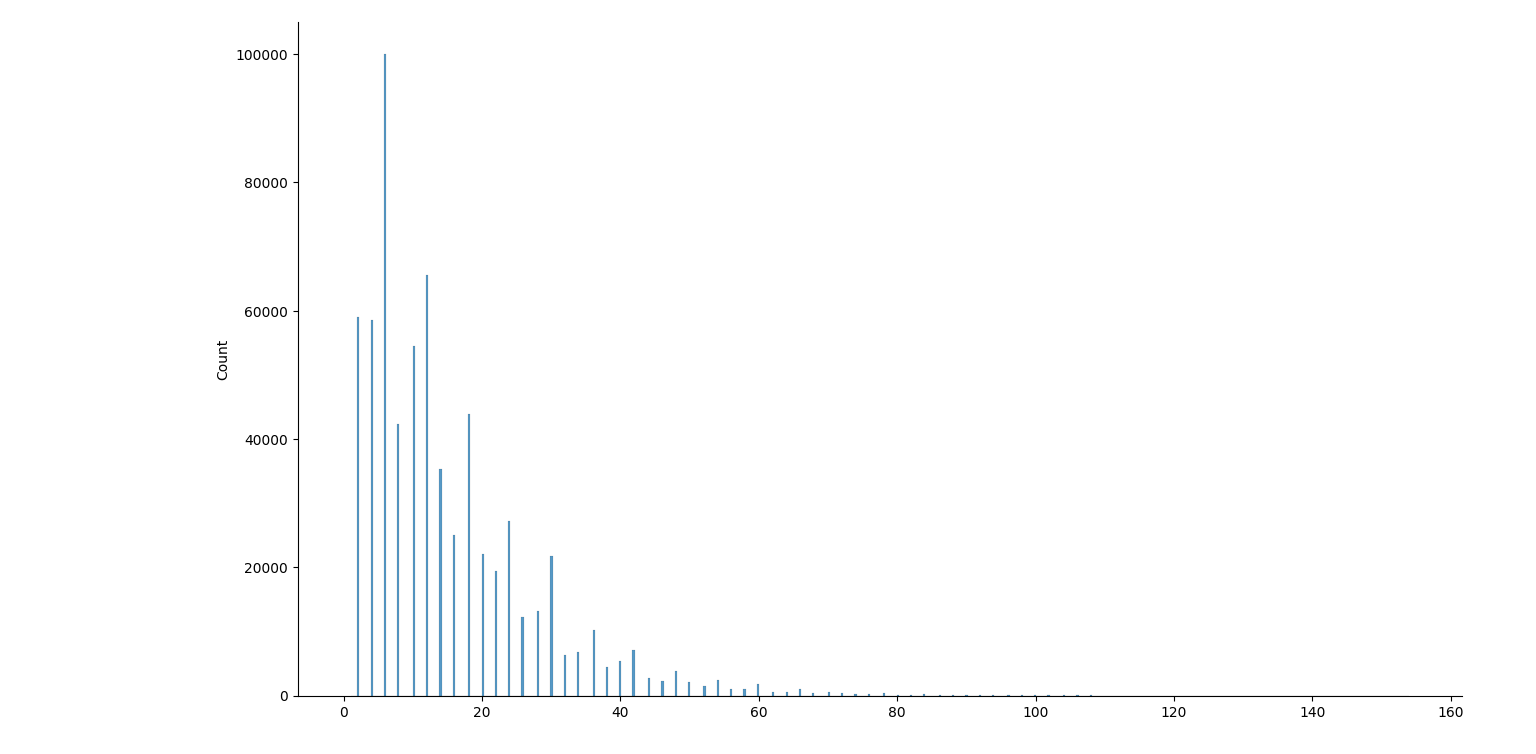
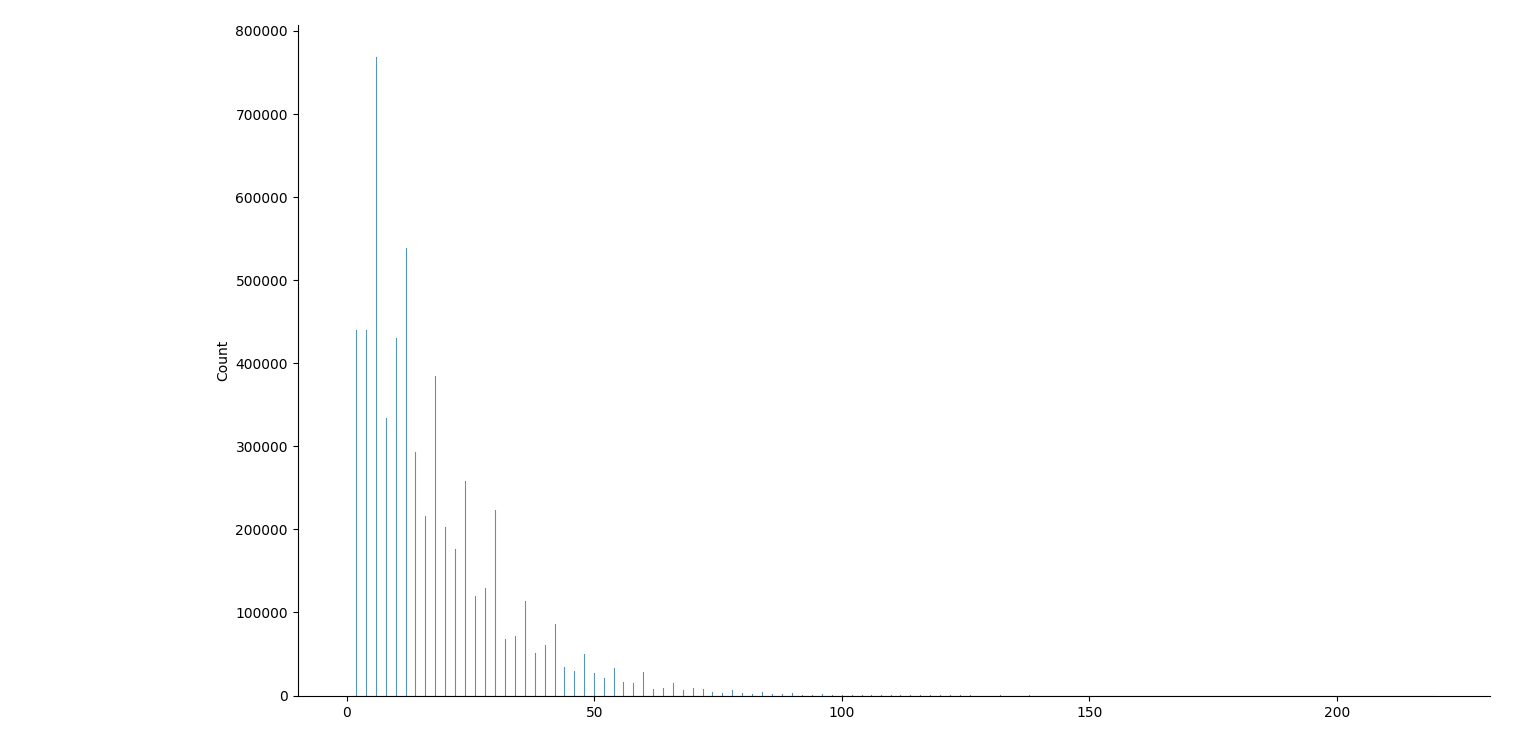
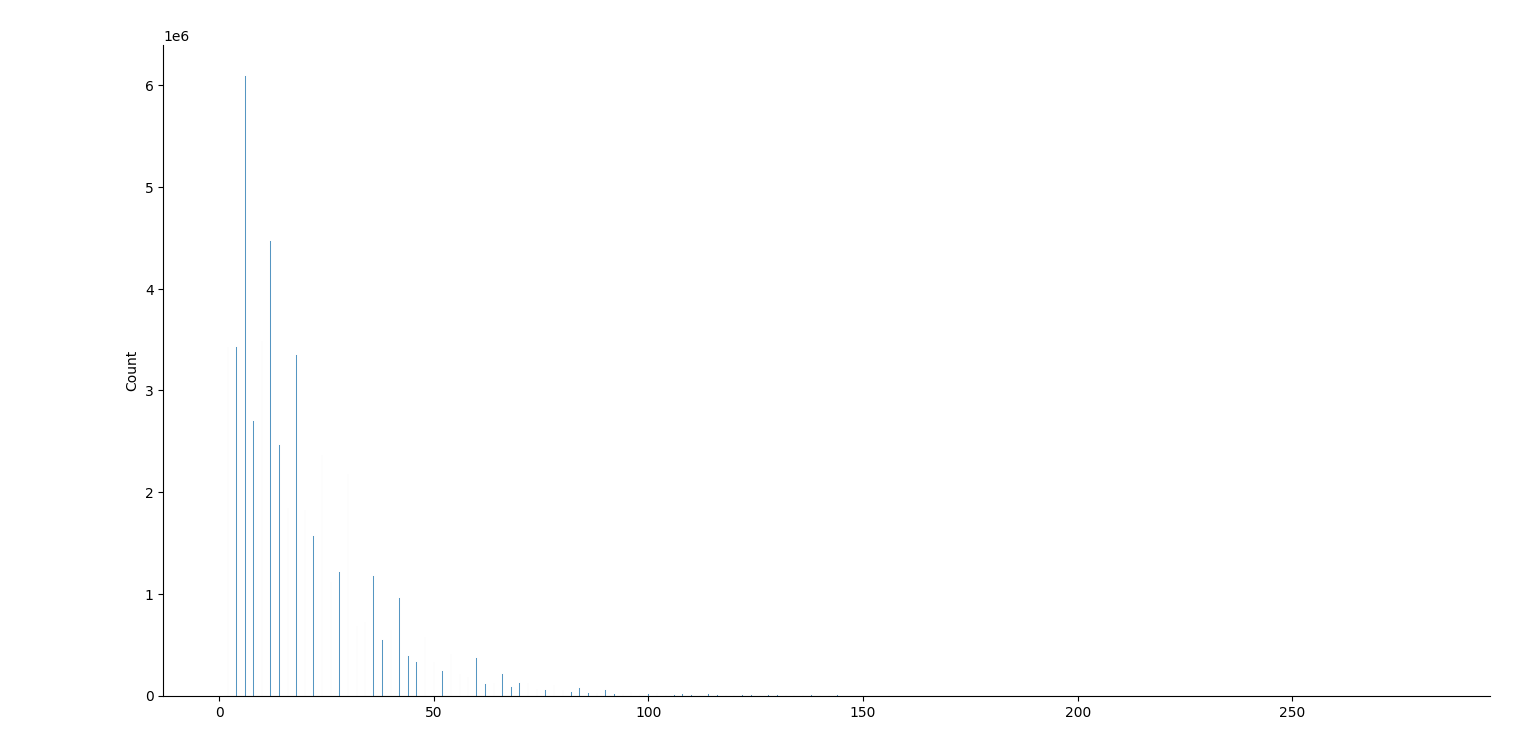
août 2025 : prime gaps : écarts entre deux nombres premiers successifs, histogrammes pour les nombres premiers jusqu’à 106, jusqu’à 107, jusqu’à 108, jusqu’à 109 (des manques dans ce dernier graphique, le package seaborn a du mal)
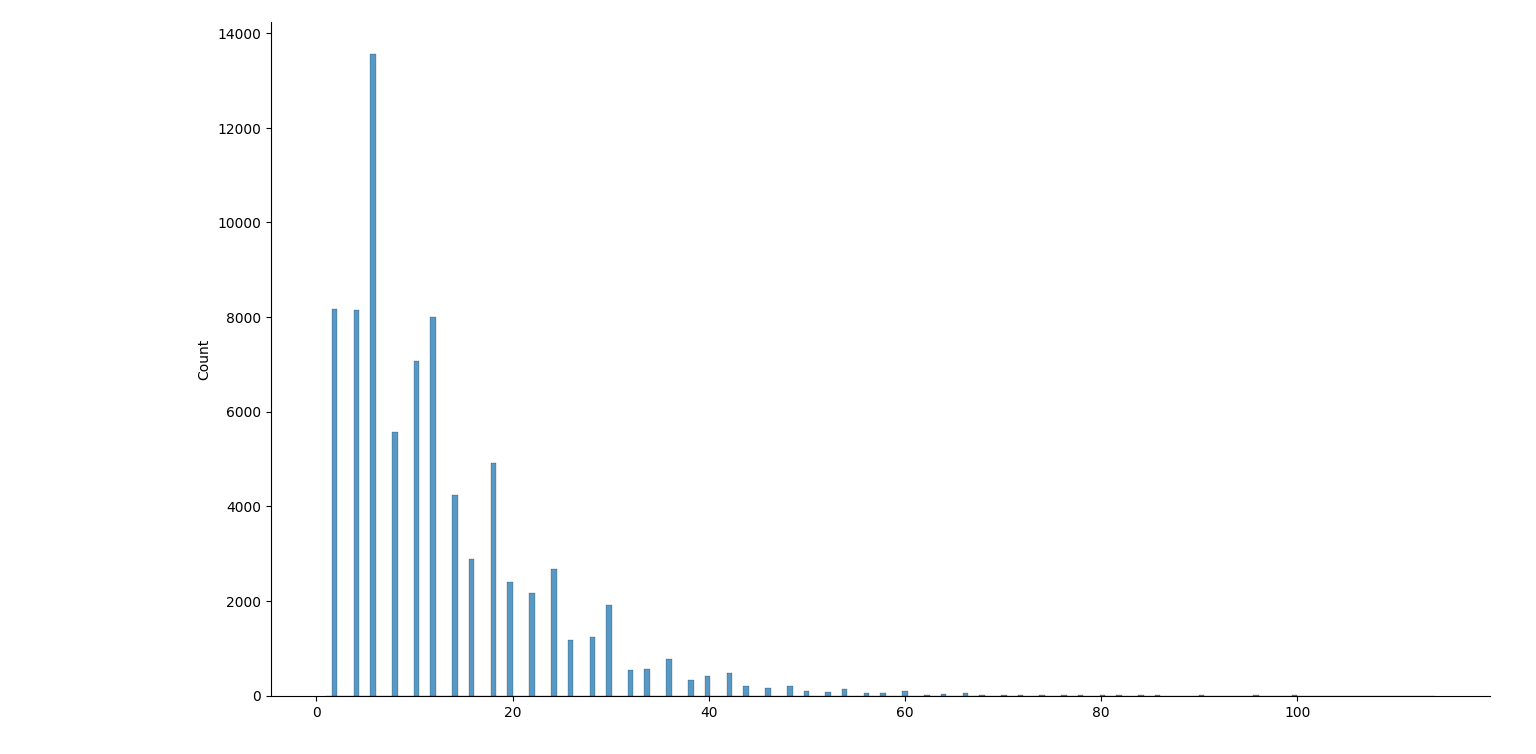   
-
août 2025 : toutes les notes au format pdf
    la bibliographie au format pdf la bibliographie au format pdf 
-
août 2025 : j’ai fait le tour

-
juillet 2025 : raccourci fatalement faux

-
juillet 2025 : carrés simples
 avec la relation non résidu quadratique de annotée, parce que ces dessins font penser à la démonstration géométrique d’Eisenstein de la loi de réciprocité quadratique (voir avec la relation non résidu quadratique de annotée, parce que ces dessins font penser à la démonstration géométrique d’Eisenstein de la loi de réciprocité quadratique (voir  ) )  résultat d’exécution résultat d’exécution  sans RQ sans RQ 
tables de multiplication dans ℤ/nℤ 
-
juillet 2025 : multiplication par i
 conclusion : ça ne va pas, il y a plein de nombres pairs dont aucun point ne se projette sur la diagonale, mauvaise idée. conclusion : ça ne va pas, il y a plein de nombres pairs dont aucun point ne se projette sur la diagonale, mauvaise idée.
-
18 juillet 2025 : carrés de chocolat inégaux, avec plein de petits rectangles ab ≠ ba un peu partout (parce qu’après tout, même si ça fait 12 feutres, 4 paquets de 3 feutres, ça reste différent de 3 paquets de 4 feutres)

-
juillet 2025 : Gerris (ce sont ces araignées d’eau à 4 pattes qui marchent sur l’eau)
 
-
juillet 2025 : mon carquois : je ne sais pas s’ils m’emmeneront quelque part mais j’aime bien ces dessins
  
-
Les délices des raisonnements discrets : traduction d’un texte de S. W. Golomb

-
Gauche ou droite, un extrait de G. Gamow

-
16.6.2025 : ou exclusif
 simplification : on oublie la symétrisation de la matrice, et le ou exclusif, on regarde simplement les points dont les coordonnées ne commutent pas simplification : on oublie la symétrisation de la matrice, et le ou exclusif, on regarde simplement les points dont les coordonnées ne commutent pas  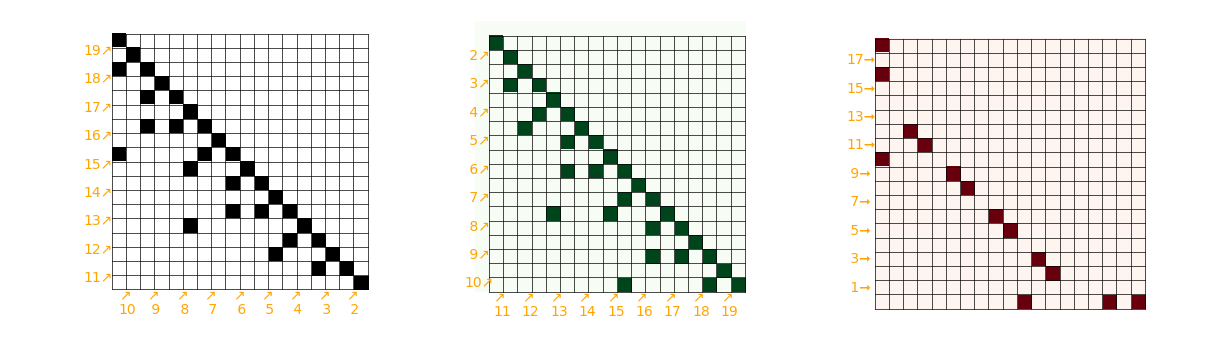 petit livret petit livret 
-
juin 2025 : plusieurs dessins par règles de réécritures de Lindenmayer en LaTeX Tikz
 
-
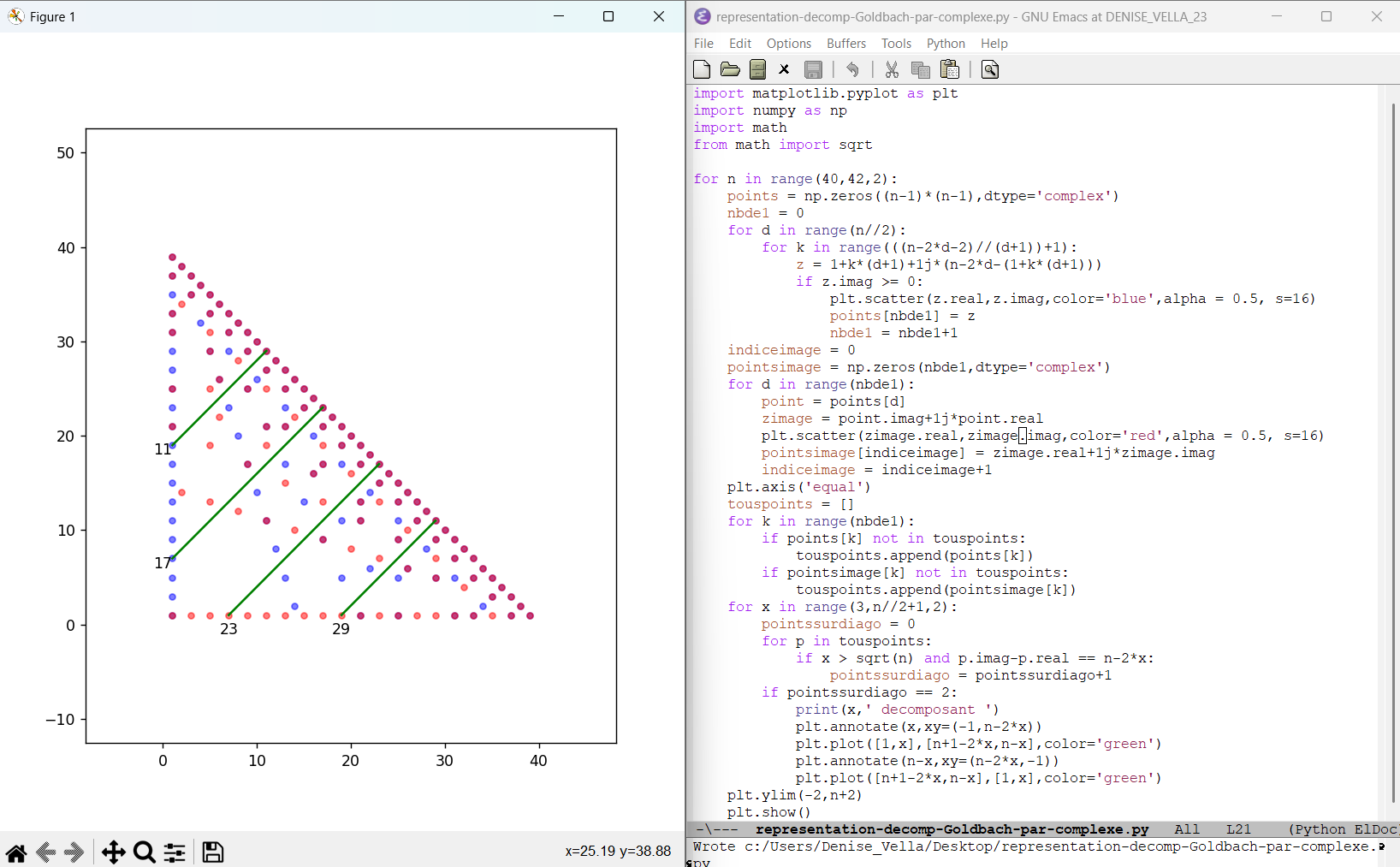
juin 2025 : décomposants de Goldbach en géométrie du plan complexe
-
juin 2025 : l’ensemble de la castafiore
 ensembles de Cantor ensembles de Cantor  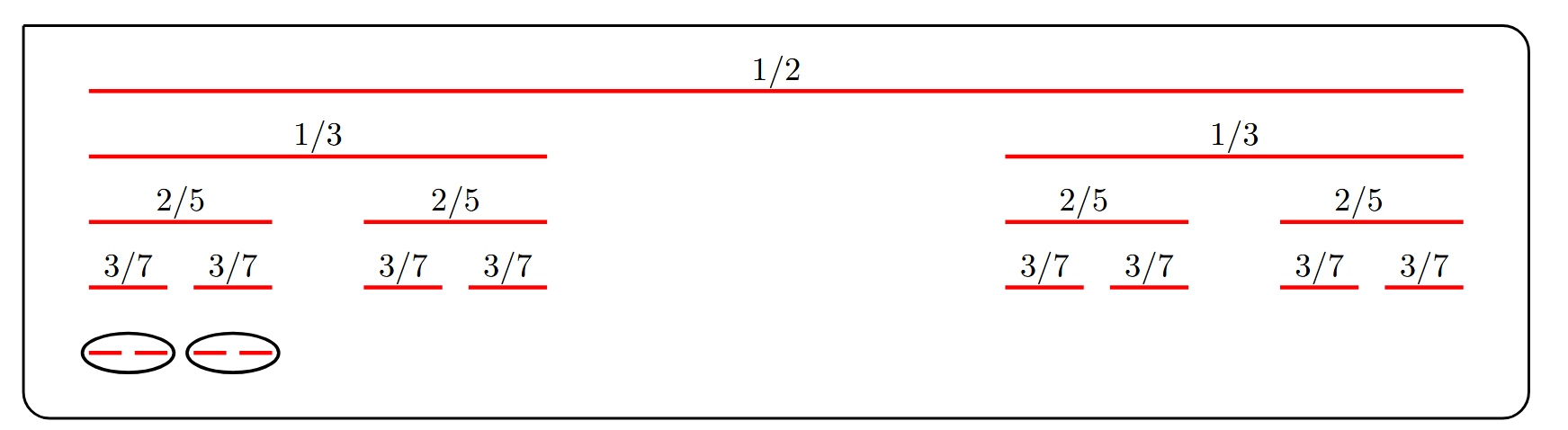
Chercher à obtenir l’ensemble de la castafiore en utilisant les programmes de l’été 2023 de dessin de fractals par expansion de polynômes  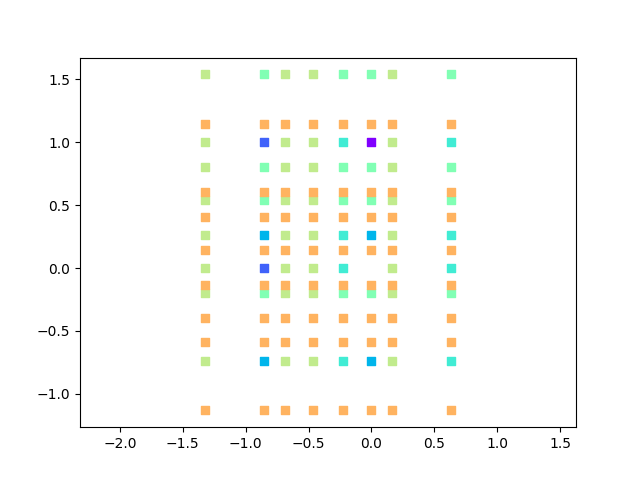 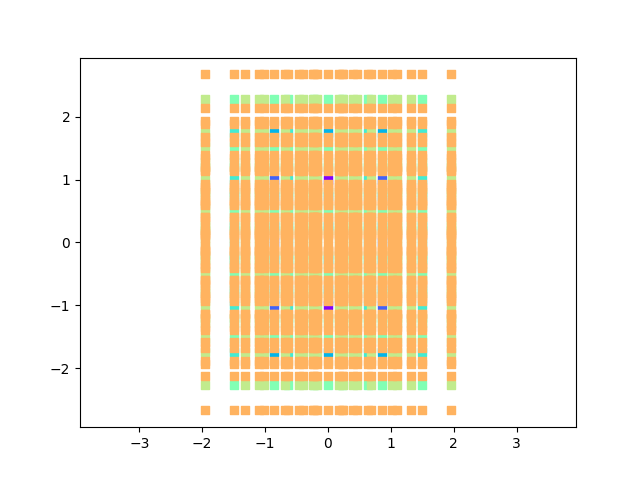 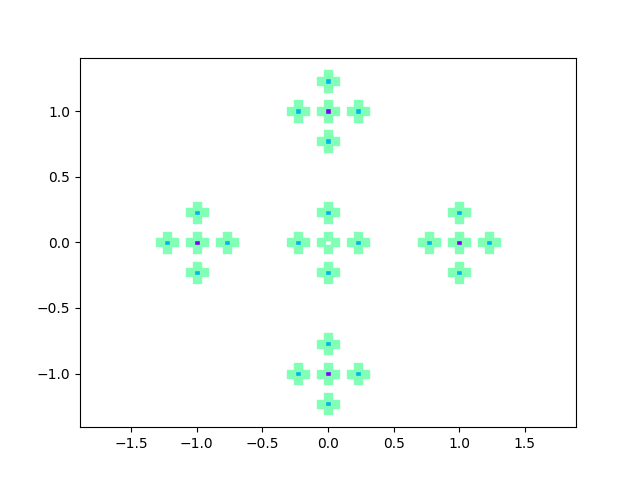
-
juin 2025 : donne du fil à retordre : Pavage de Ammann-Beenker dit "substitutions A5"

-
3.6.2025 : matrices recherchent invariants, désespérément
 petit livret des matrices or petit livret des matrices or 
-
29.5.2025 : Tout s’est écroulé, en mettant bien mes matrices à l’endroit sur le conseil d’une personne pleine de logique

-
♥ 14.5.25 : Passage des matrices des décompositions de Goldbach aux pavages de Penrose

-
mai 2025 : Très constantes

-
petit memo pour φ
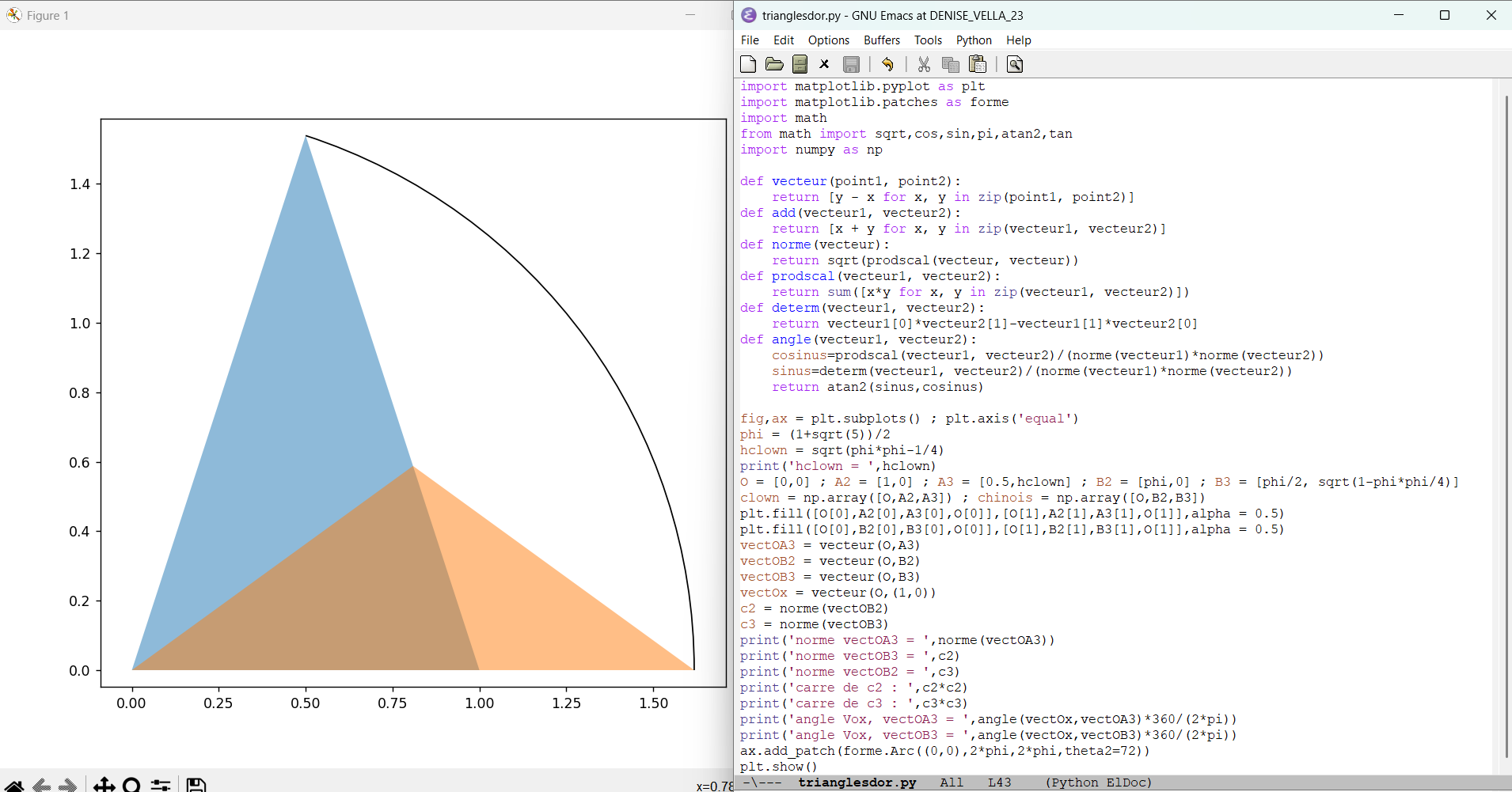
et illustration de ce que sont des pavages périodiques avec des tuiles de même forme mais de plus en plus grosses 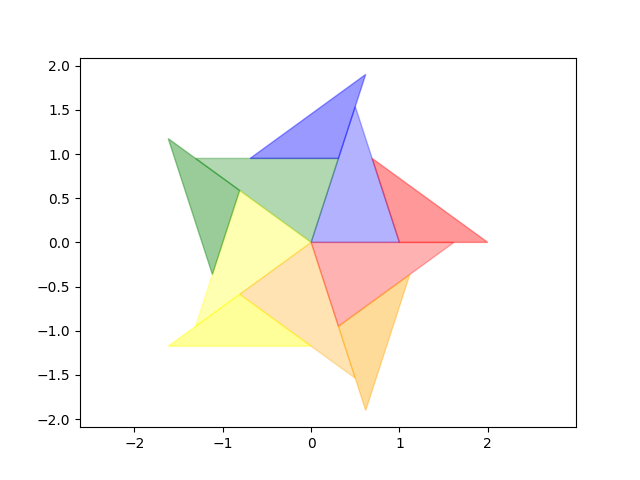 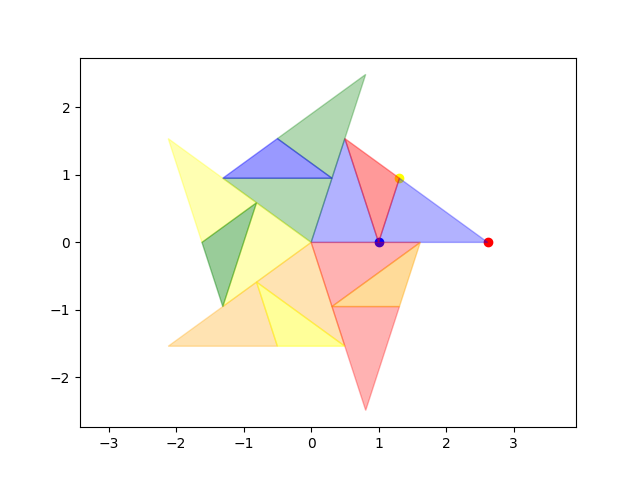 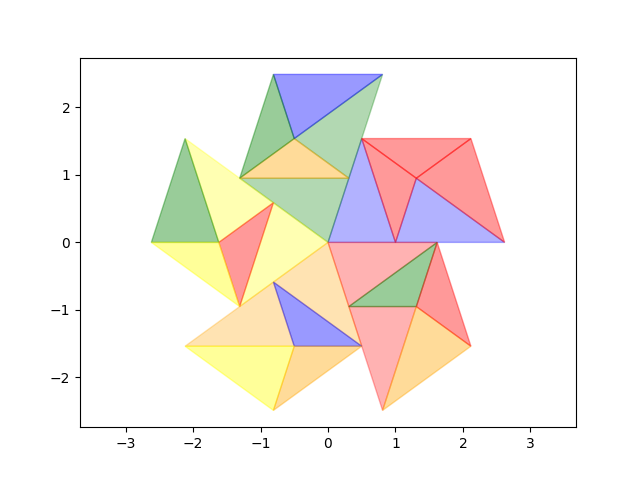  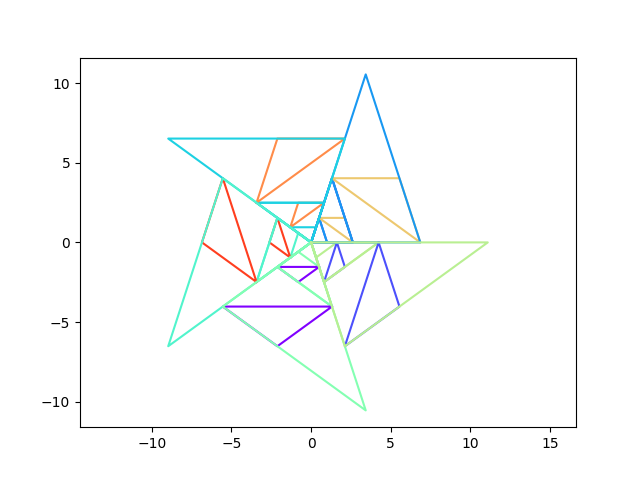 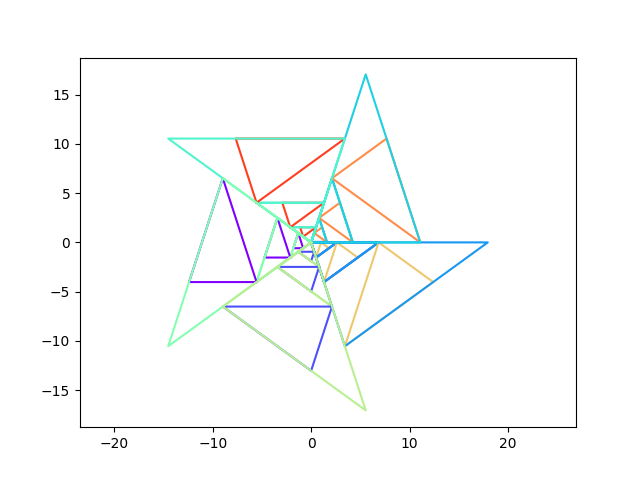
On a essayé de montrer, par la couleur sur l’une des images, une sorte de bande de papier triangulaire infinie d’angle 36° et qu&rsuqo;on plierait sur elle-même en alternant le sens une fois sur deux ...
-
♥ 10.2.25 : Matrices de booléens de divisibilité, invariance, symétrie

-
♥ 8.2.25 : Une matrice qui grandit et fournit des décompositions de Goldbach

-
♥ 5.2.25 : Conjecture de Goldbach, matrices booléennes, symétries

-
mai 2025 : s’essayer à programmer les pavages de Penrose en python et traductions d’extraits de Noncommutative geometry à ce sujet
 
-
mai 2025 : correspondance ouïe-vue
 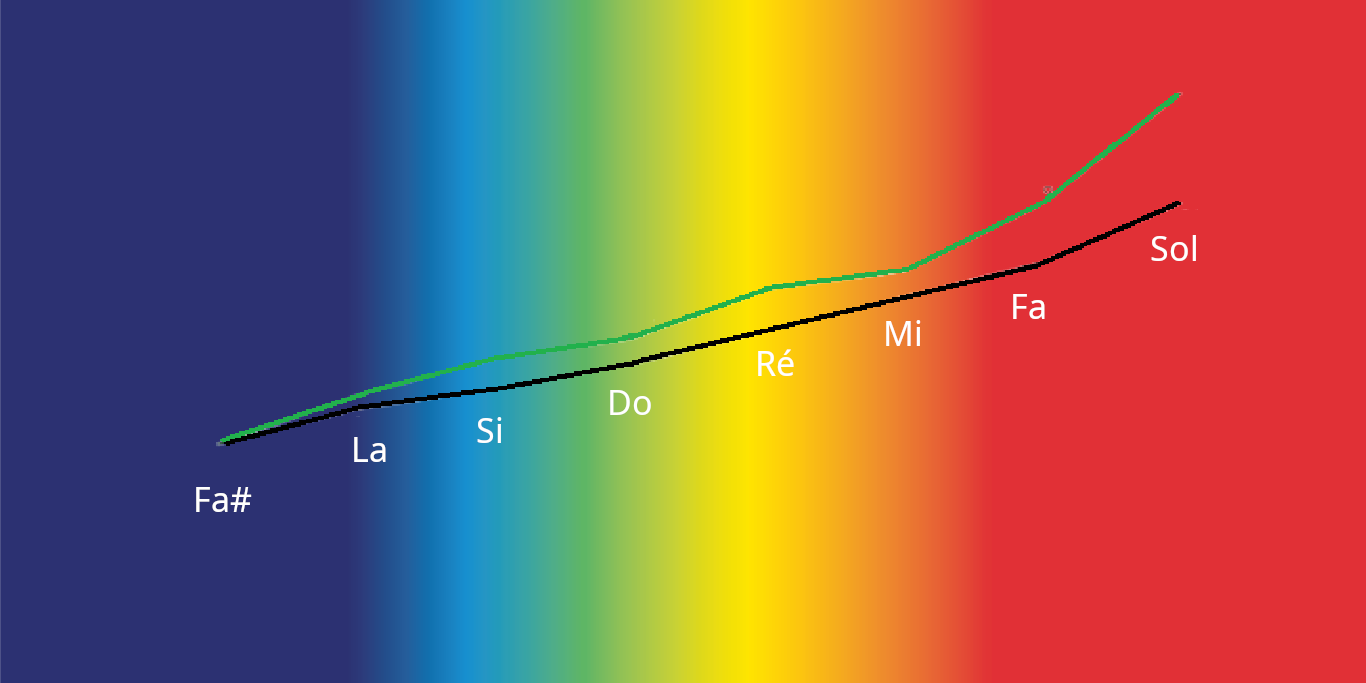
-
♥ 5.5.25 : Revenir aux équations algébriques
 programmation du test du déterminant de la matrice de Sylvester des deux polynômes à considérer pour Goldbach (et son résultat) programmation du test du déterminant de la matrice de Sylvester des deux polynômes à considérer pour Goldbach (et son résultat)    
-
mai 2025 : la première colonne de l’exponentielle d’une matrice de booléens détectant les seuls diviseurs propres fournit la primalité
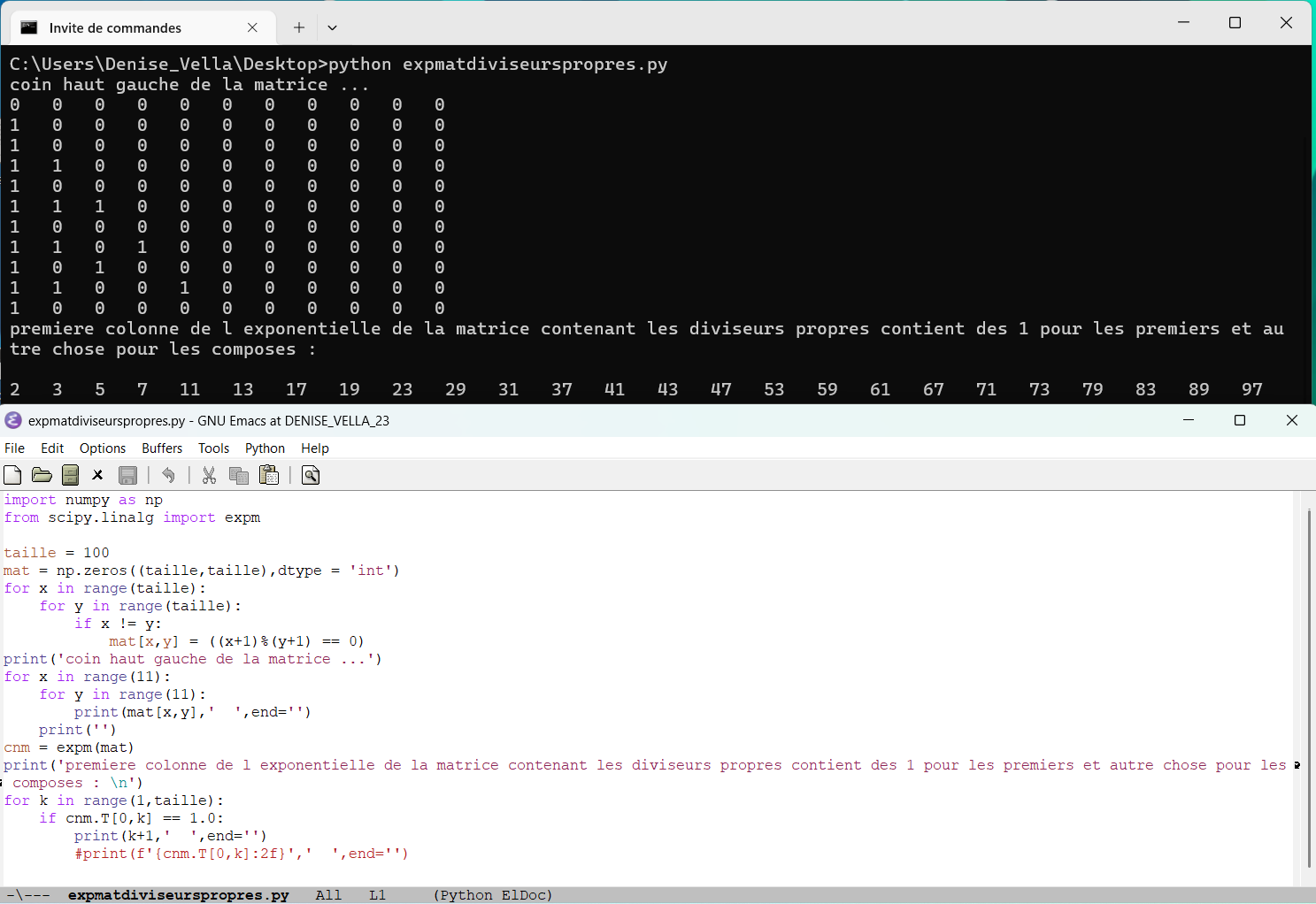
-
♥ avril 2025 : musique : conversion fréquences des notes, nombres entiers (origine la = 440 Hertz)
  
-
mai 2025 : petit retour aux polyèdres

-
Traduction du chapitre Groupe euclidien de Frank Morley

-
avril 2025 : bien comprendre la non-commutativité du langage : Transcription de Voyage autour du monde (extrait du livre Avec des nombres et des lignes d’André Sainte-Laguë)
 programmation de l’icosion et solutions programmation de l’icosion et solutions       
-
avril 2025 : racines cubiques de l’unité et décomposants de Goldbach
 Sauter à pieds joints sur les calculs, c’est sûr qu’il faudrait y parvenir, parce que très vite, ou même très, très vite... Sauter à pieds joints sur les calculs, c’est sûr qu’il faudrait y parvenir, parce que très vite, ou même très, très vite... 
-
avril 2025 : traduction de l’article de Claude Chevalley : L’arithmétique dans les algèbres simples

-
avril 2025 : traduction de la note de Jacques Herbrand : Sur la non-contradiction de l’arithmétique

-
avril 2025 : transcription de l’article d’André Lentin : Équations dans les monoïdes libres
 (André Lentin est un mathématicien, logicien et informaticien théoricien français né le 9.11.1913 à Médéa en Algérie et mort le 9.1.2015 dans le 15e arrondissement de Paris. Son article est à mettre en lien avec le petit livre de Trahtenbrot (Algorithmes et machines à calculer) que m’avait offert Yves Césari, mon professeur d’Algorithmique, alors que j’étais en seconde année de Deug Mathématiques appliquées et Sciences sociales, à l’Université Paul Valéry de Montpellier, et dont on trouvera les scans du chapitre Le problème des mots dans la page de Notes.) (André Lentin est un mathématicien, logicien et informaticien théoricien français né le 9.11.1913 à Médéa en Algérie et mort le 9.1.2015 dans le 15e arrondissement de Paris. Son article est à mettre en lien avec le petit livre de Trahtenbrot (Algorithmes et machines à calculer) que m’avait offert Yves Césari, mon professeur d’Algorithmique, alors que j’étais en seconde année de Deug Mathématiques appliquées et Sciences sociales, à l’Université Paul Valéry de Montpellier, et dont on trouvera les scans du chapitre Le problème des mots dans la page de Notes.)
-
H. Cartan : Sur le fondement logique des mathématiques

-
avril 2025 : traduction d’une note de W. Quine : Concatenation as a basis for arithmetic (1946)

-
avril 2025 : traduction d’une note de J.A. Erdos : Sur les produits d’idempotents

-
22.4.2025 :

-
Regarder toutes les images

-
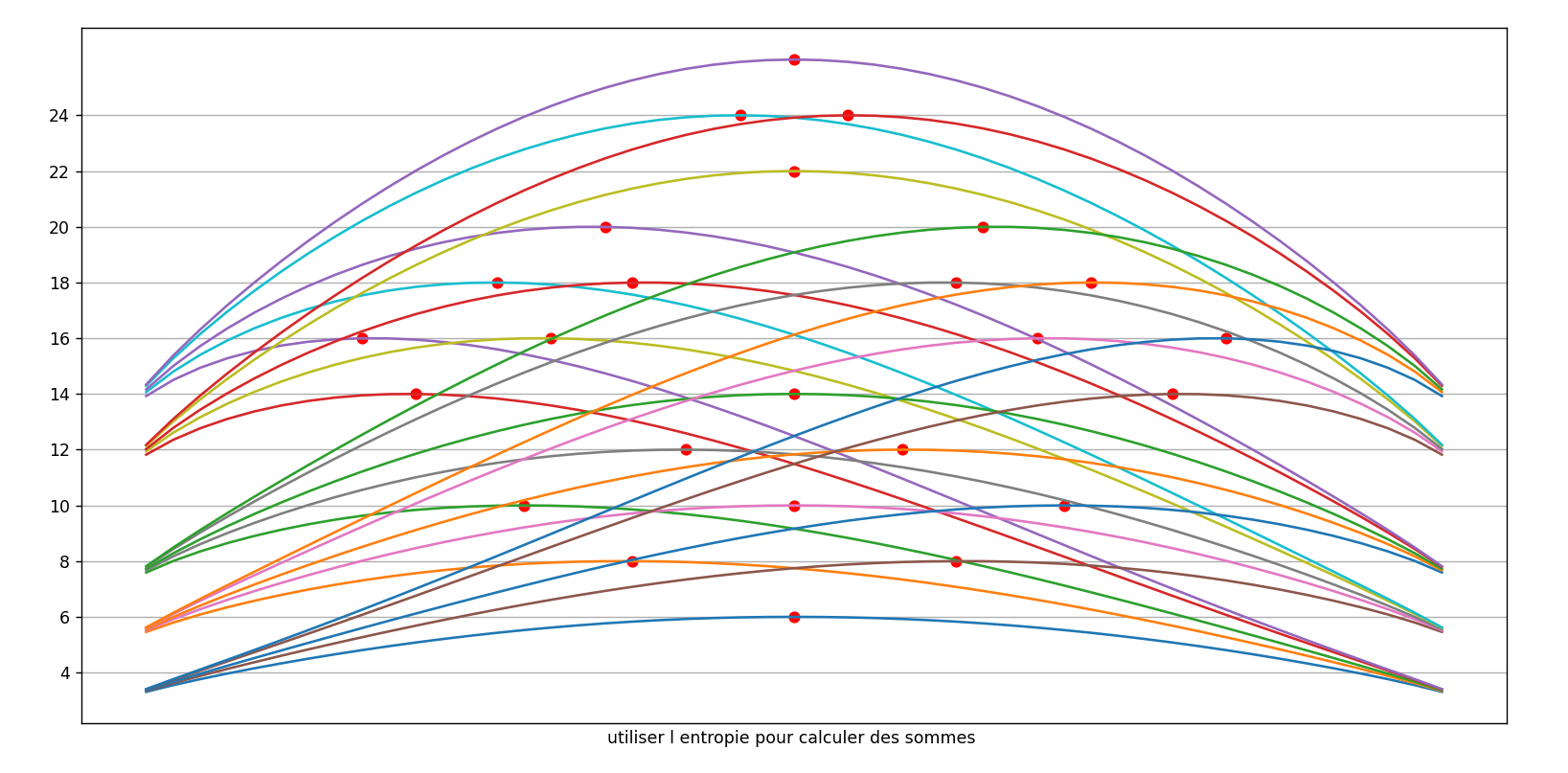
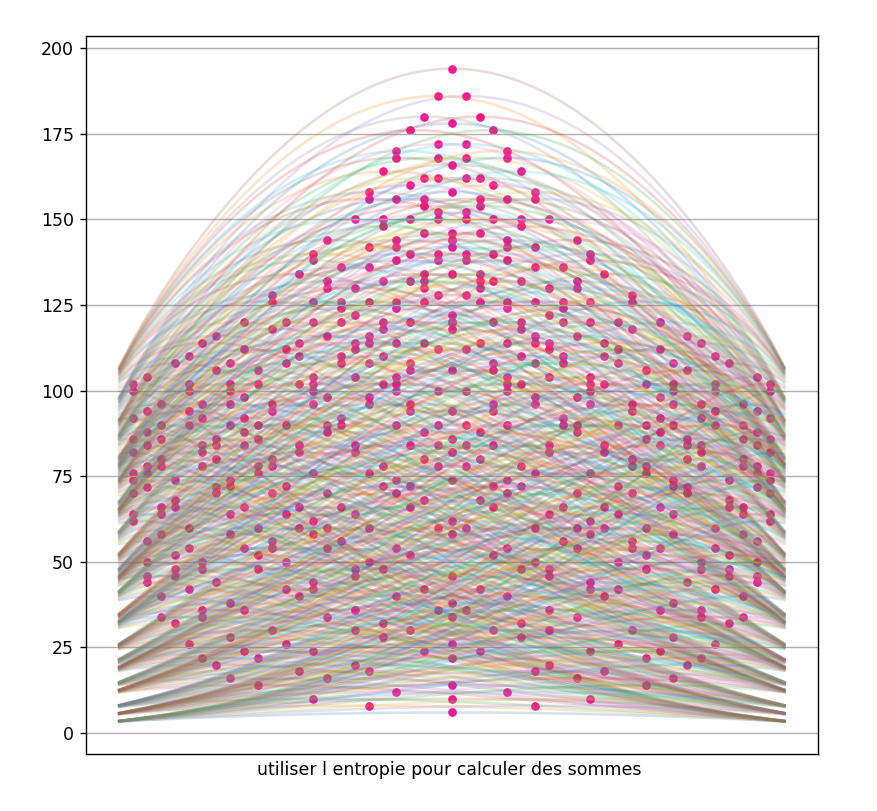
25.2.25 : L’ancien maillage que j’avais mis au jour en 2005 (voir aux pages ici et là) peut s’obtenir en calculant des sommes par utilisation de l’entropie de Shannon, entropie intervenant également en physique, ça fait plaisir ! Voici le programme utilisé pour obtenir les maximum "scatterisés" par python ci-dessous (on voit très bien 26=13+13, 24=11+13=13+11, etc.) :
 Traduction d’une référence de Maxim Kontsevich cité par Alain Connes Traduction d’une référence de Maxim Kontsevich cité par Alain Connes 
-
8.3.25 : programmer la conjecture de Mertens (100 et 1000)
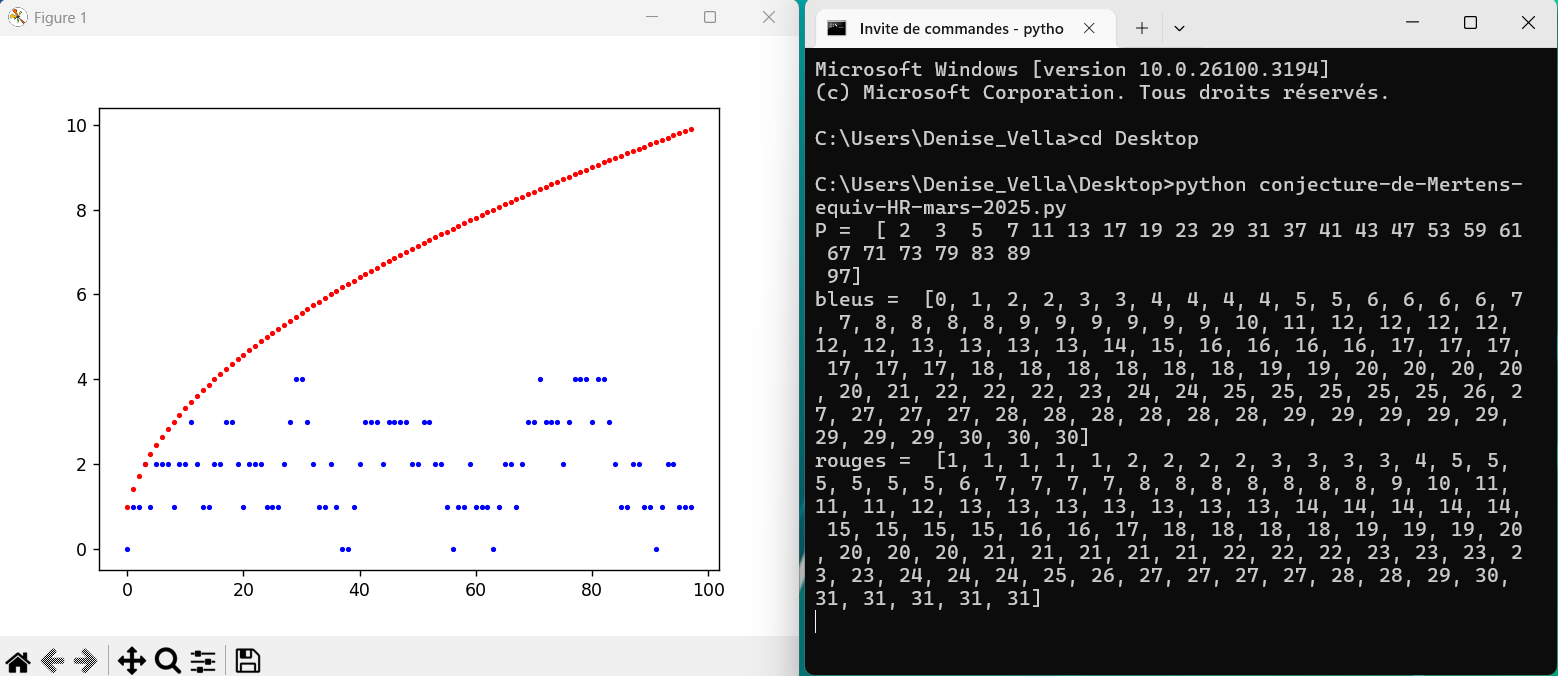 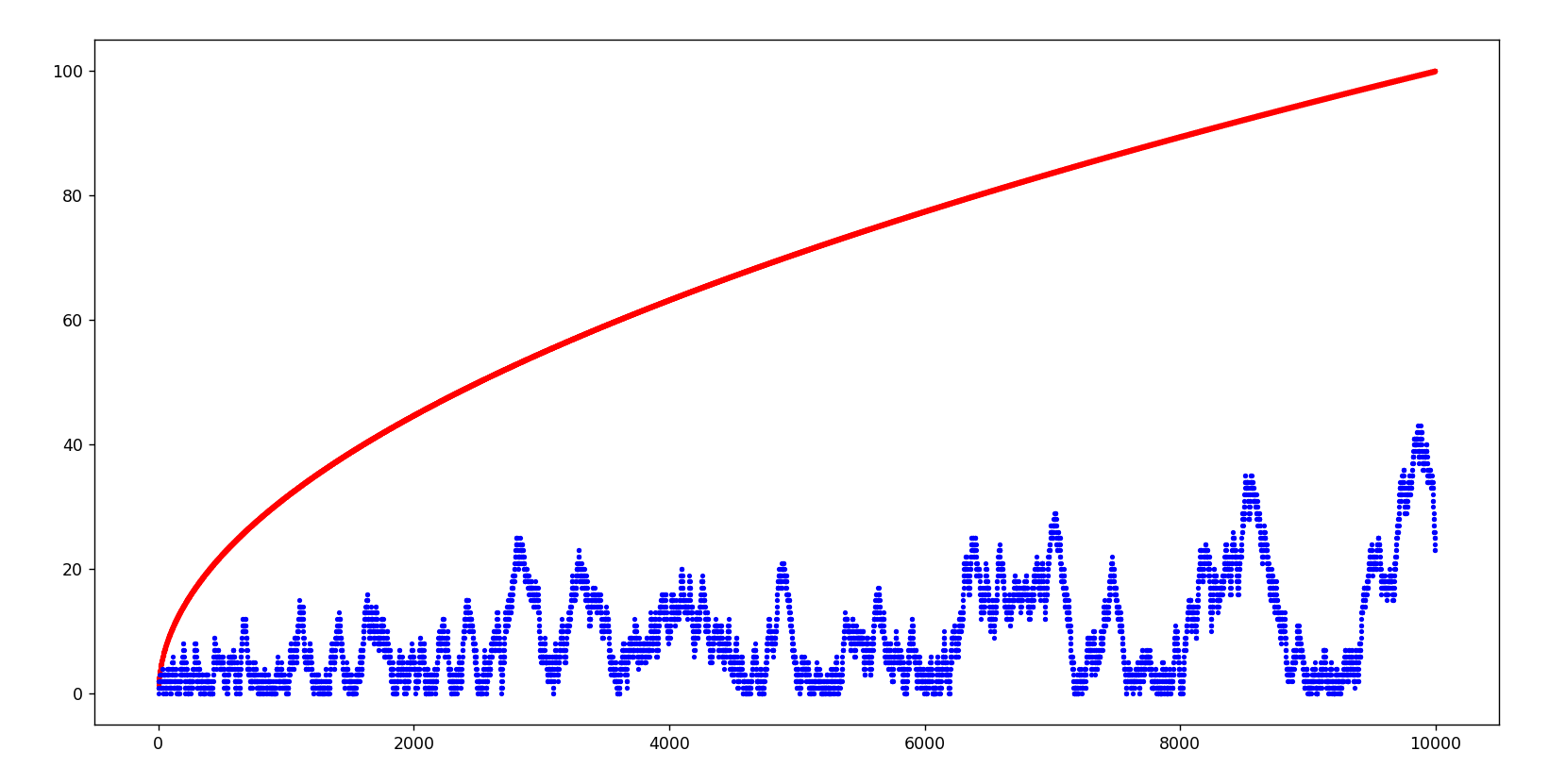 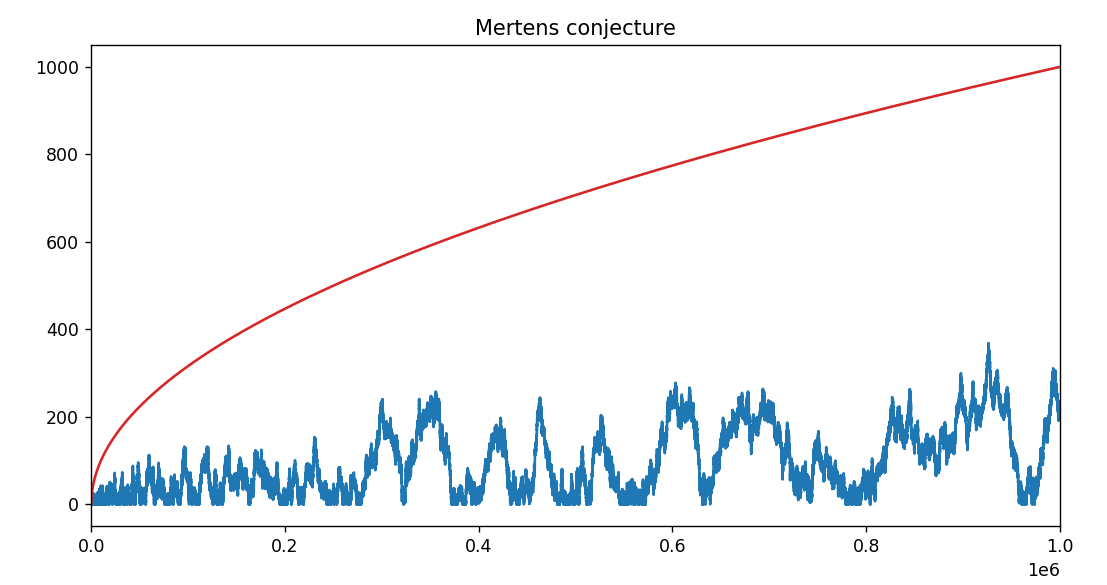 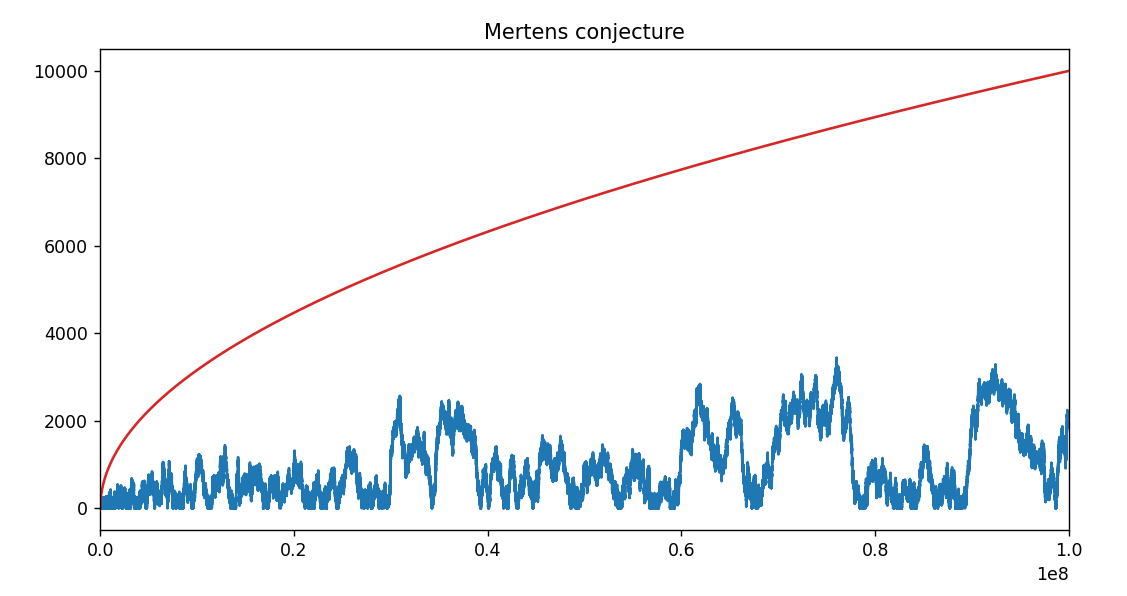
-
2.2.2025 : Depuis le temps qu’on me parlait du lit à deux places des topos, ça aurait dû me faire penser à la notion de bicouche en cristallographie (ici, c’est une bicouche de spins).
La bicouche de Goldbach est constituée de deux couches superposées de spins : sur la couche du bas (bleue), on voit ligne par ligne les divisibilités par 2, 3, 4, notées par des pixels bleus, parmi des pixels blancs. La couche du haut (rouge) est identique à la couche du bas. On imprime ces deux couches sur de bons vieux transparents pour rétroprojecteur (ou sur des calques TheGimp).
Pour trouver les décomposants de Goldbach de n (supérieurs à √ n), il faut faire glisser (= translation = décalage = shift) les transparents l’un par rapport à l’autre de n (le transparent des pixels bleus dit "p est premier" (si à son abscisse est positionnée une colonne de pixels blancs, dans le premier quadrant, strictement entre la ligne de 1 et la diagonale x=y), le transparent des pixels rouges dit "le complémentaire n-p de p est premier".     
C’est vraiment ce à quoi avait pensé Charles-Ange Laisant avec ses tirettes  , mais ici, on détaille toutes les divisibilités. , mais ici, on détaille toutes les divisibilités.
-
janvier 2025 : maximiser un produit de sinus, ou un produit de restes, sans test de primalité (ou revenir à l’ancien temps)

-
février 2025 : Harmoniques (décomposants de Goldbach de n=40)
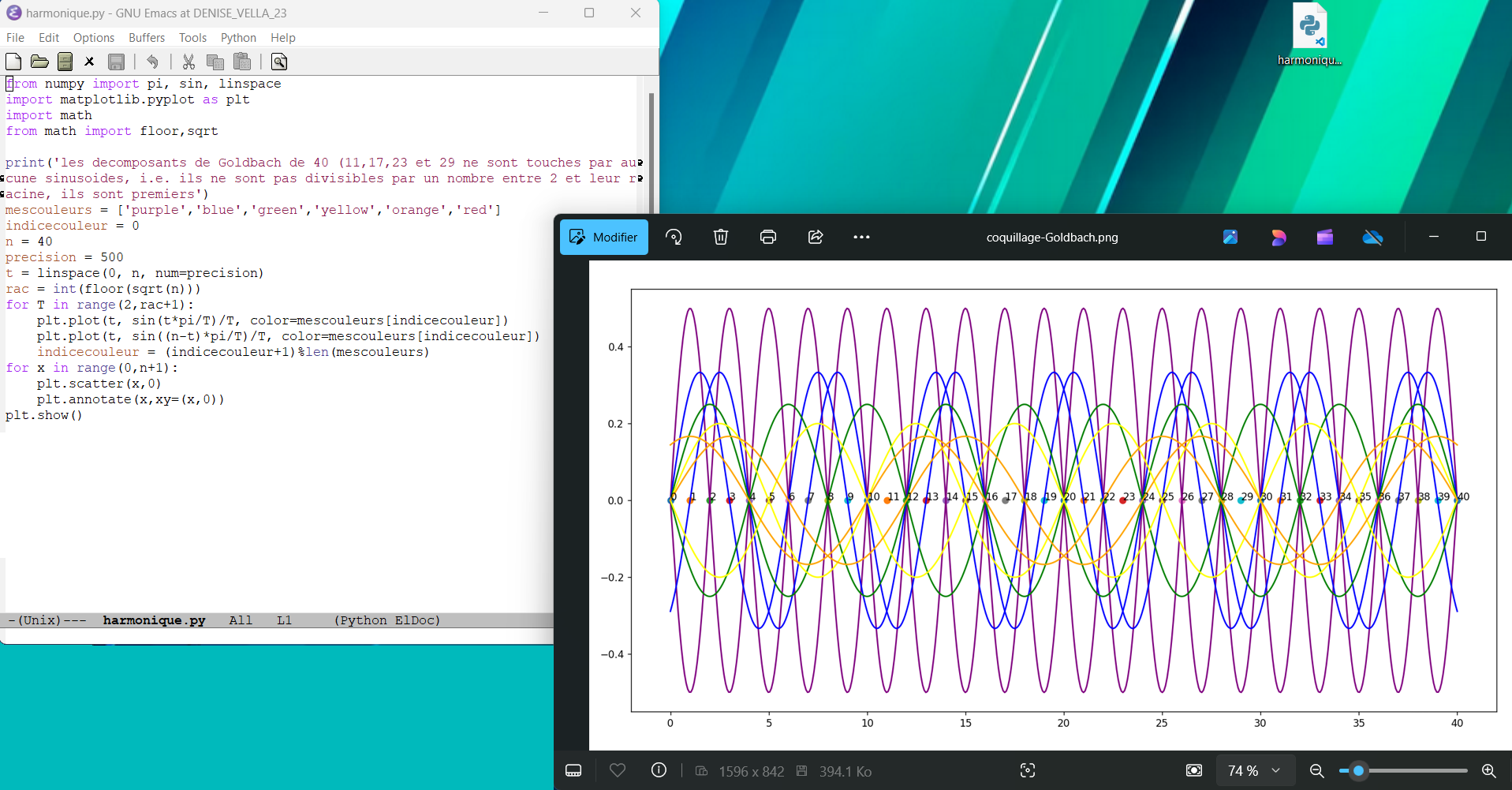
-
octobre 2024 : de l’importance des bijections (779)
 reprise reprise 
-
♥ 8.11.2024 : qui utilise des automorphismes intérieurs sans en avoir conscience
 petit memo pour division euclidienne petit memo pour division euclidienne 
-
traduction en français d’une conférence d’Alain Connes (100 ans des Acta Mathematica)

-
2025 : certains articles fondateurs de la mécanique quantique ont 100 ans ; l’article de Paul Dirac de 1925 Les équations fondamentales de la mécanique quantique
 l’article de Born-Jordan Sur la mécanique quantique l’article de Born-Jordan Sur la mécanique quantique  traduction du début de l’article de Born-Heisenberg-Jordan traduction du début de l’article de Born-Heisenberg-Jordan 
-
traduction d’un article d’Euler au sujet de la fonction de Lambert

-
oubli de poster en janvier 2023
 
-
30.12.2024 : illustration de la façon dont fonctionne la formule exacte de Riemann ((62), en bas de la page 296), trouvée dans la traduction par Barkan et Sklar du texte de Siegel "On Riemann’s Nachlass for Analytic Number Theory" de 1932
  formule intégrale sur le carré unité pour ζ trouvée dans une vidéo ici
formule intégrale sur le carré unité pour ζ trouvée dans une vidéo ici 
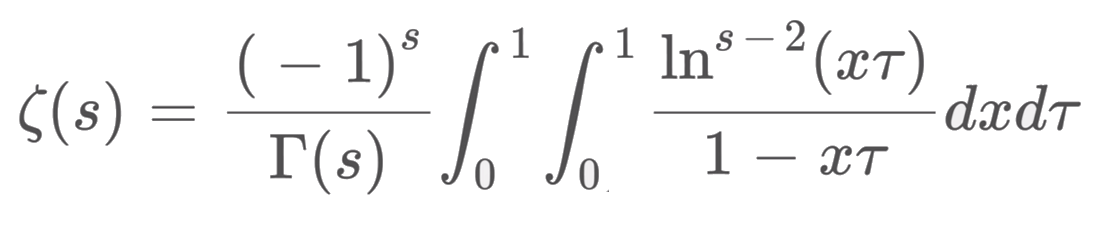
-
décembre 2024 : Sophie Germain et la moyenne des courbures

-
31.12.2024 : Fonction des zéros vers des réels dont les parties entières sont quasi-successives

-
31.12.2024 : Produit eulérien pour enfants

-
décembre 2024 : Traduction de l’artice Sur une idée de Michael Atiyah, dans lequel il est question de la fonction de Lambert

-
décembre 2024 : rotations complexes pour premiers, matrices 2x2

-
♥♥ décembre 2024 : zéros de zeta, fonction W de Lambert
 Tentative de simplification Tentative de simplification  Référence au sujet de la fonction de Lambert Référence au sujet de la fonction de Lambert  
-
18.12.2024 : deux spirales sur une spirale

et il suffit d’inverser un signe pour aller vers l’œil du cyclone 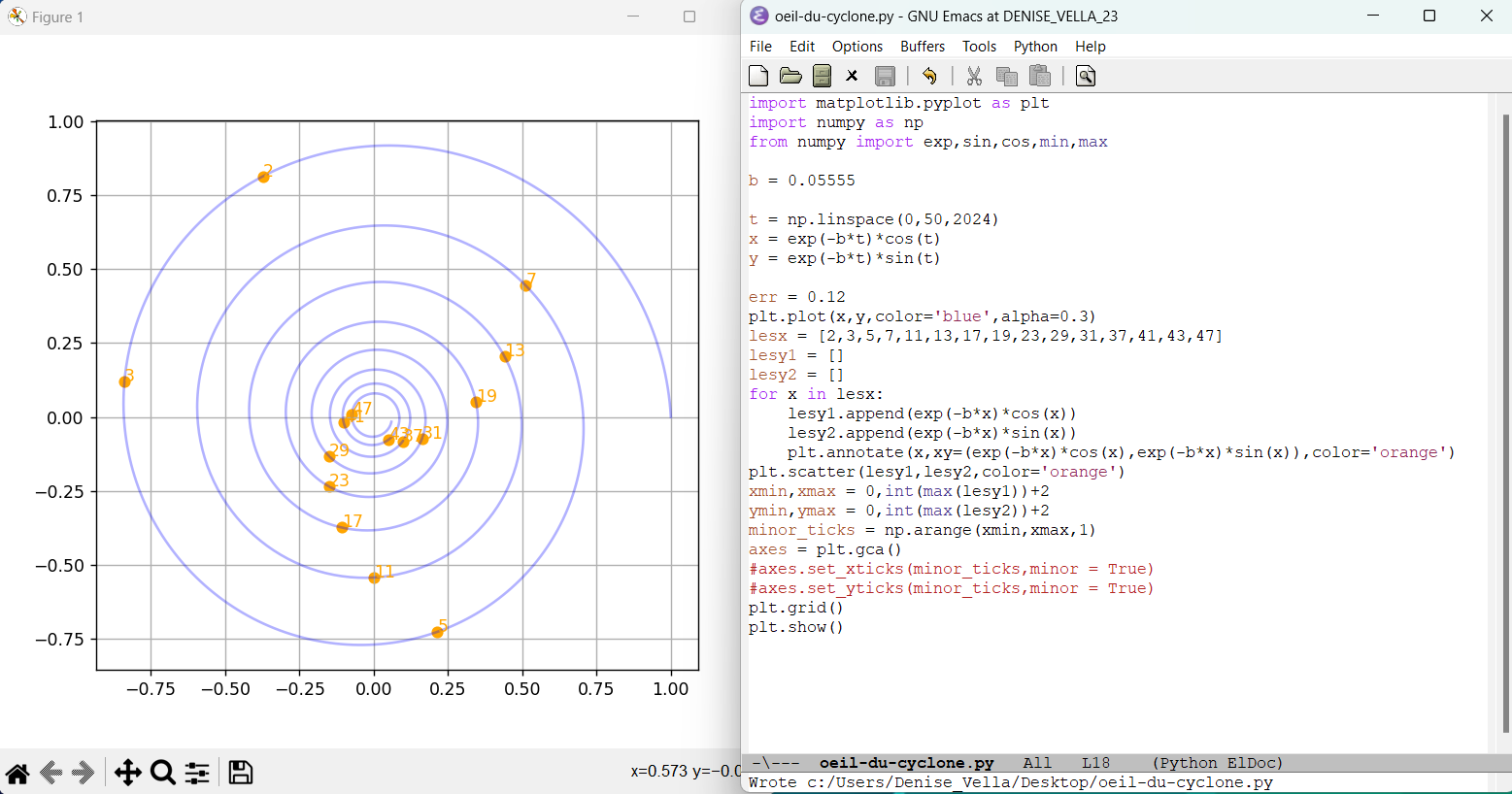
-
17.12.2024 : Plot des valeurs propres qui entraînent soit une opposition de phase soit une phase des fonctions f(x) = 4 π sin(4 π x)/x et g(x)=4 π sin(4 π x+(m/2)+π)/x
   65 n’est pas une valeur propre 65 n’est pas une valeur propre 
-
15.12.2024 : presque programmer l’opérateur prolate

-
8.12.2024 : échelle log-log
 
 
 
 
 
 
et nombre d’or
   
-
5.12.2024 : somme des inverses des logarithmes des entiers de 2 à x, jusqu’à 999999999

-
7.12.2024 : formulaire résumé concernant les résultats autour des nombres premiers

-
5.12.2024 : aujourd’hui, j’ai repris le programme de fonctions sphéroïdales prolate pour calculer les zéros de ζ , j’ai réussi à en calculer seulement 4 : dès que je change de coefficient, le programme les perd (utilisation des formules du Milton Abramowitz et Irene Stegun)
  
précédemment, j’avais ça 
-
4.12.2024 : calculs pour comparer abs(π(x)-Li x) et √x.ln x du fait d’une remarque dans l’article du Clay Institute de Bombieri traitant de l’Hypothèse de Riemann
 haut de la page 4 ici haut de la page 4 ici  
-
27.11.2024 : programmation autour de formules d’André LeClair, Guilherme França et Giuseppe Mussardo
 calculs pour comparer abs(π(x)-Li(x)) et √(x).ln(x) calculs pour comparer abs(π(x)-Li(x)) et √(x).ln(x) 
-
♥ 24.11.2024 : résumé des résultats dans le plan complexe (nombres-bases pour calc. rac. niemes)
 Bon tempo, ou bon, tant pis ! Bon tempo, ou bon, tant pis ! 
-
22.11.2024 : nombres bases et valse réciproque des parties imaginaires des zéros non triviaux par fonction de Lambert
 régression logarithmique pour quelques zéros de ζ régression logarithmique pour quelques zéros de ζ  redécouvrir la poudre : exposants de partie réelle ½ et inversion redécouvrir la poudre : exposants de partie réelle ½ et inversion 
-
20.11.2024 : la moitié de tout : une formule qui trouve "presque" les parties imaginaires des zéros non triviaux de ζ

-
♥♥ 9.11.2024 : démonstration d’une découverte qu’on avait faite en février 2024, au sujet de la somme des inverses des racines carrées des nombres entiers positifs (voir étonnement constant 22.2.2024)

Après tout, l’idée initiale d’Euler...  petit programme pour se faire une idée avec séries finies et exposants rationnels simples petit programme pour se faire une idée avec séries finies et exposants rationnels simples   
-
octobre 2024 : memo

-
octobre 2024 : s’initier à la théorie de Galois (en ayant des petites galères de signes) (778)

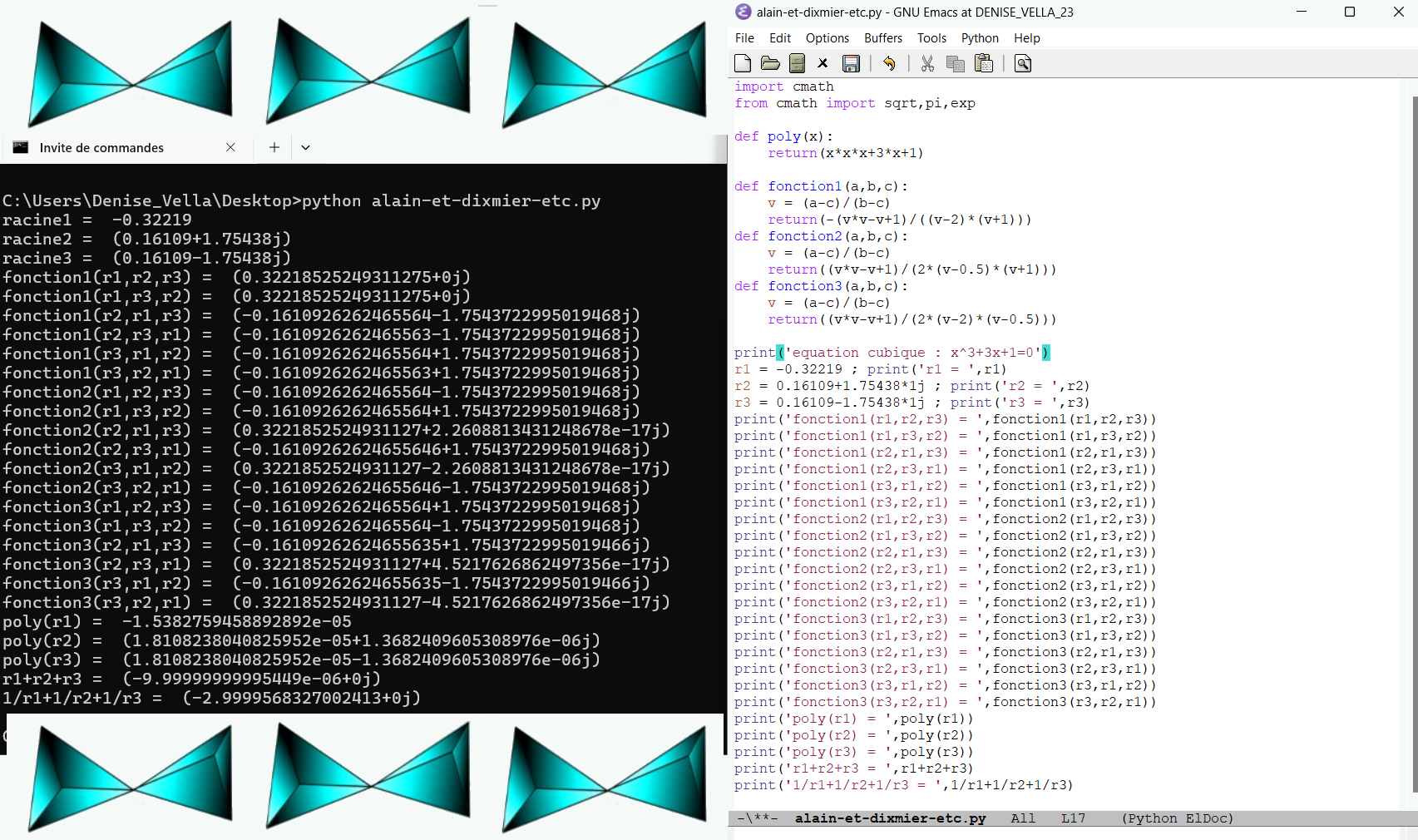
référence : Sur les équations du 3ème et du 4ème degré : de Galois et Lagrange au miracle de Morley, un article d’Alain Connes et Jacques Dixmier dans la Revue l’Enseignement des mathématiques   incompréhension concernant les racines (conférence février 2024)
incompréhension concernant les racines (conférence février 2024)  11.11.2024 : les zéros vont par 4 11.11.2024 : les zéros vont par 4 
-
octobre 2024 : briser les symétries (777)
 nombres 90 à 102 nombres 90 à 102 
-
9.10.2024 : transcription / traduction de la thèse de Carl Friedrich Gauss
 version latine de la thèse extraite des Werke (la planche de dessins ne correspond pas à celle trouvée dans la version anglaise sur la toile) version latine de la thèse extraite des Werke (la planche de dessins ne correspond pas à celle trouvée dans la version anglaise sur la toile)  un texte explicatif de J.-P. Friedelmeyer un texte explicatif de J.-P. Friedelmeyer  
-
♥ Octobre 2024 : opérateurs matriciels pour conjecture de Goldbach (776)
 revenir à la démonstration du théorème de Morley
revenir à la démonstration du théorème de Morley 
Transcription d’une conférence d’Alain Connes de 2004 au Cern  Traduction Google Traduction Google  tentative ratée de passer d’un triangle à un autre tentative ratée de passer d’un triangle à un autre 
-
29.9.2024 : ellipses d’Hypatie (775)
  les 2p les 2p  
lien vers le petit extrait du film Agora (2009)  (en) (en)   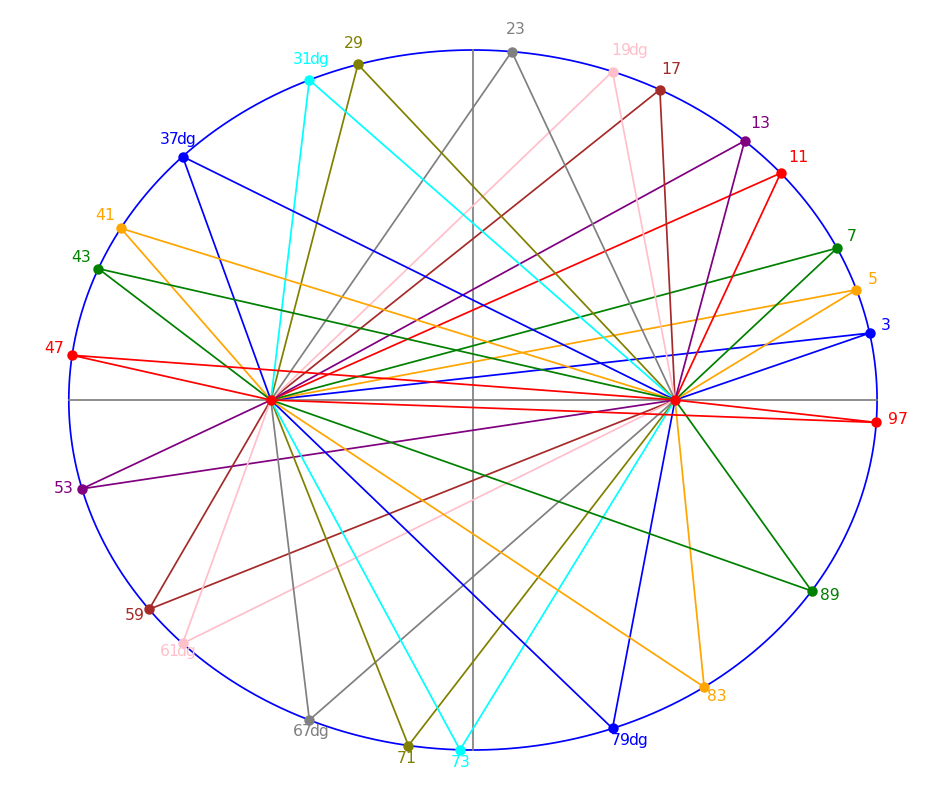 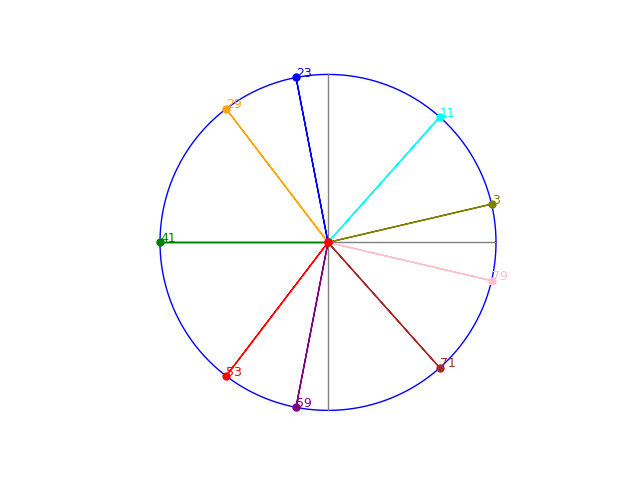 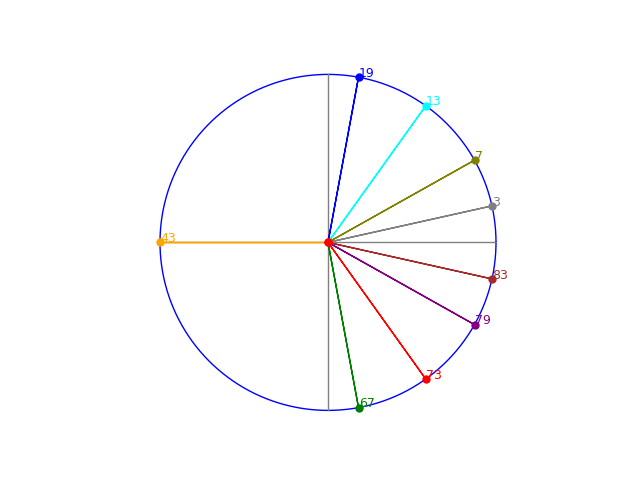
-
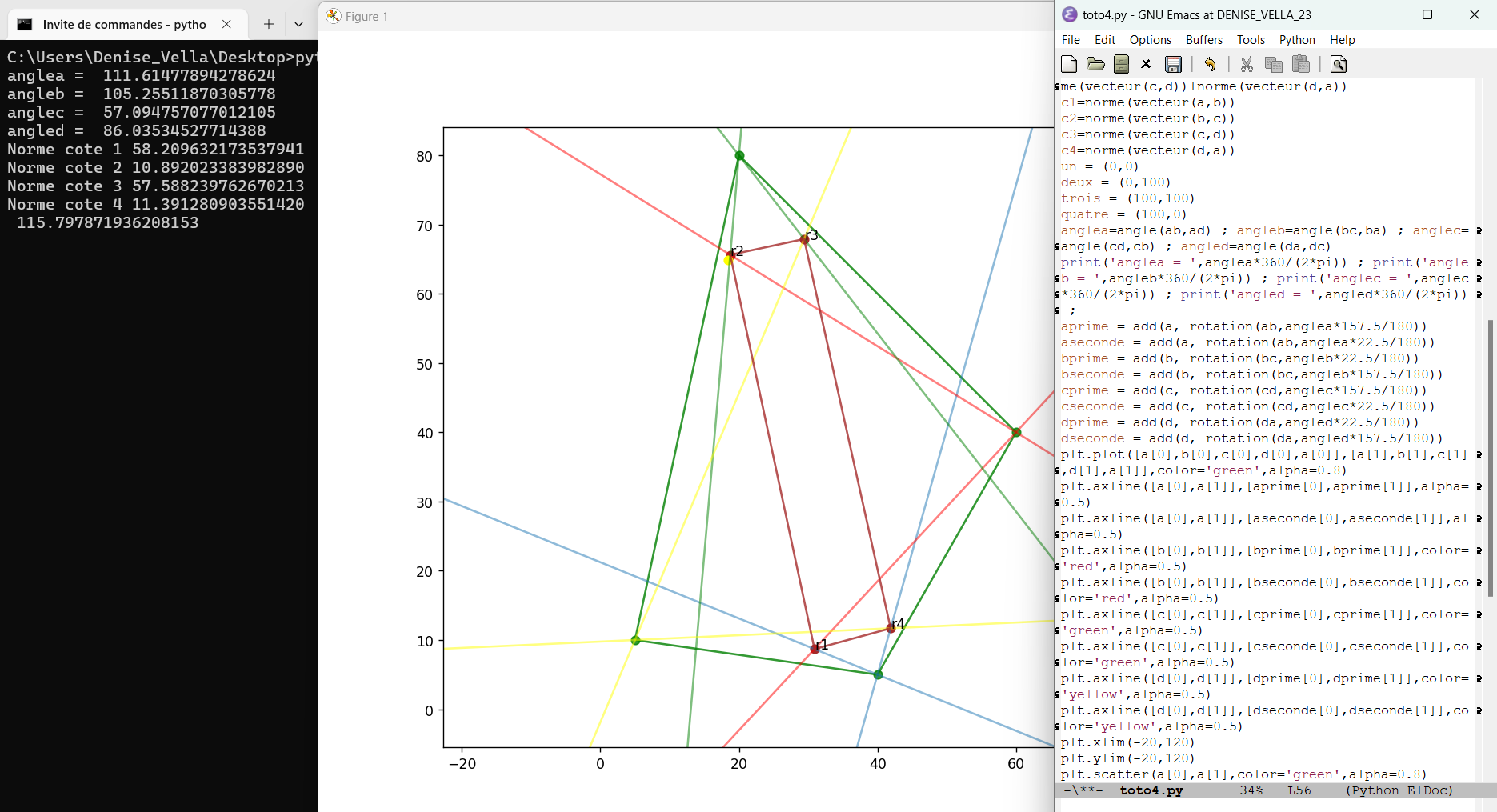
septembre 2024 : rectangle de Morley sans triangles (774) avril 2025 : j’ai mis un geogebra ici, pour comprendre (ou pas ;-) ce qui se passe
-
septembre 2024 : programmer la formule pour π(x) de l’article d’Alain Connes Around Wilson’s theorem (773)
  (attention : le nombre entier n=4, bien que non divisible par (n-1)!, est composé) (attention : le nombre entier n=4, bien que non divisible par (n-1)!, est composé)
-
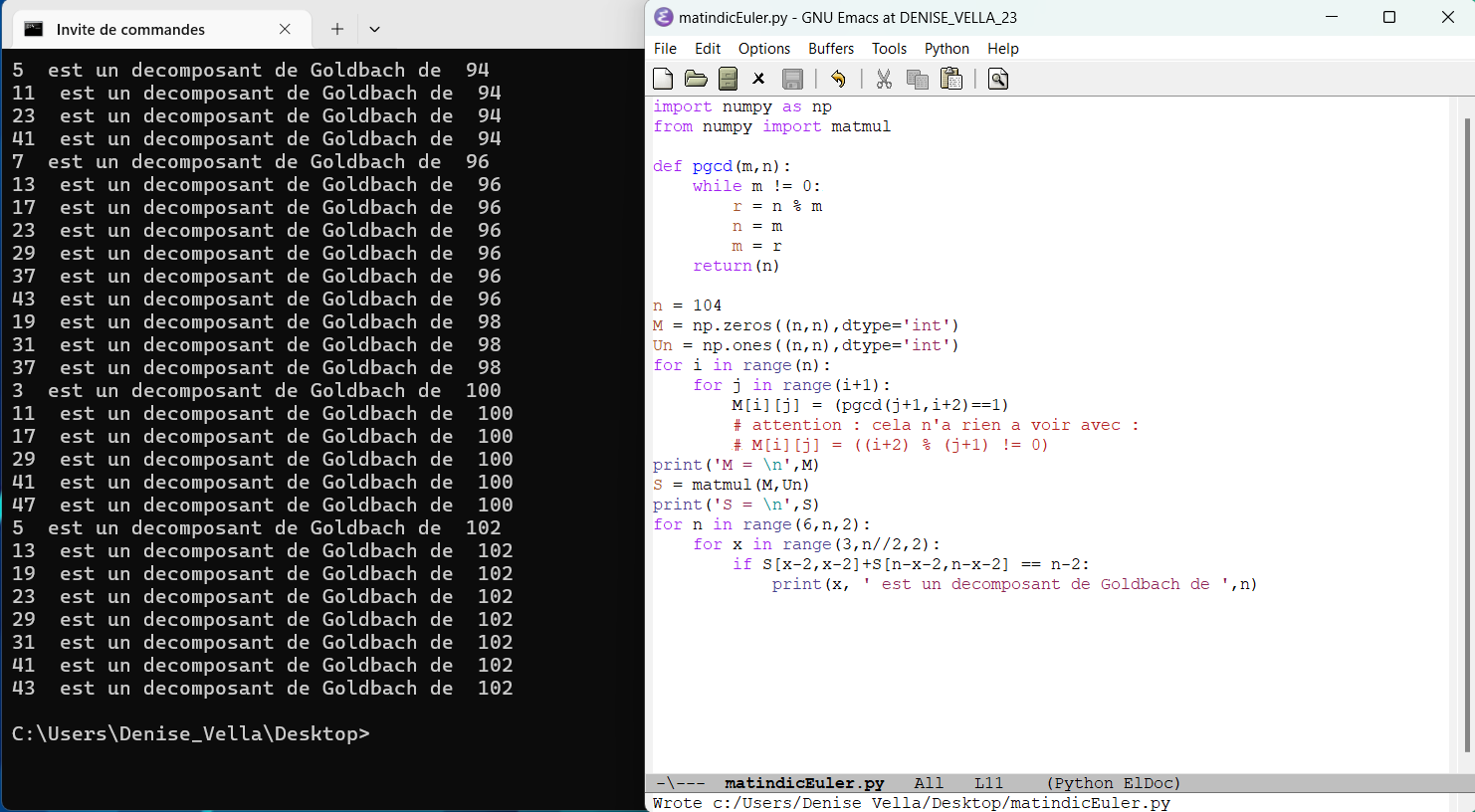
septembre 2024 : rappel de Goldbach et matrices (772)
-
août 2024 : le sympathique rectangle du quadrilatère, en utilisant 4 petits triangles de Morley (programme laborieux) (769)
 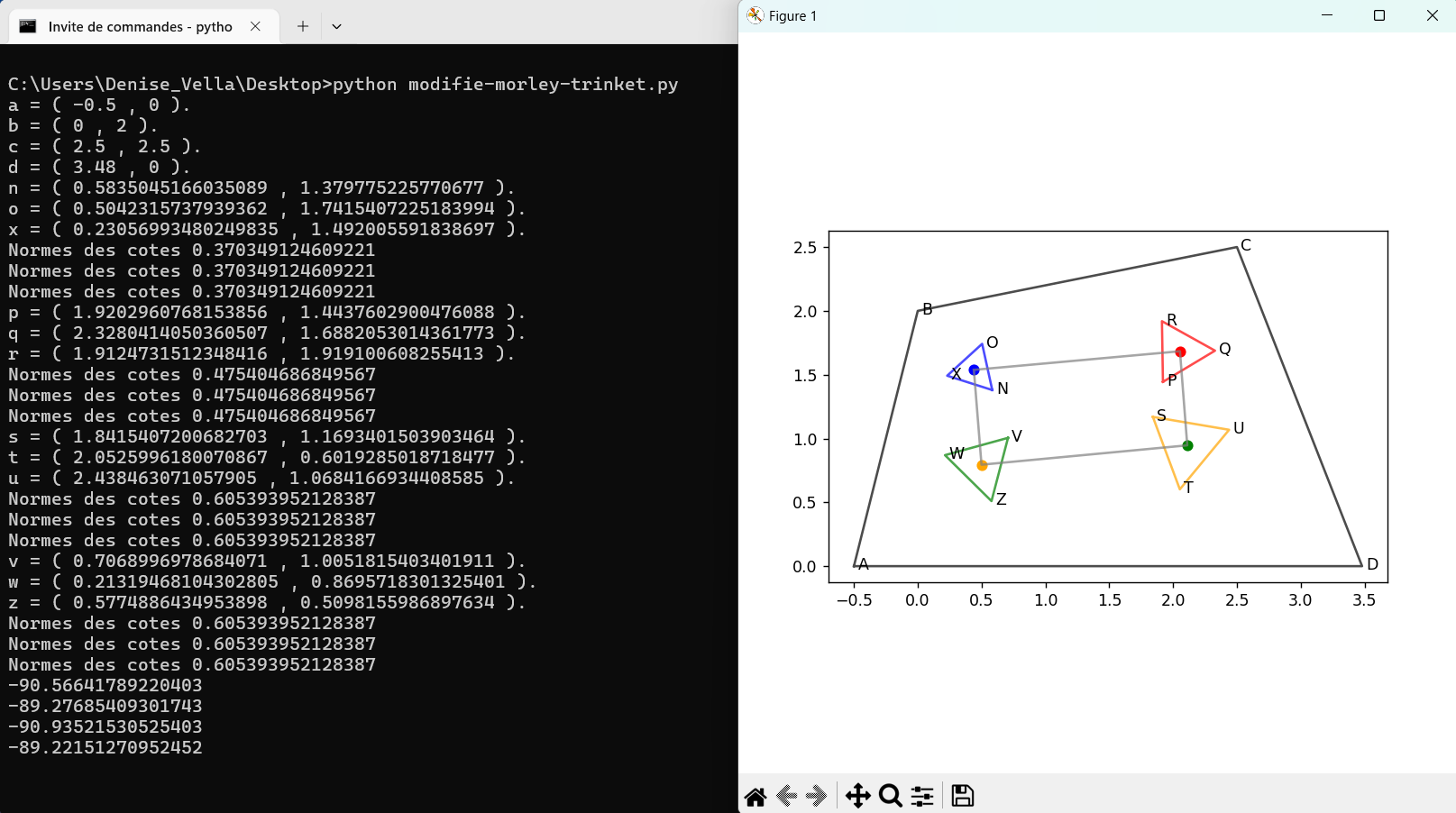 et tant pis, même si j’aurais bien aimé régulariser un quintilatère et tant pis, même si j’aurais bien aimé régulariser un quintilatère 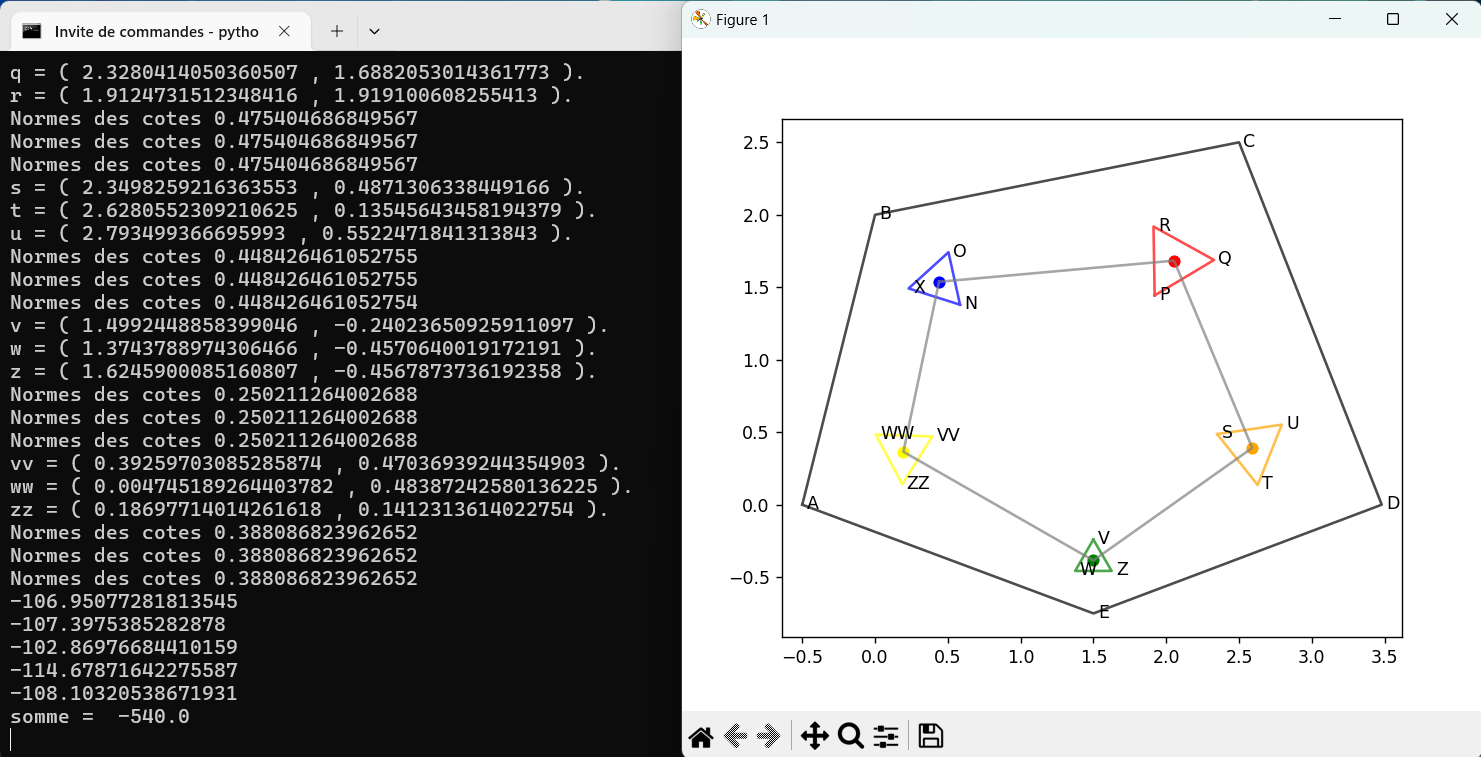
-
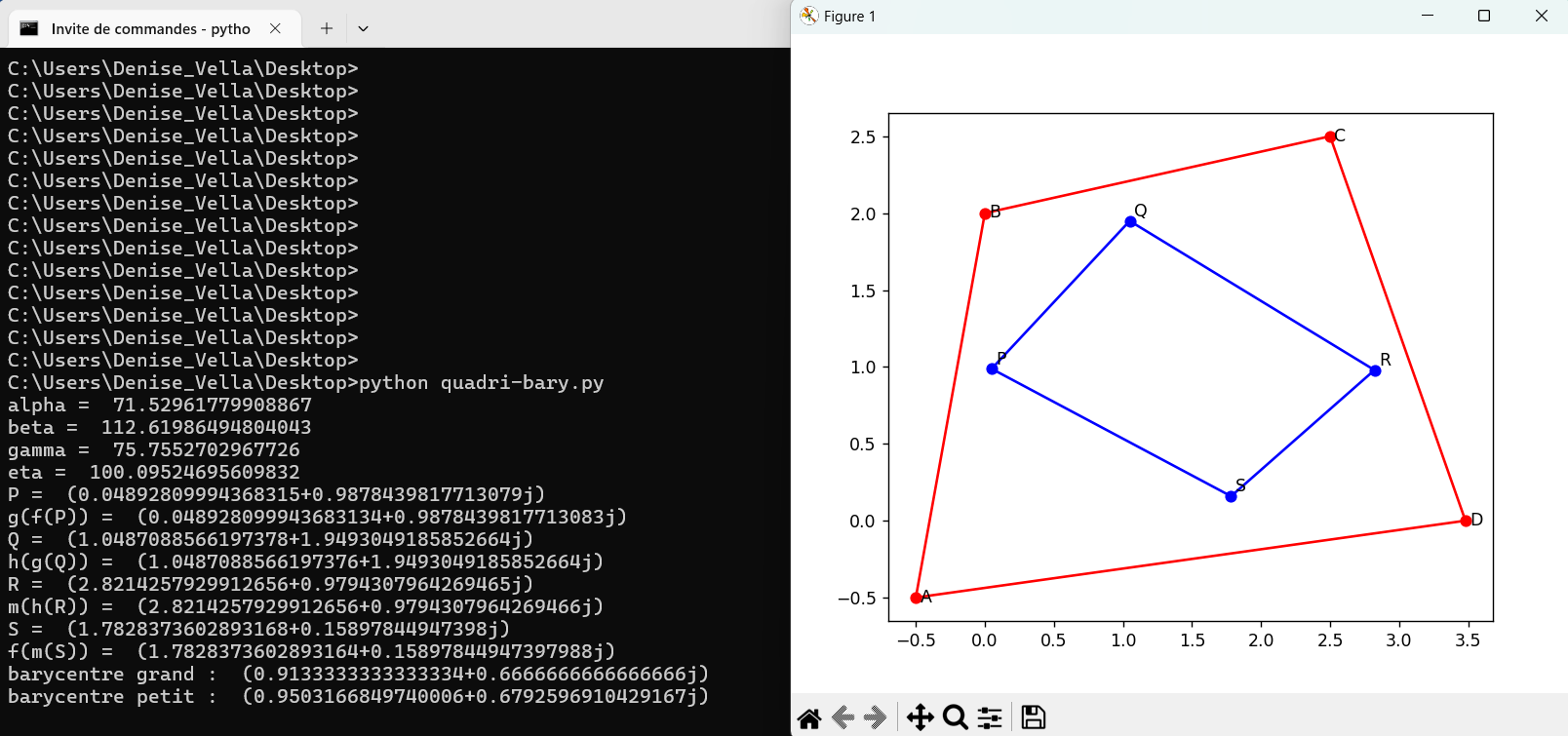
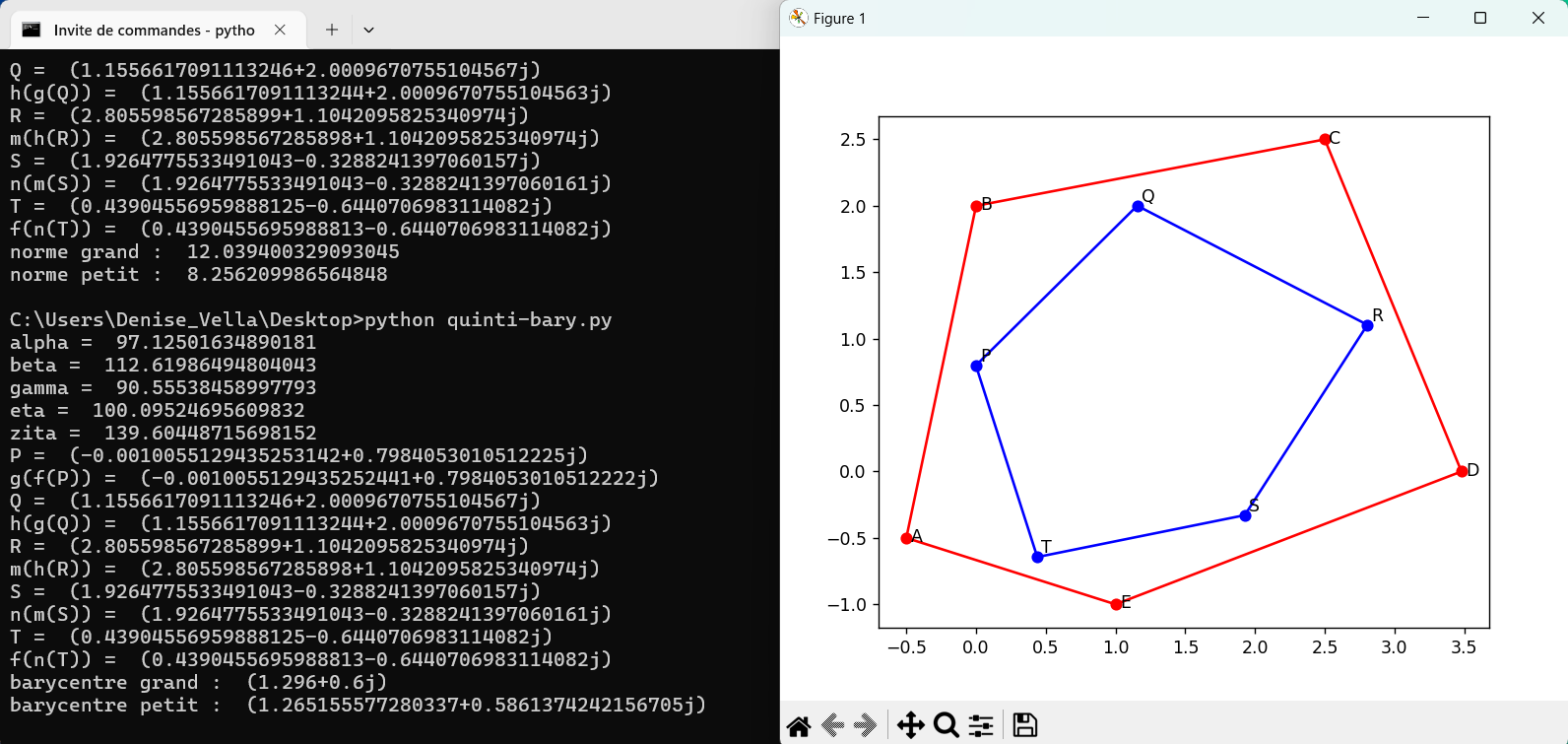
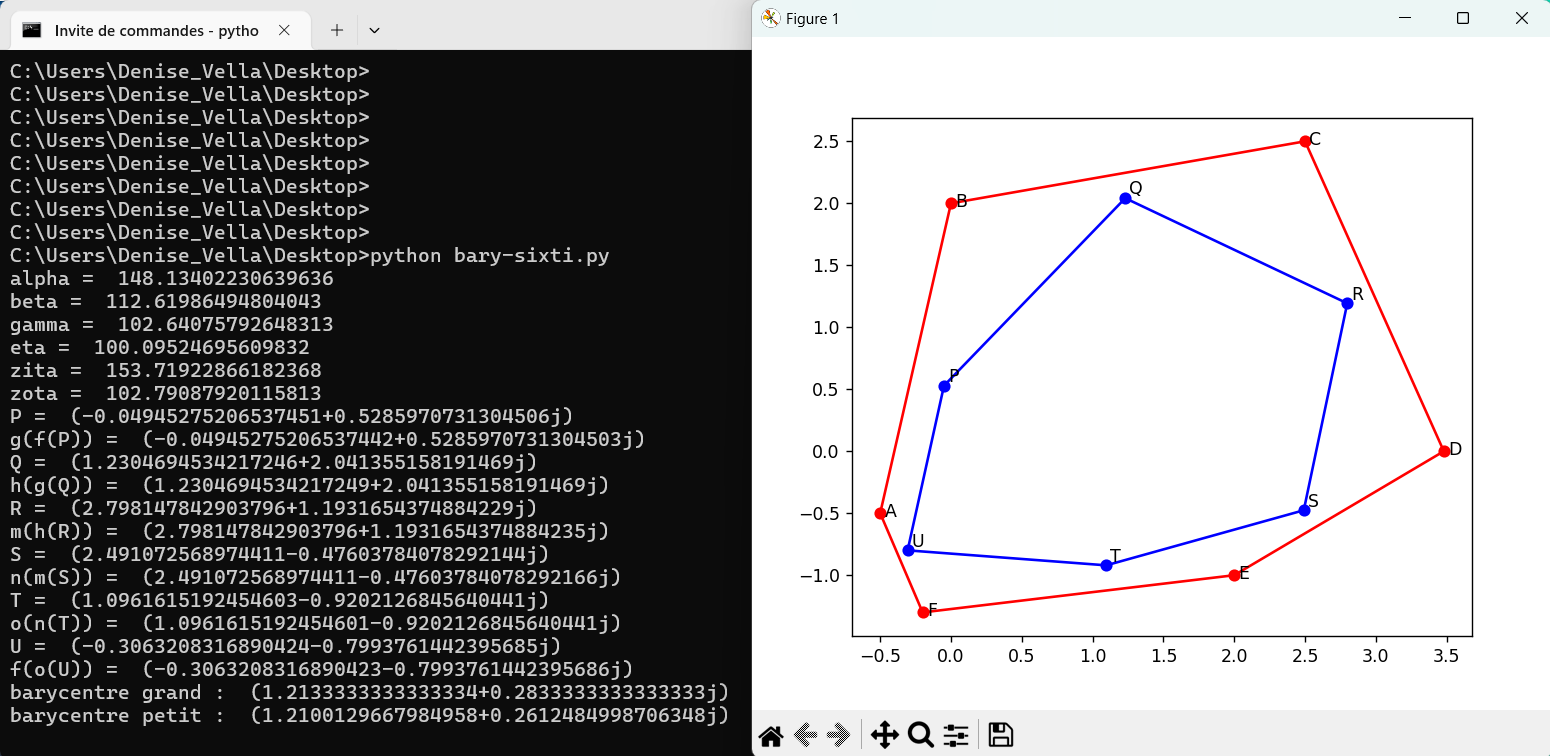
août 2024 : Morley pour quadrilatère, quintilatère (pentagone), sixtilatère (hexagone) avec points fixes corrects et calculs des barycentres de la figure et de sa transformée (768)
-
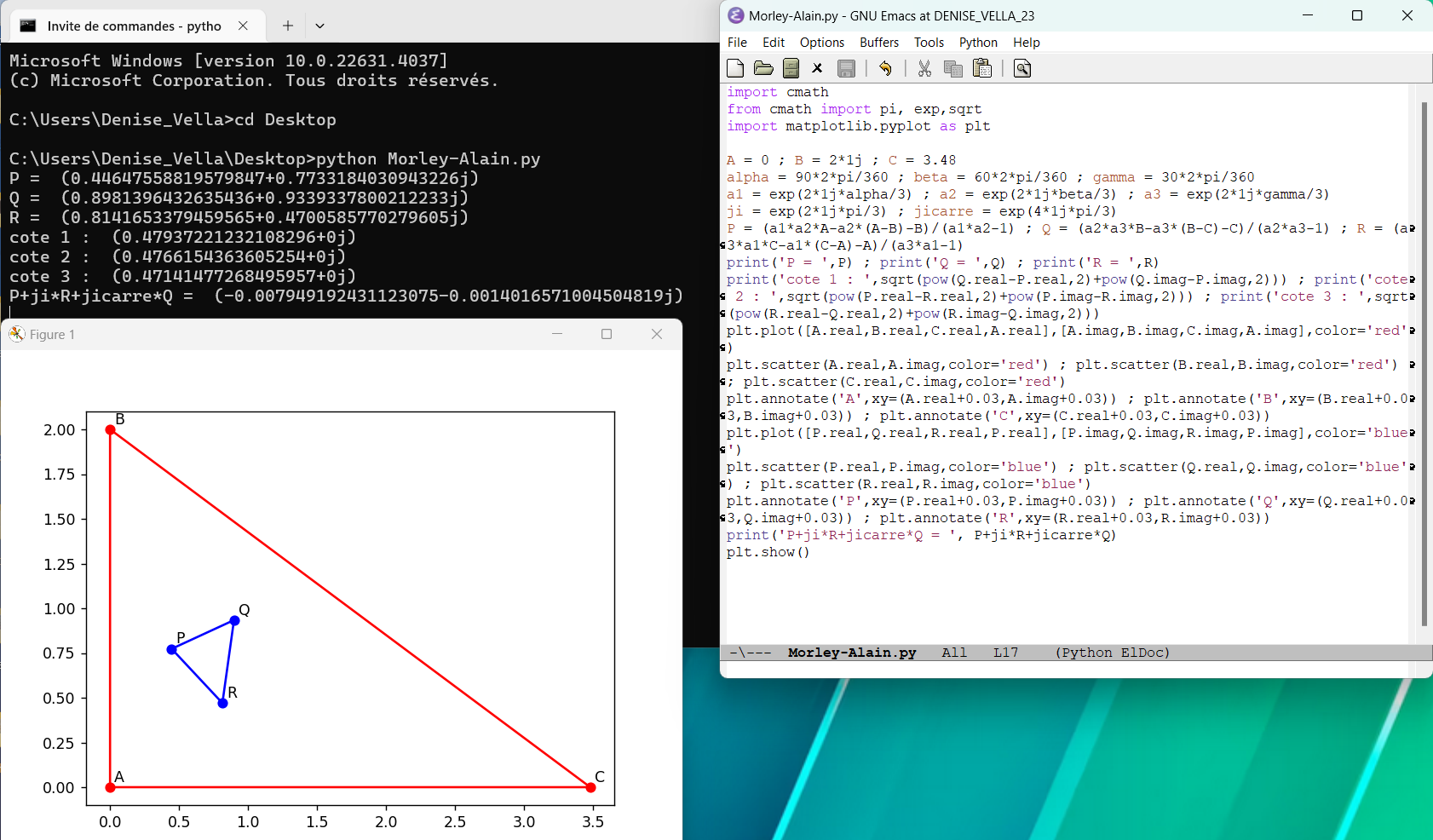
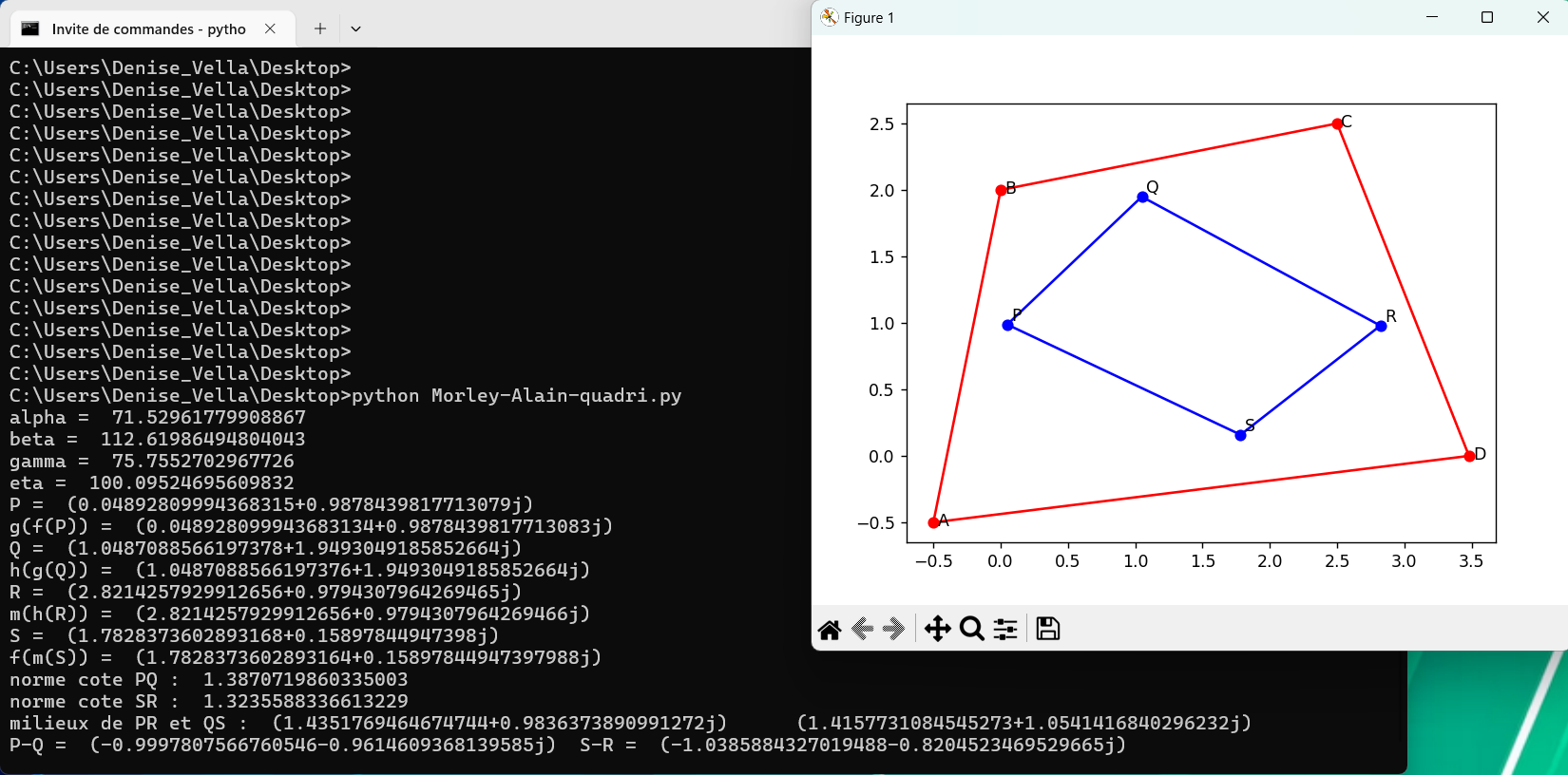
août 2024 : dessins en python pour triangle (preuve d’Alain Connes du théorème de Morley, points fixes, transformations affines) (767)
  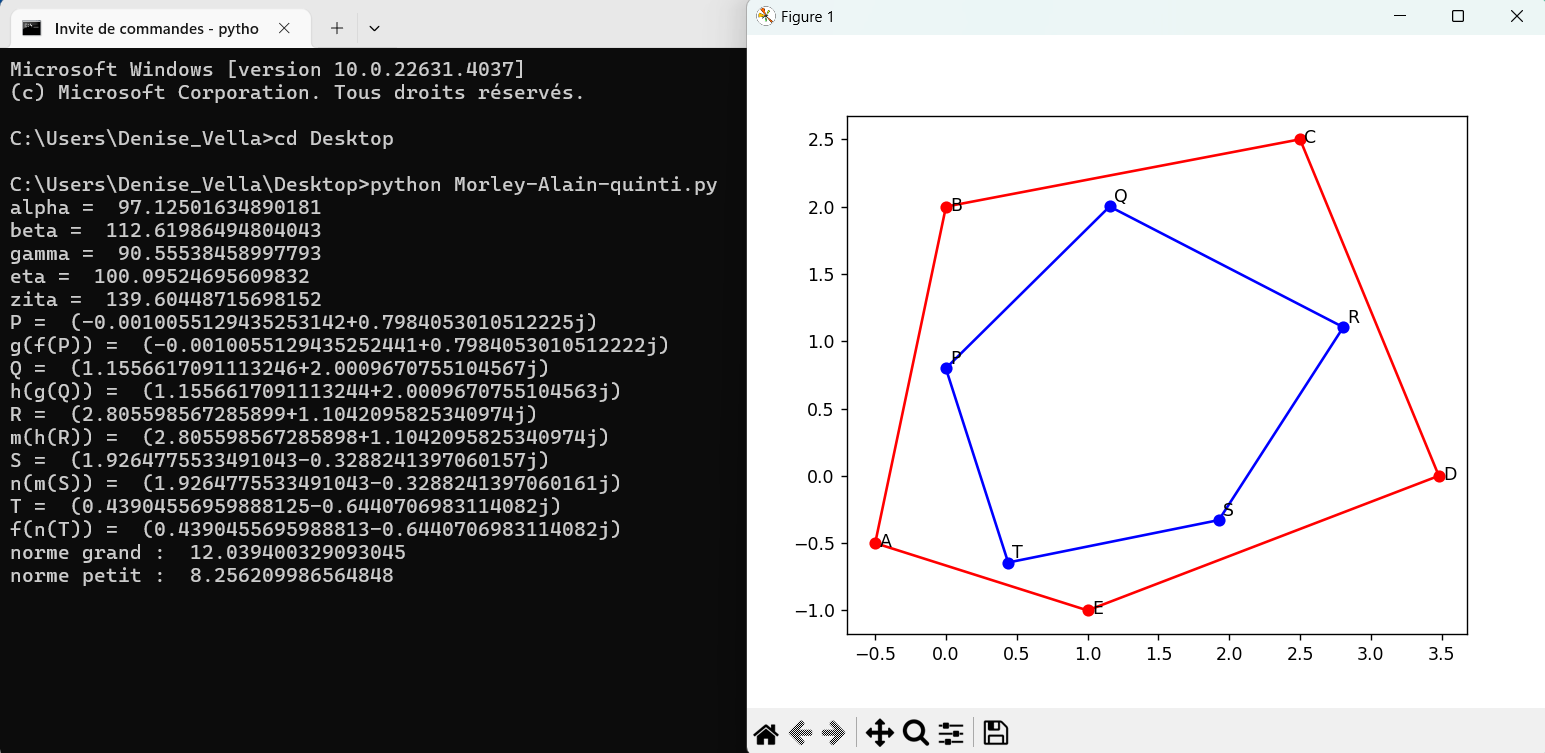
-
août 2024 : dessins en python de la preuve du théorème de Morley par Lubin (766)
 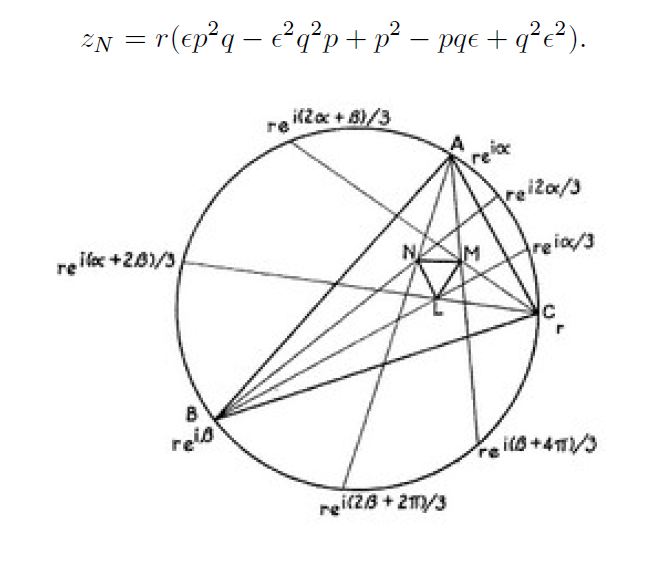 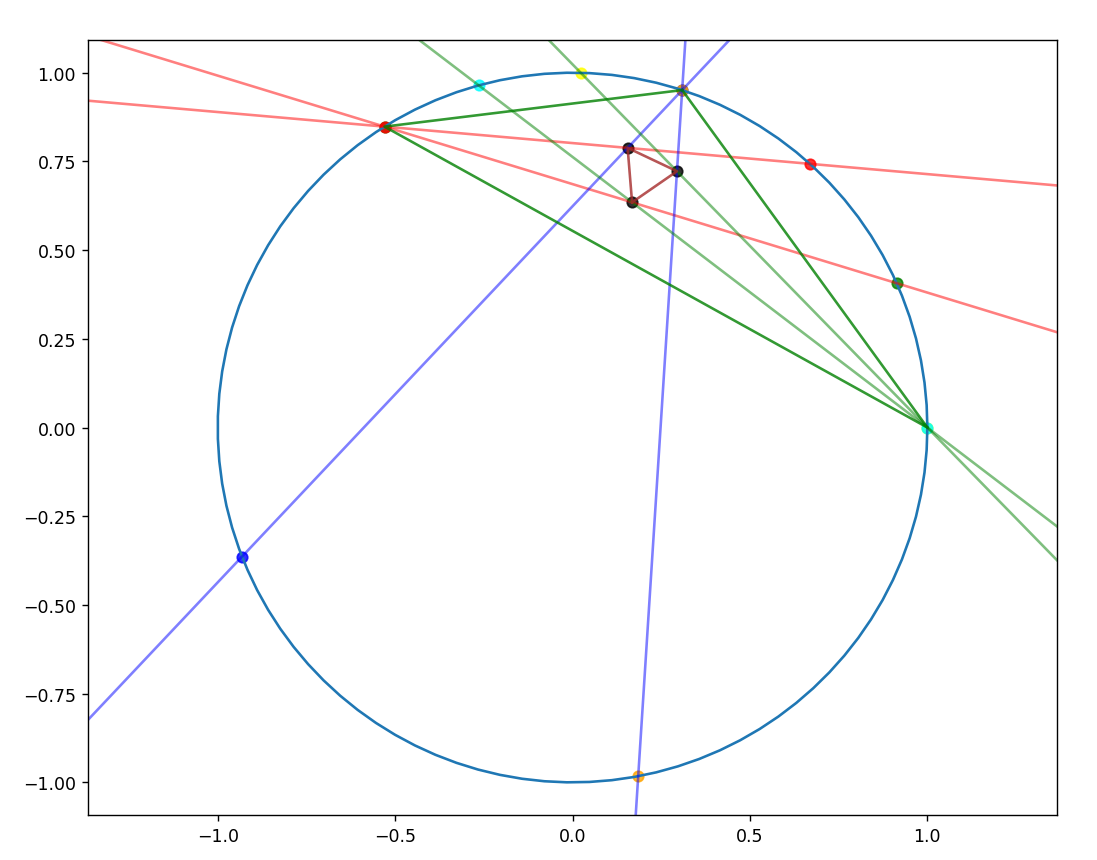 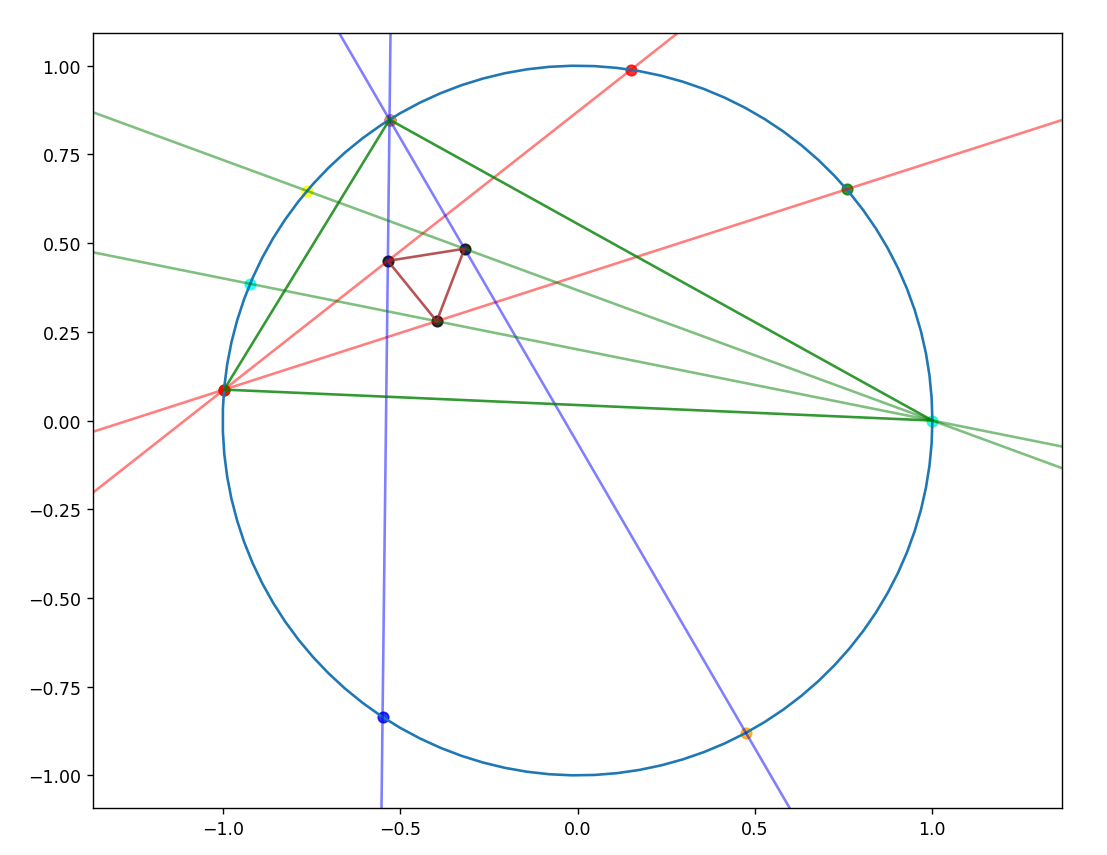
-
4.8.2024 : perseverare... (765)
  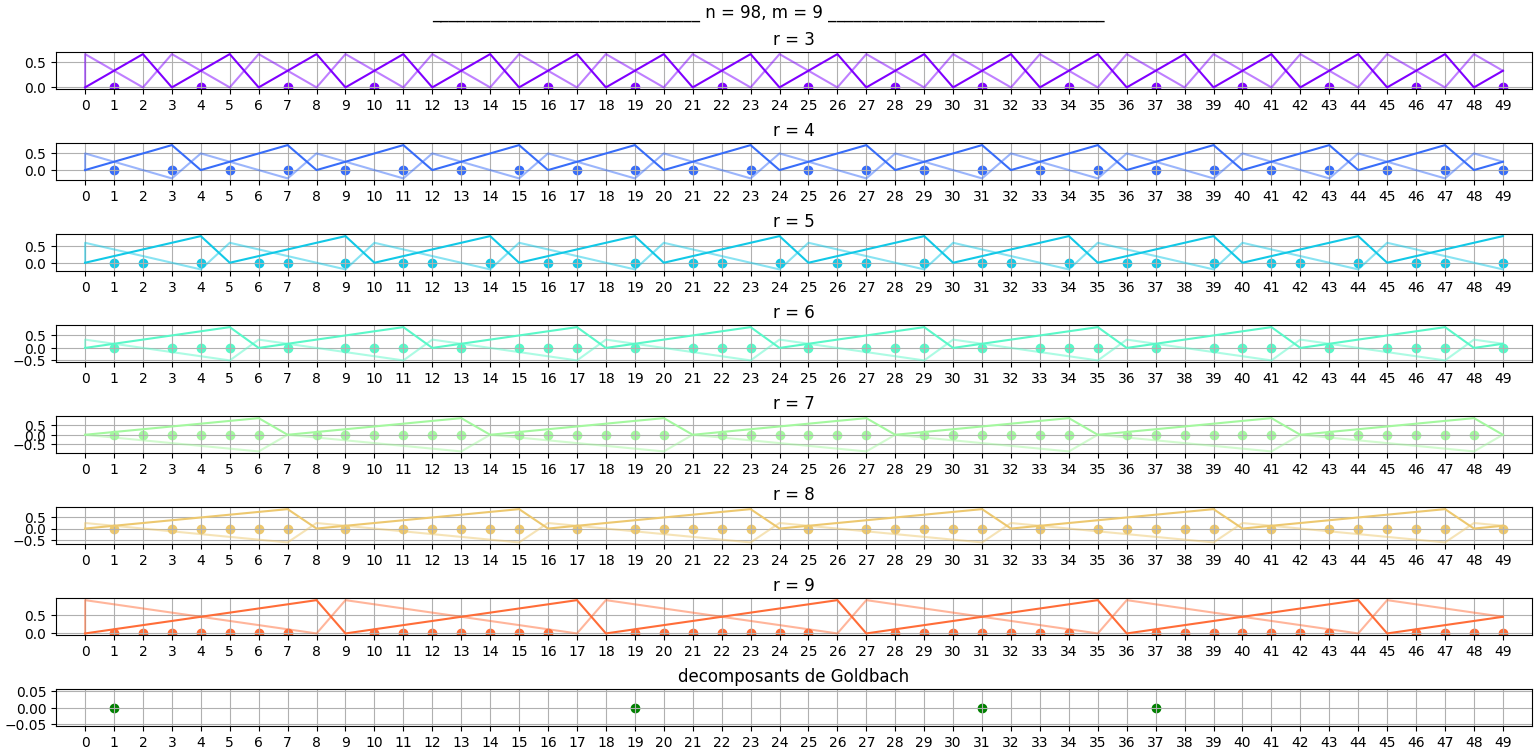 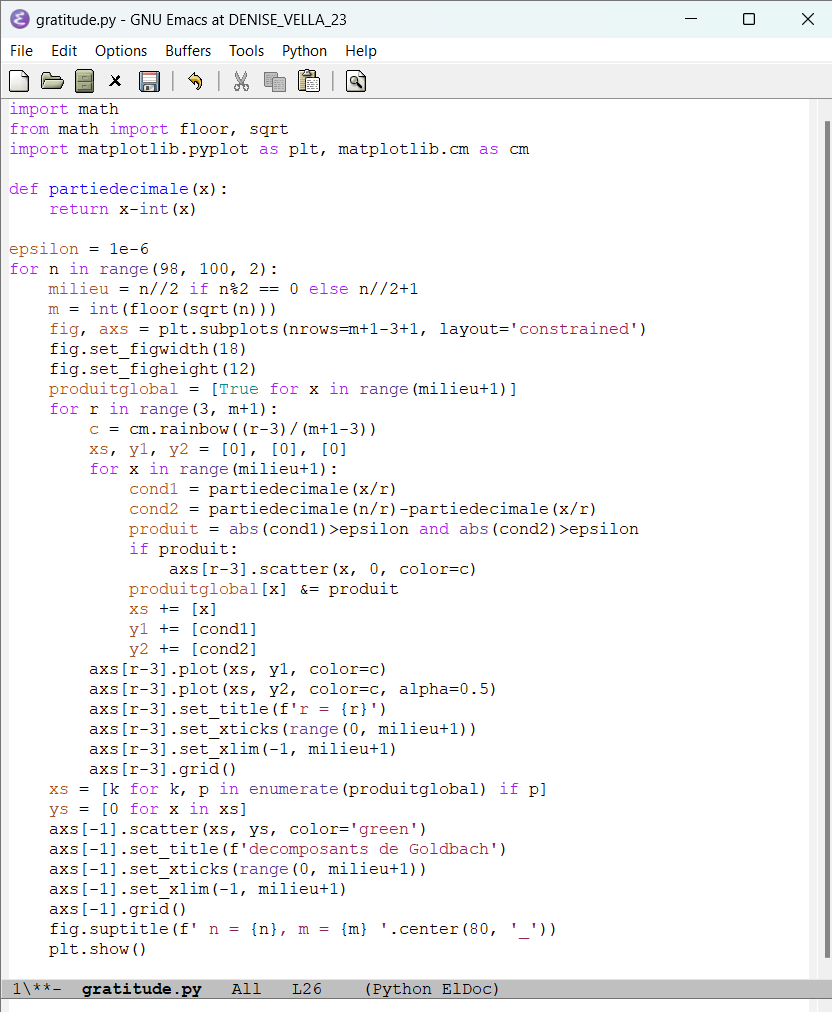
-
22.7.2024 : Sacs de... plage (et si on recousait les extrémités en 0 et n de chaque brin pour les refermer) (764)
 Toutes les courbes, deux par deux (pair-impair) qui se suivent de même couleur, l’une foncée, l’autre claire. Toutes les courbes, deux par deux (pair-impair) qui se suivent de même couleur, l’une foncée, l’autre claire.  tresses (seuls premiers, discretisation 1) tresses (seuls premiers, discretisation 1)  applet geogebra avec courbes translatables (k est le pair à décomposer, il faut mettre ses restes modulo 3, 5 et 7 dans les curseurs mais bouger les curseurs permet toujours de trouver un impair avec toutes ses images sur les différentes courbes qui sont non nulles) applet geogebra avec courbes translatables (k est le pair à décomposer, il faut mettre ses restes modulo 3, 5 et 7 dans les curseurs mais bouger les curseurs permet toujours de trouver un impair avec toutes ses images sur les différentes courbes qui sont non nulles)  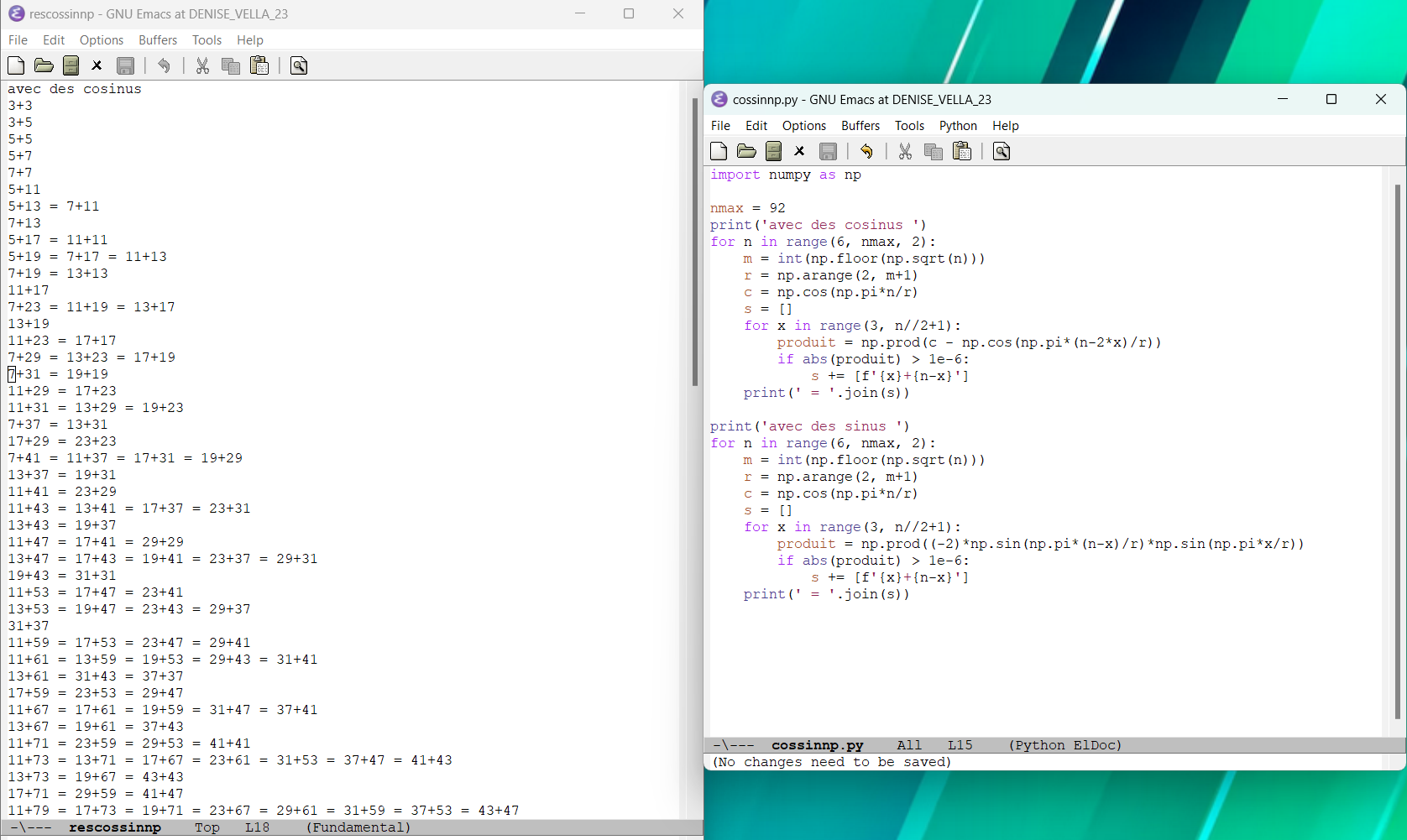 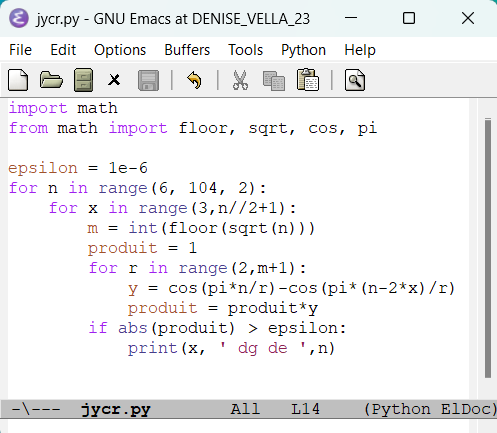
-
18.7.2024 : Chercher la raison (763)

-
12.7.2024 : valeurs contraintes et retour vers l’arithmétique (762)

-
10.7.2024 : décomposants de Goldbach et fonctions paires (761)
 fonctions paires fonctions paires 
-
8.7.2024 : décomposants de Goldbach dans le plan complexe (760)
 les courbes les courbes  papillons papillons  de 6 à 102 de 6 à 102 
-
1.5.2024 : le jour où les demi-droites s’alignèrent ou se perpendicularisèrent et dessins complexes (759)
-
Transcription en Latex de la Pierre de Rosette
 version html (contenant des images) : version html (contenant des images) : 
Table de correspondance de caractères (il faut exploiter les standards au maximum, comme dans le jazz)  
-
Physiciens et π converge très vite (758)
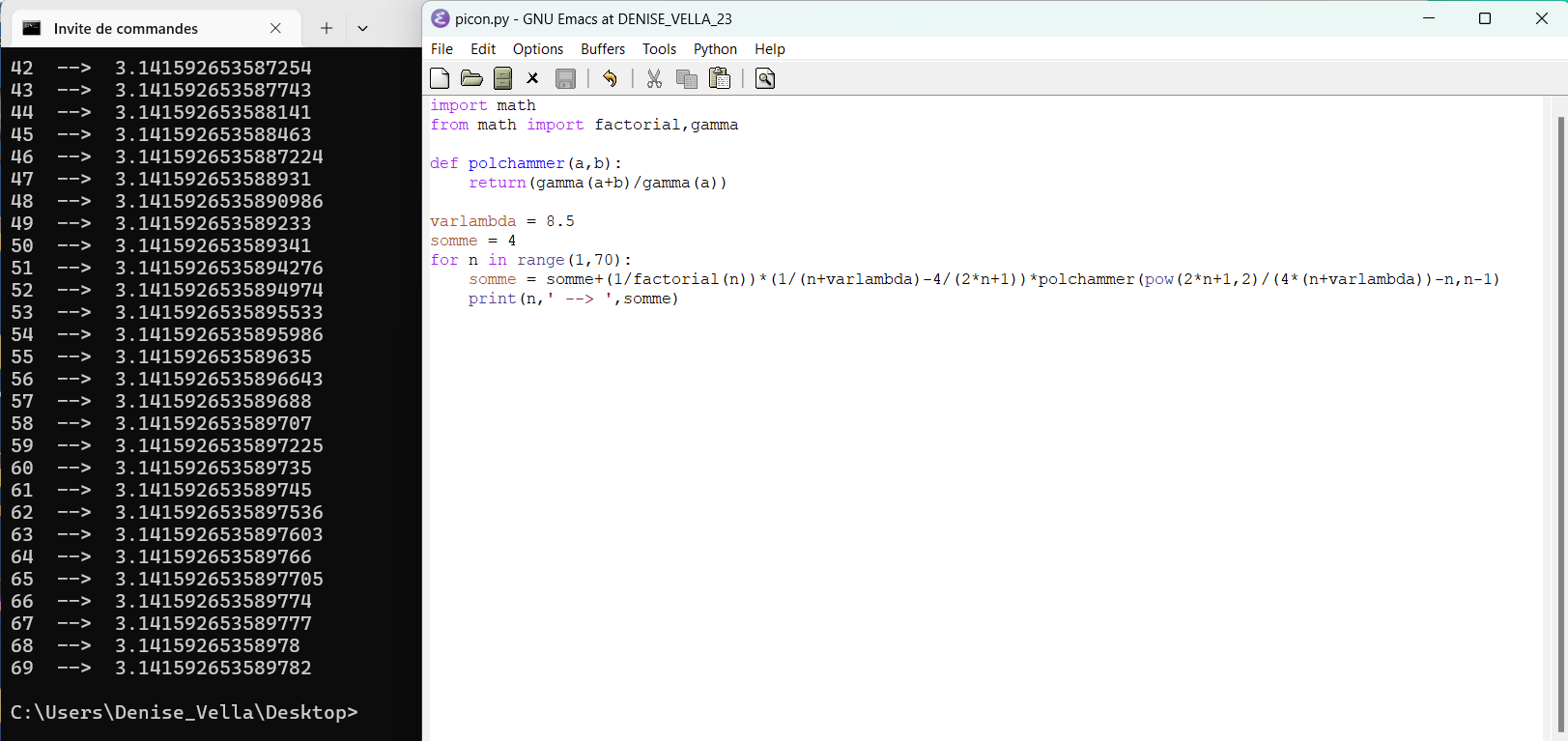 converge très lentement converge très lentement    
-
27.4.2024 : expression d’une assertion impliquant CG dans ℂ (c’est le printemps, nombres grains de pollen) et un tout petit programme qui trouve les nombres premiers (757)
-
27.4.2024 : dans l’introduction de l’article de Gemma de Las Cuevas et al. (
 ), j’ai appris qu’il faut appeler Moments les traces des puissances d’un opérateur, ce sont donc les moments que calculait le programme du 10.7.2019 : ♥ un ensemble, une transformation, des traces de premiers (756) ), j’ai appris qu’il faut appeler Moments les traces des puissances d’un opérateur, ce sont donc les moments que calculait le programme du 10.7.2019 : ♥ un ensemble, une transformation, des traces de premiers (756)  
(si ce n’est que la matrice à multi-circulantes sur la diagonale n’est pas symétrique, et donc, je ne sais pas si le terme Moments s’applique). Patience et longueur de temps font plus que force ni que rage.
-
avril 2024 : calcul d’une formule u(s) sur un tableau à Goutelas (755)
  
-
14.4.2024 : de l’importance d’une phrase (754)
 résultats (nmax = 1M, moyenne, Cesàro, R. Stone) résultats (nmax = 1M, moyenne, Cesàro, R. Stone) 
-
9.4.2024 : Petites expérimentations informatiques autour de quelques zéros de la fonction ζ de Riemann (753)
 11.4.: j’adore ma formule, je l’ai testée avec 1000 zéros et en faisant semblant que l’infini, c’est 1 million, elle est cool ! (programme et résultat) 11.4.: j’adore ma formule, je l’ai testée avec 1000 zéros et en faisant semblant que l’infini, c’est 1 million, elle est cool ! (programme et résultat)  
-
Le i de Galois : référence enfin trouvée, mais trop difficile à comprendre (intégrales elliptiques) (752)
  Petit extrait de Meissel dans lequel on trouve aussi cette formule, mais sans le i de Galois (page 5/12) Petit extrait de Meissel dans lequel on trouve aussi cette formule, mais sans le i de Galois (page 5/12) 
-
27.3.2024 : fêter le π-day avec 13 jours de retard (750)
 7 avril, amélioration : sans complexe ou avec 7 avril, amélioration : sans complexe ou avec 
-
23.3.2024 : suivre à nouveau van der Pol (749)

-
18.3.2024 : Have fun ! Nombres premiers et tortue Logo (748)

-
mars 2024 : Tests des théorèmes de Mertens (747)

-
mars 2024 : Une rencontre simple de l’inverse de la racine de 2 (746)

-
mars 2024 : Transcription en LaTeX de la Section troisième des Recherches arithmétiques de Carl Friedrich Gauss
 
-
♥♥ 22.2.2024 : exponentielle et logarithme : Des intérêts composés (petit encart devoir d’Évariste, et dédicace spéciale à grand-papa Lulu, qui m’a appris à factoriser, et le célèbre holorime aussi) (745)
 étonnement constant étonnement constant  Compléments par Pierre de la Harpe Compléments par Pierre de la Harpe  de ce fait, image du résultat d’un programme python d’expression du log par une racine "beaucoup"-ième de ce fait, image du résultat d’un programme python d’expression du log par une racine "beaucoup"-ième    
-
27.2.2024 : 2 extraits des Werke de Carl Friedrich Gauss et une lettre (traduits du latin ou de l’allemand, autant que faire se peut) : Quarumdam serierum singularium
 Lettre de Encke à Gauss du 4 décembre 1849 Lettre de Encke à Gauss du 4 décembre 1849  
somme des cos et sin des résid. quad.  tests tests 
-
6.2.2024 : Alain Connes à l’Académie des Sciences : Mathématiques et imagination, transcription
 également transcription de la vidéo à l’Académie en 2006 également transcription de la vidéo à l’Académie en 2006  et transcription de la vidéo à l’Académie en 2011 et transcription de la vidéo à l’Académie en 2011  
-
février 2024 : tentative de traduction (google) à partir de l’allemand de la fameuse lettre de Goldbach à Euler du 7 juin 1742

-
février 2024 : E.T. retourner... (je mets ce titre car cette traduction de Murray Shanahan : Parler des grands modèles de langage (LLM) est un retour aux sources de 1989)

-
janvier 2024 : Snurpf et plan complexe (744)
 compléments compléments  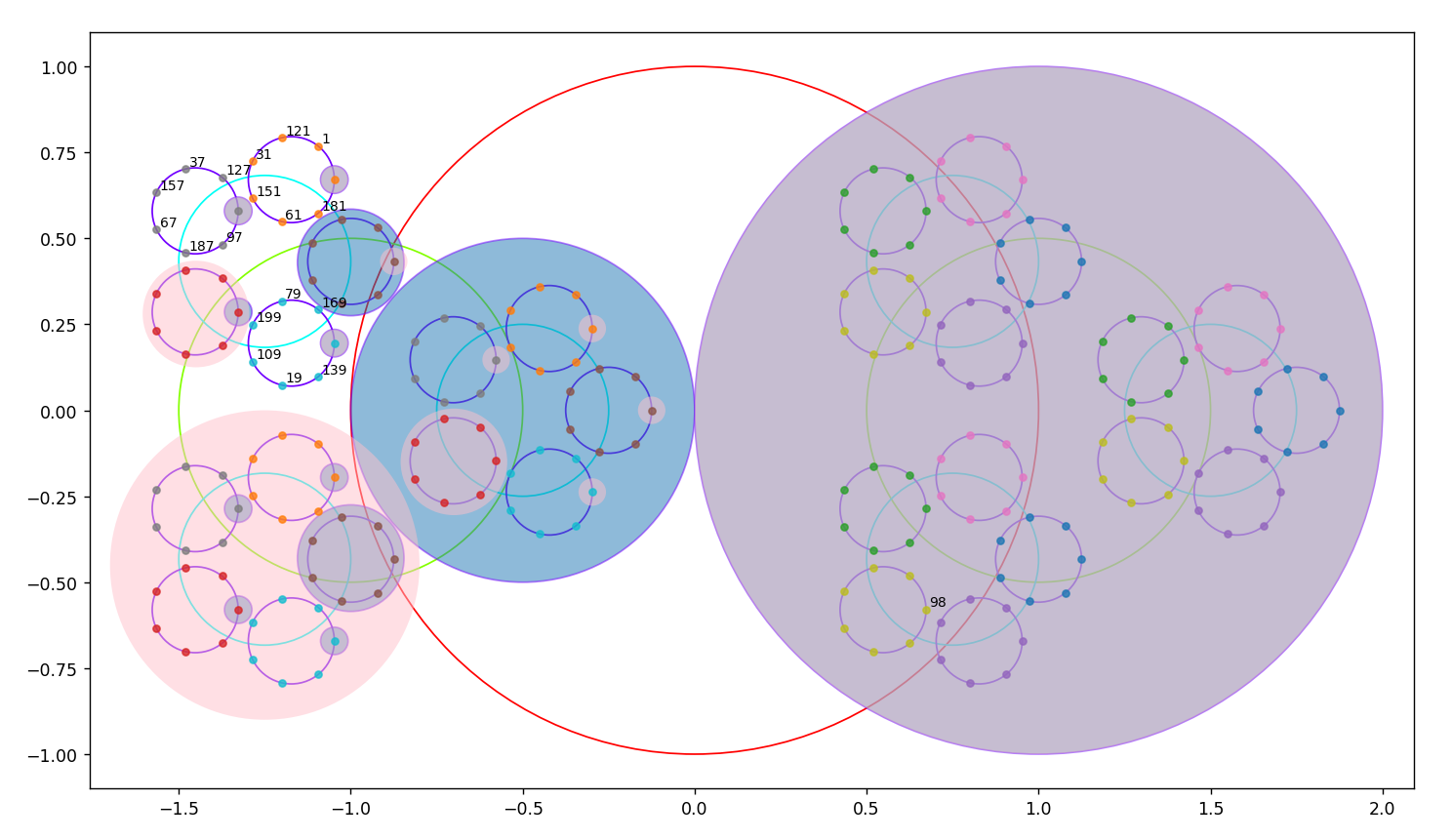 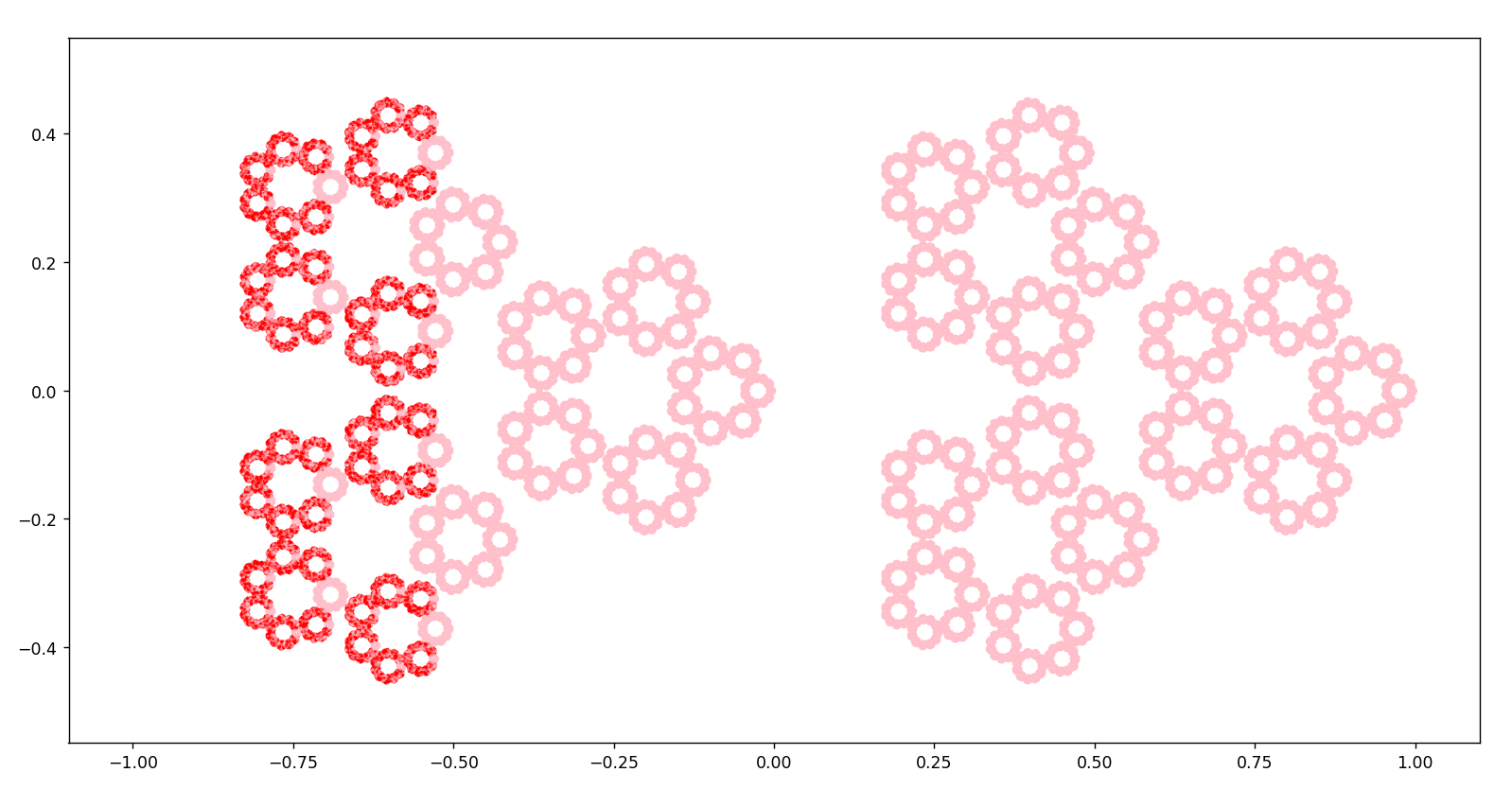 criblage par premiers décroissant jusqu’à 210 criblage par premiers décroissant jusqu’à 210 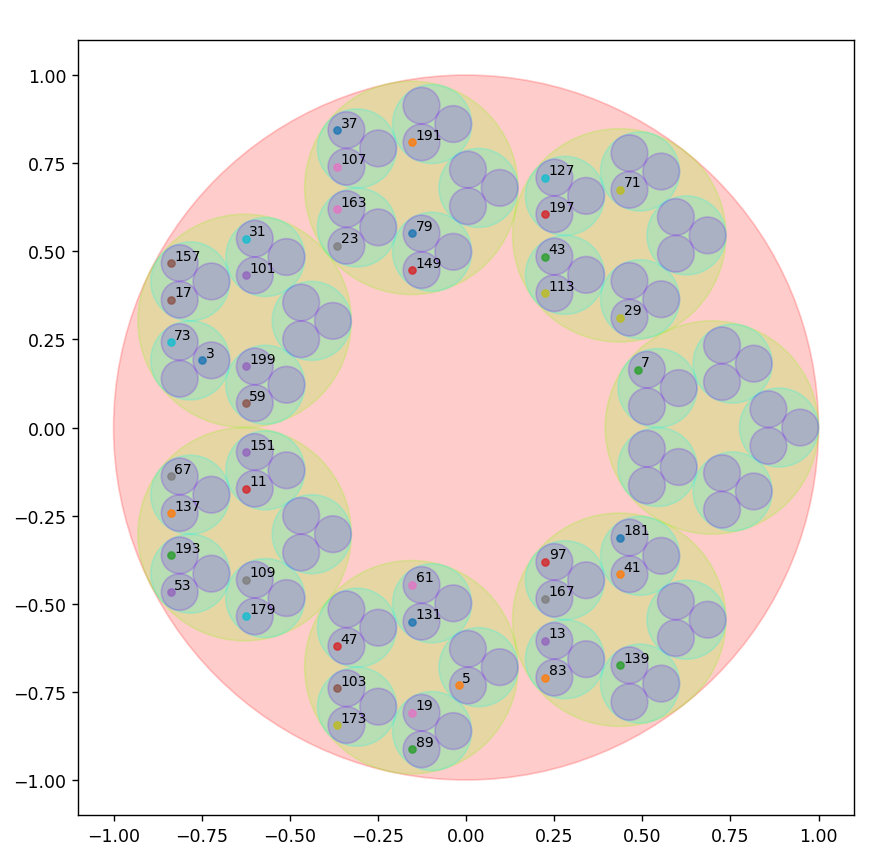
-
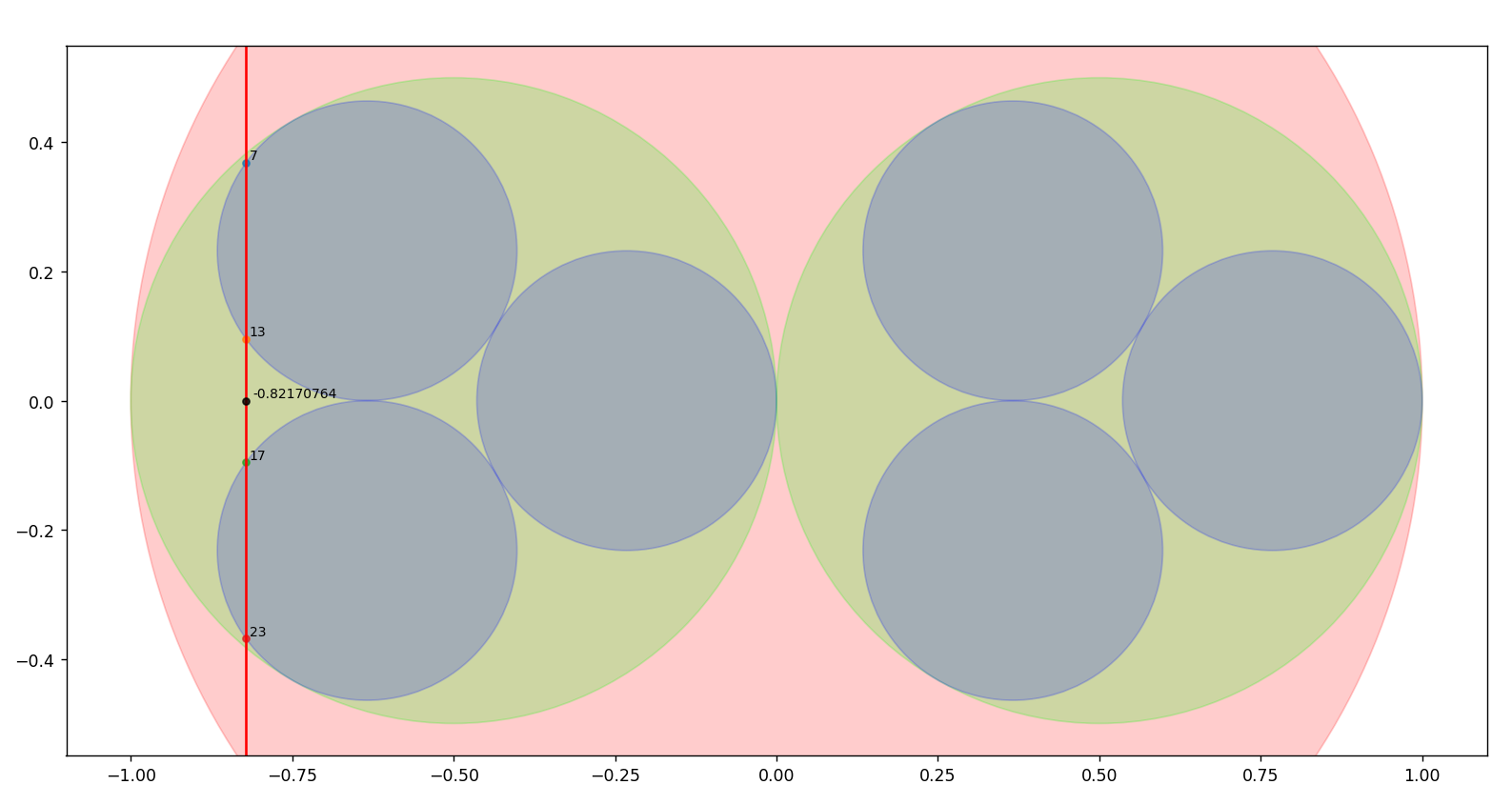
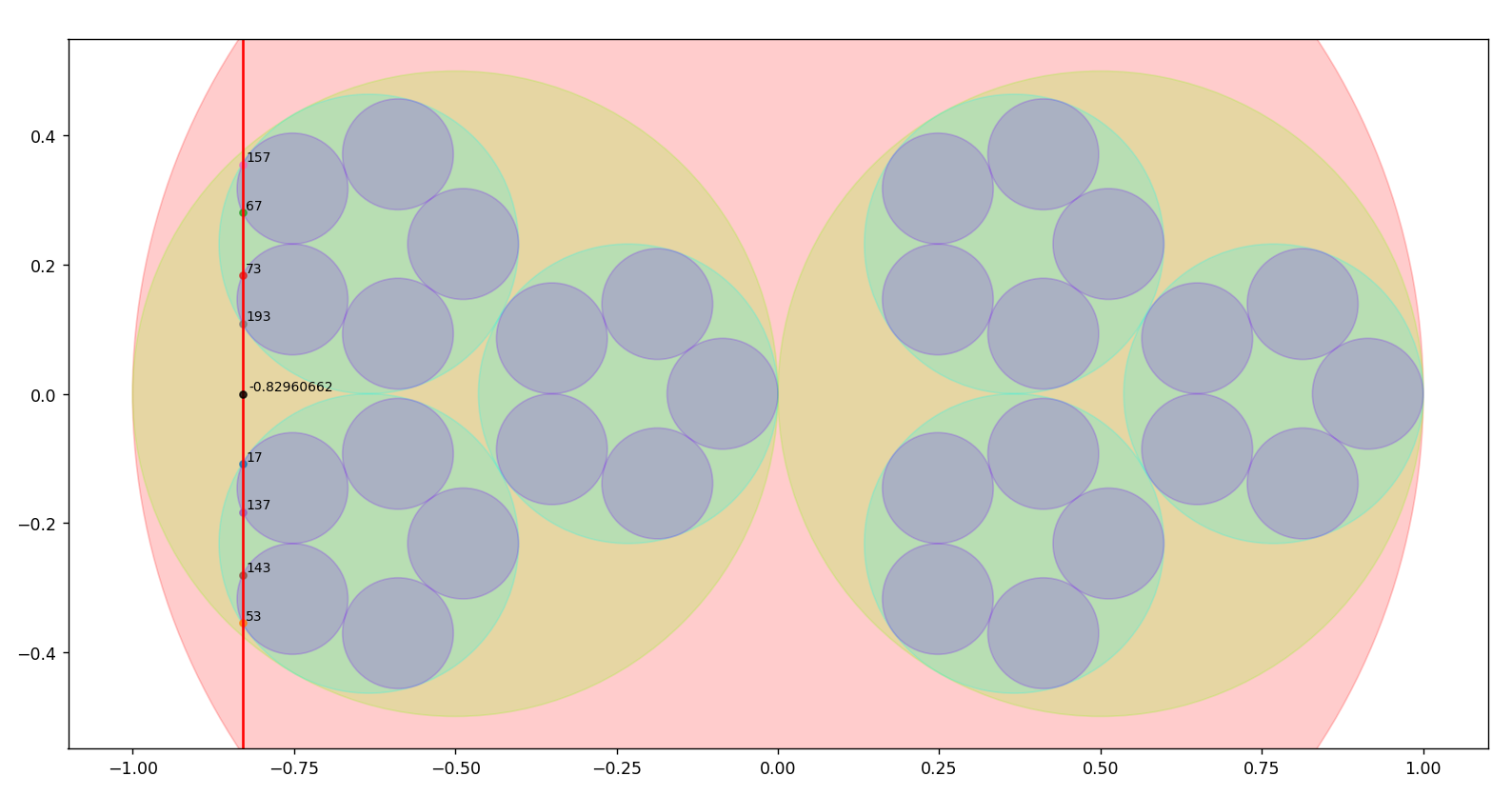
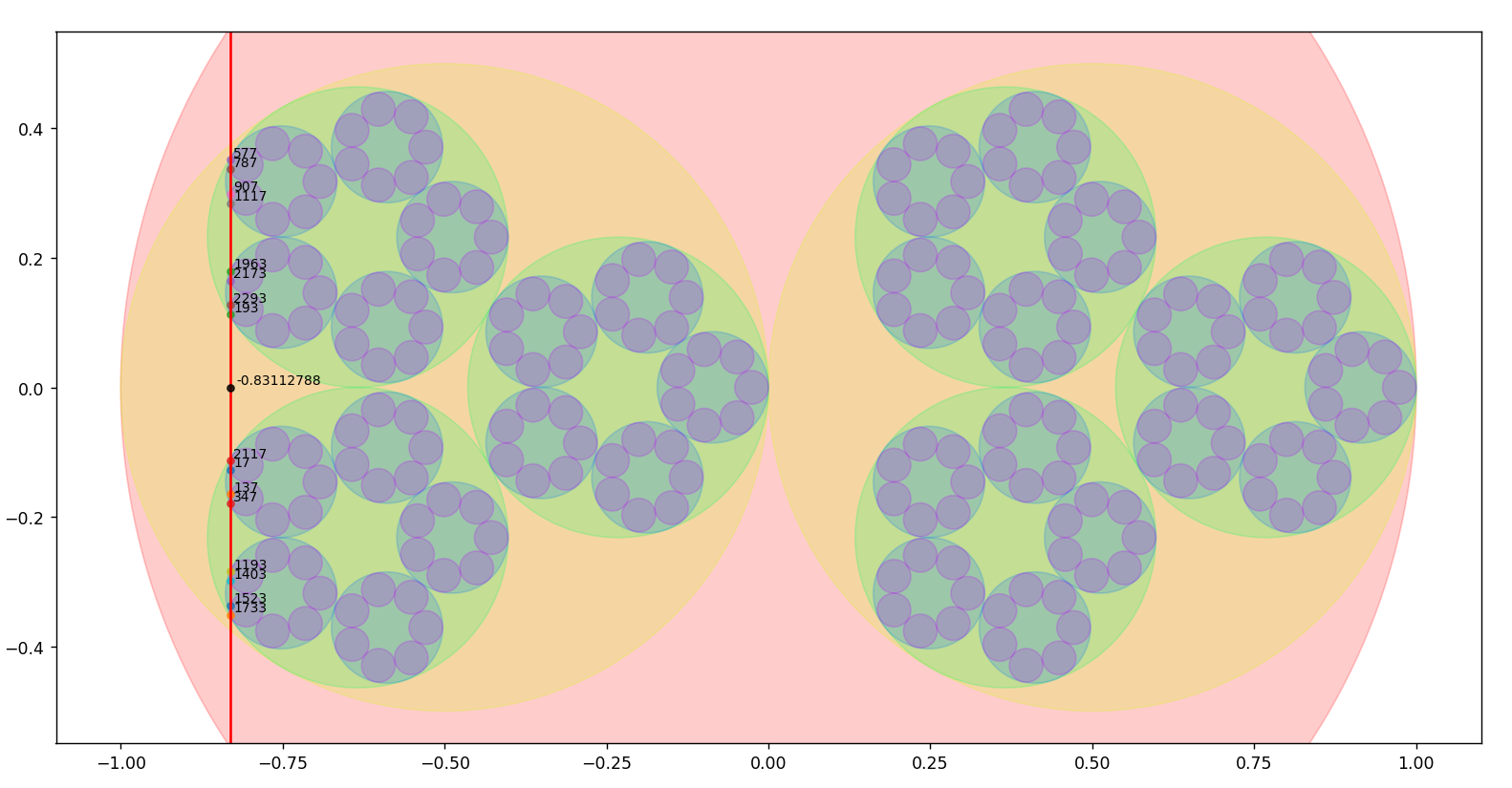
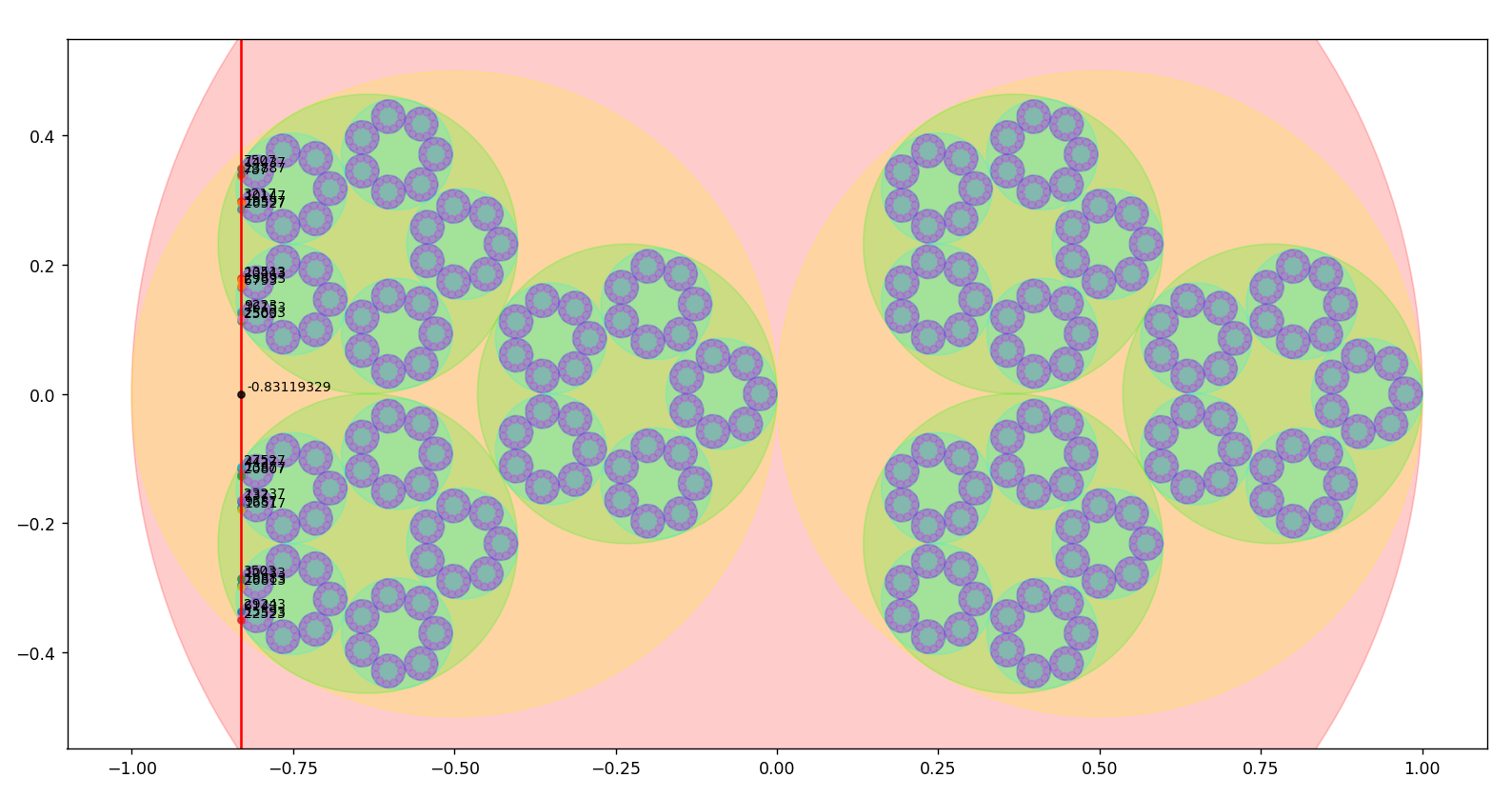
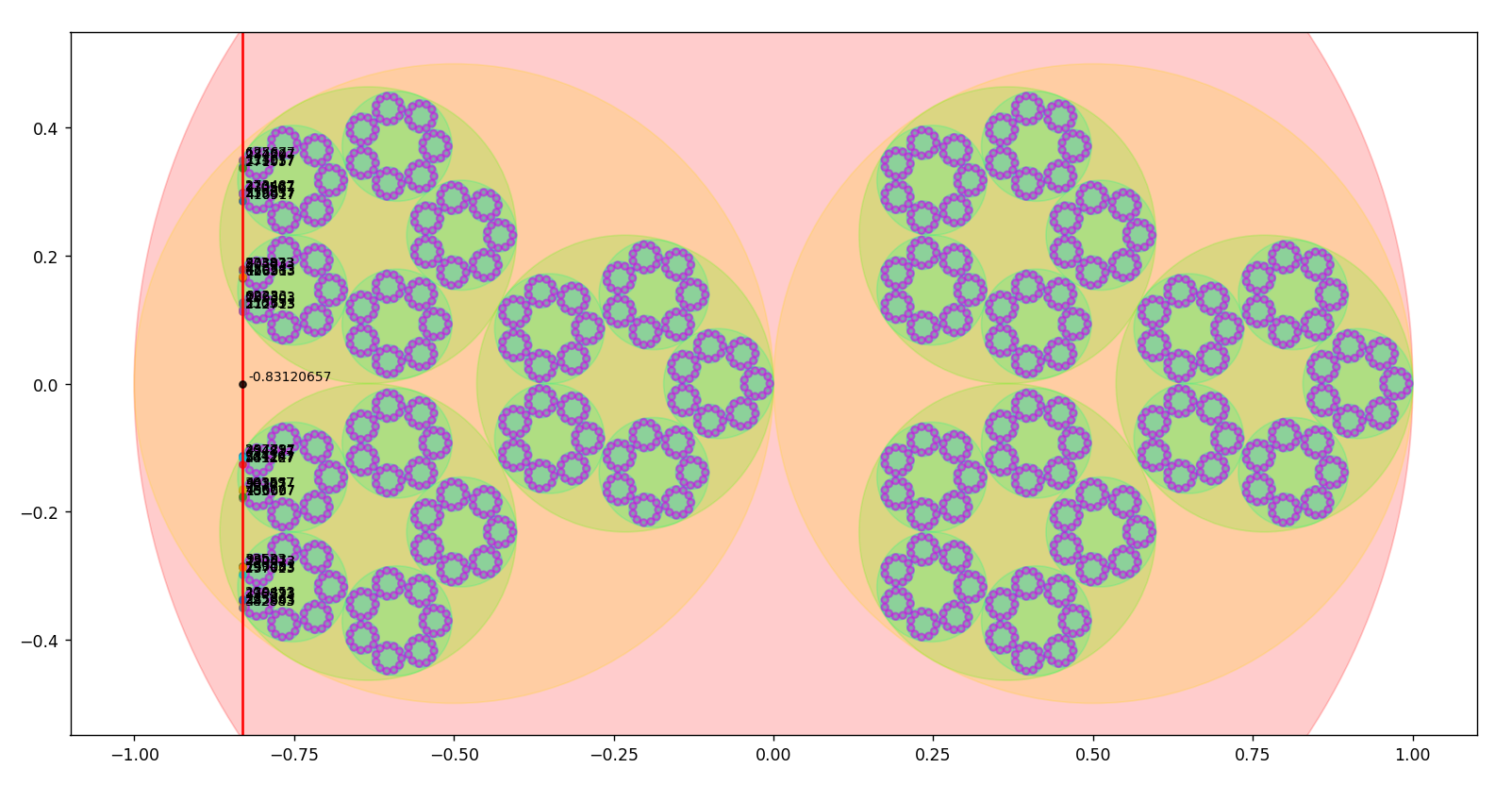
14.1.2024 : On place les nombres selon le Snurpf (système de numérotation par les restes dans les parties finies de ℕ) sur le plan complexe dans des disques de plus en plus petits. Le programme permet d’aller jusqu’à la primorielle de 17 qui vaut 2 x 3 x 5 x 7 x 11 x 13 x 17=510510.
On calcule la limite des positionnements à gauche et on dirait que les parties réelles des positionnements tendent vers -0.8312072615486259... (calcul jusqu’au vingtième nombre premier qui est 71) (743)
-
janvier 2024, poursuite de la transcription en Latex des textes de É. Galois : texte fondateur sur la résolubilité par radicaux des équations
 articles du Bulletin des sciences mathématiques de Férussac articles du Bulletin des sciences mathématiques de Férussac  Lettre à M. Auguste Chevalier Lettre à M. Auguste Chevalier  Fragment d’un second mémoire Fragment d’un second mémoire   
-
8.11.2023 : bidominos bicolores (742)

-
4.11.2023 : des nombres qui en permutent d’autres (741)
 utilisation de permutations à la recherche de décompositions de Goldbach utilisation de permutations à la recherche de décompositions de Goldbach 
-
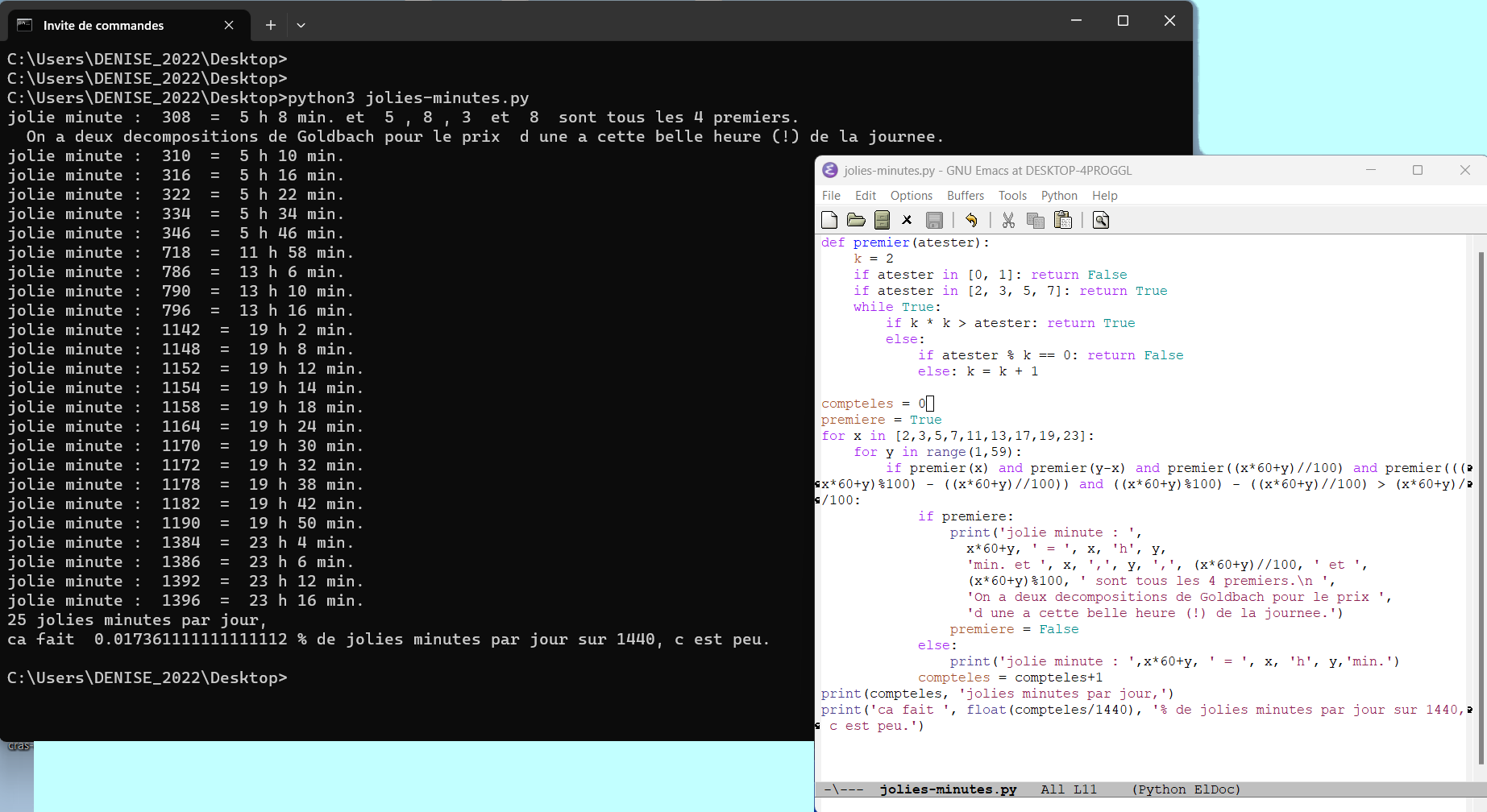
9.9.2023 : les jolies minutes de la journée (740)
-
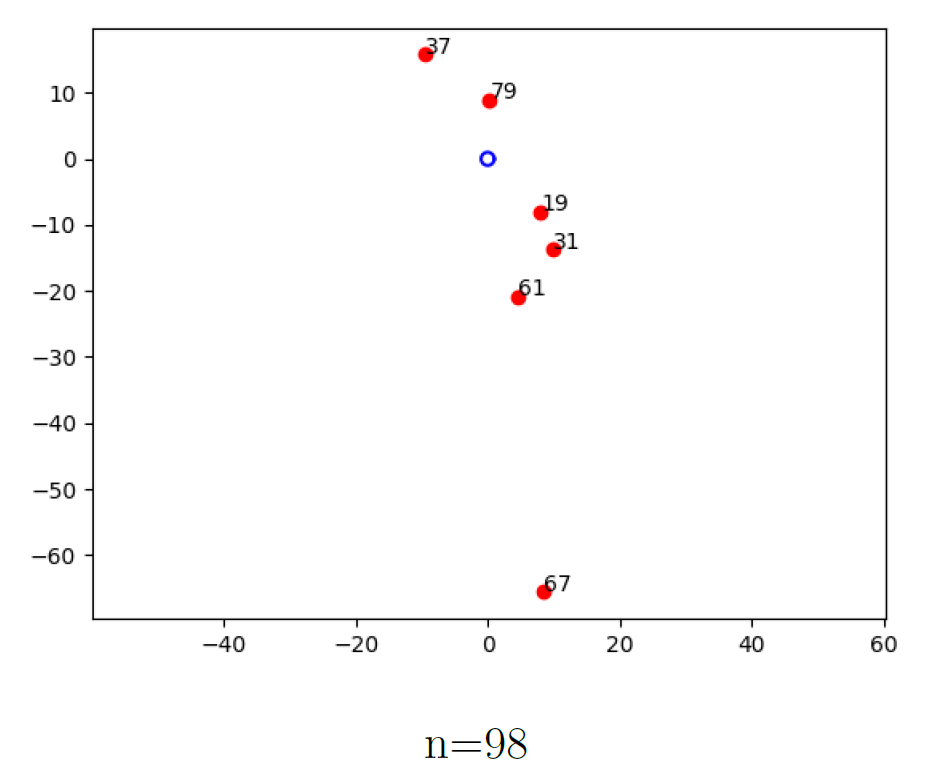
26.8.2023 : ils semblent bien maximiser une distance... (739)

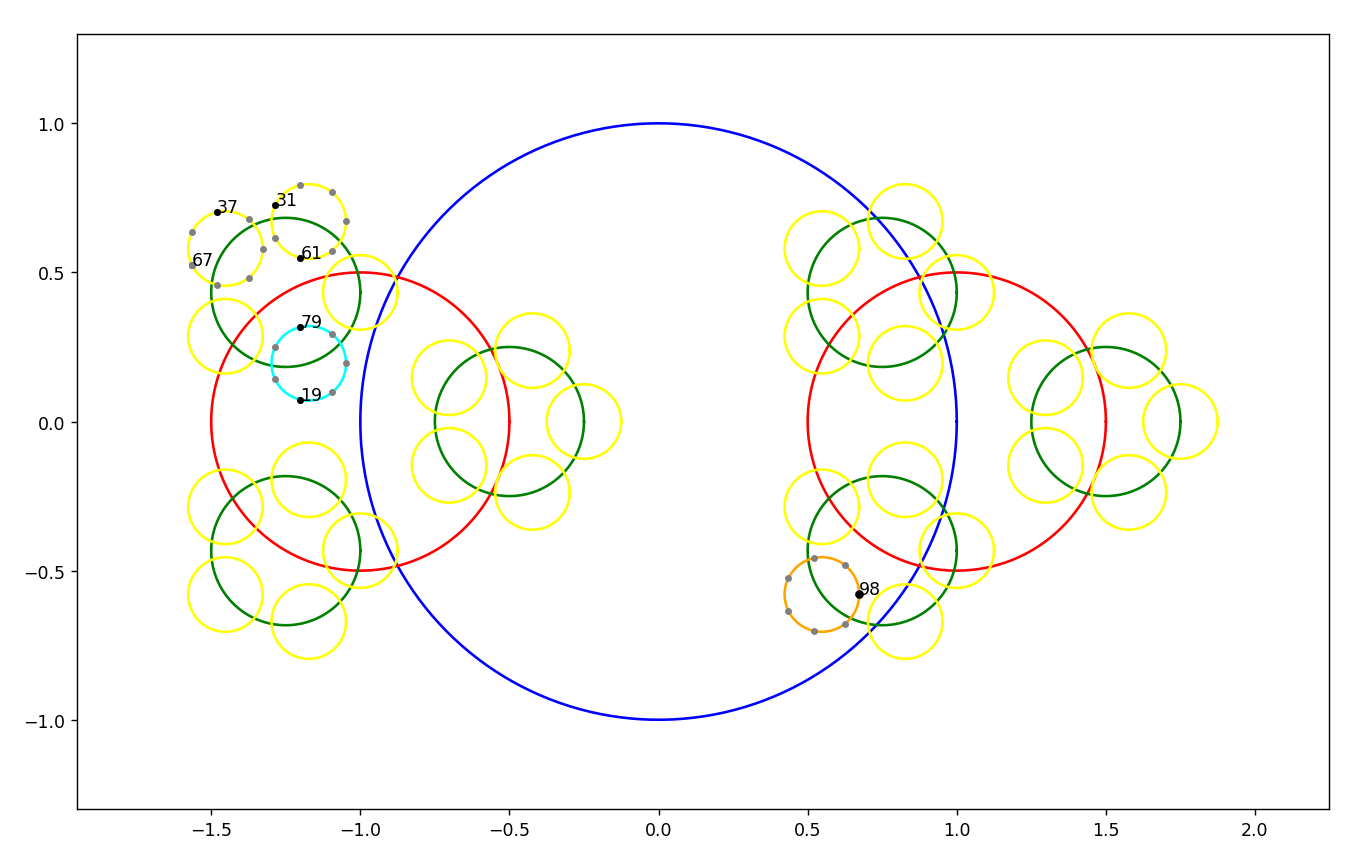 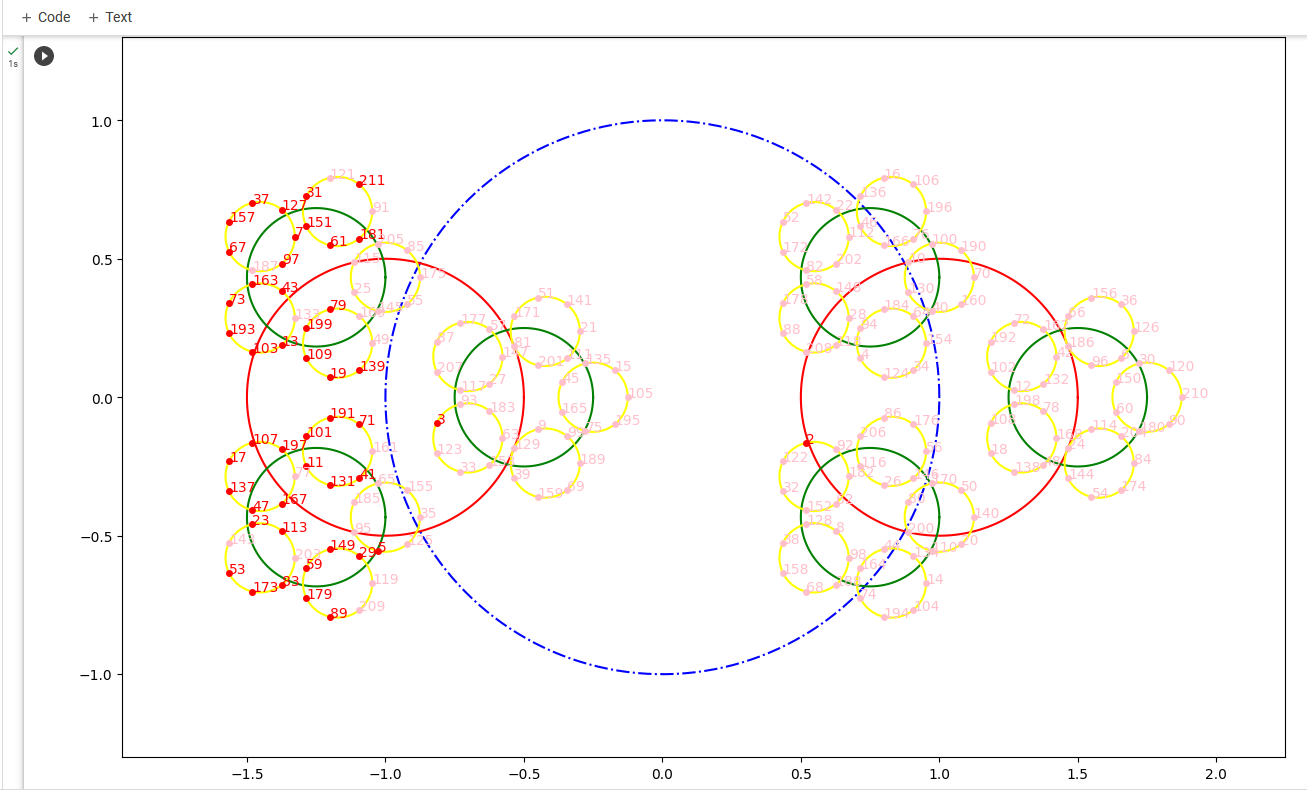 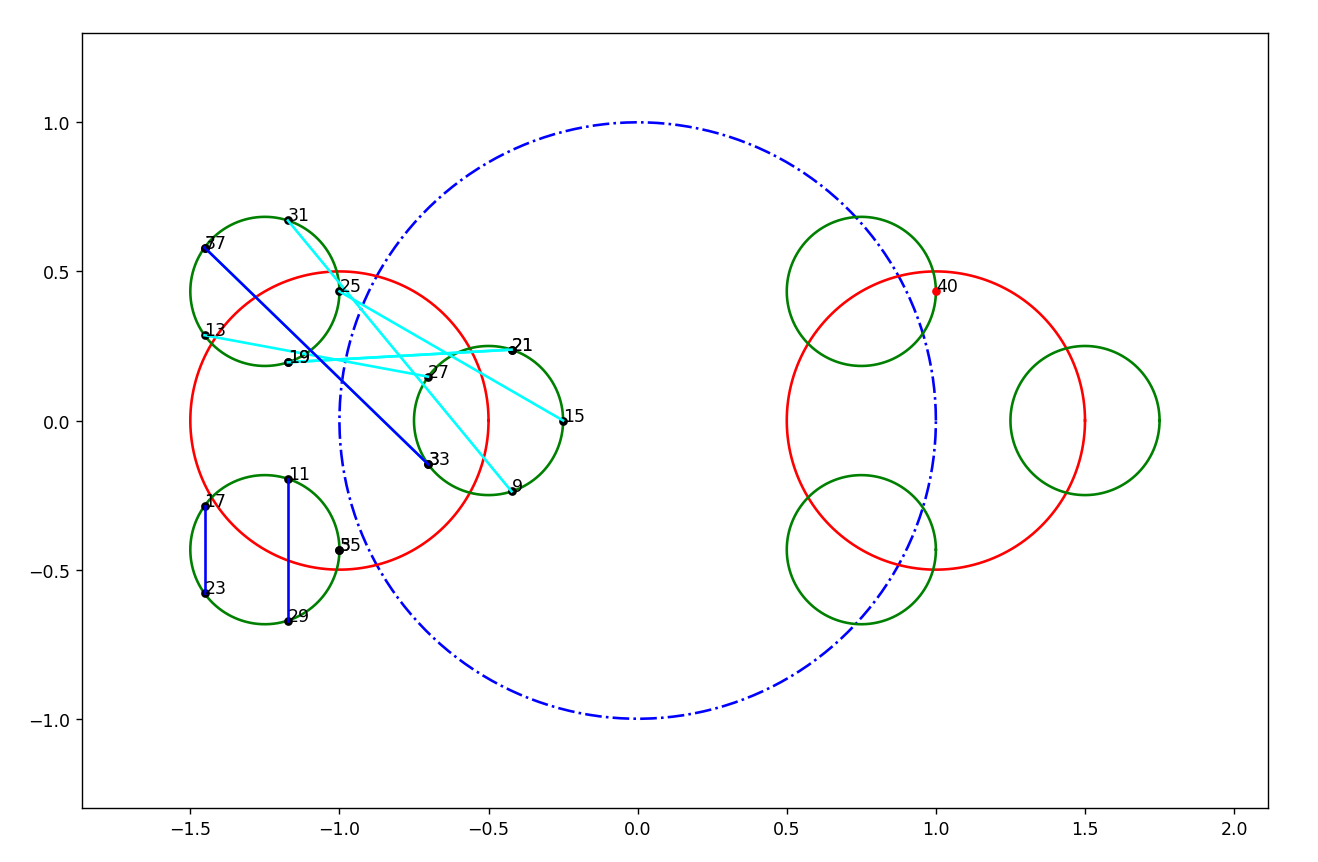 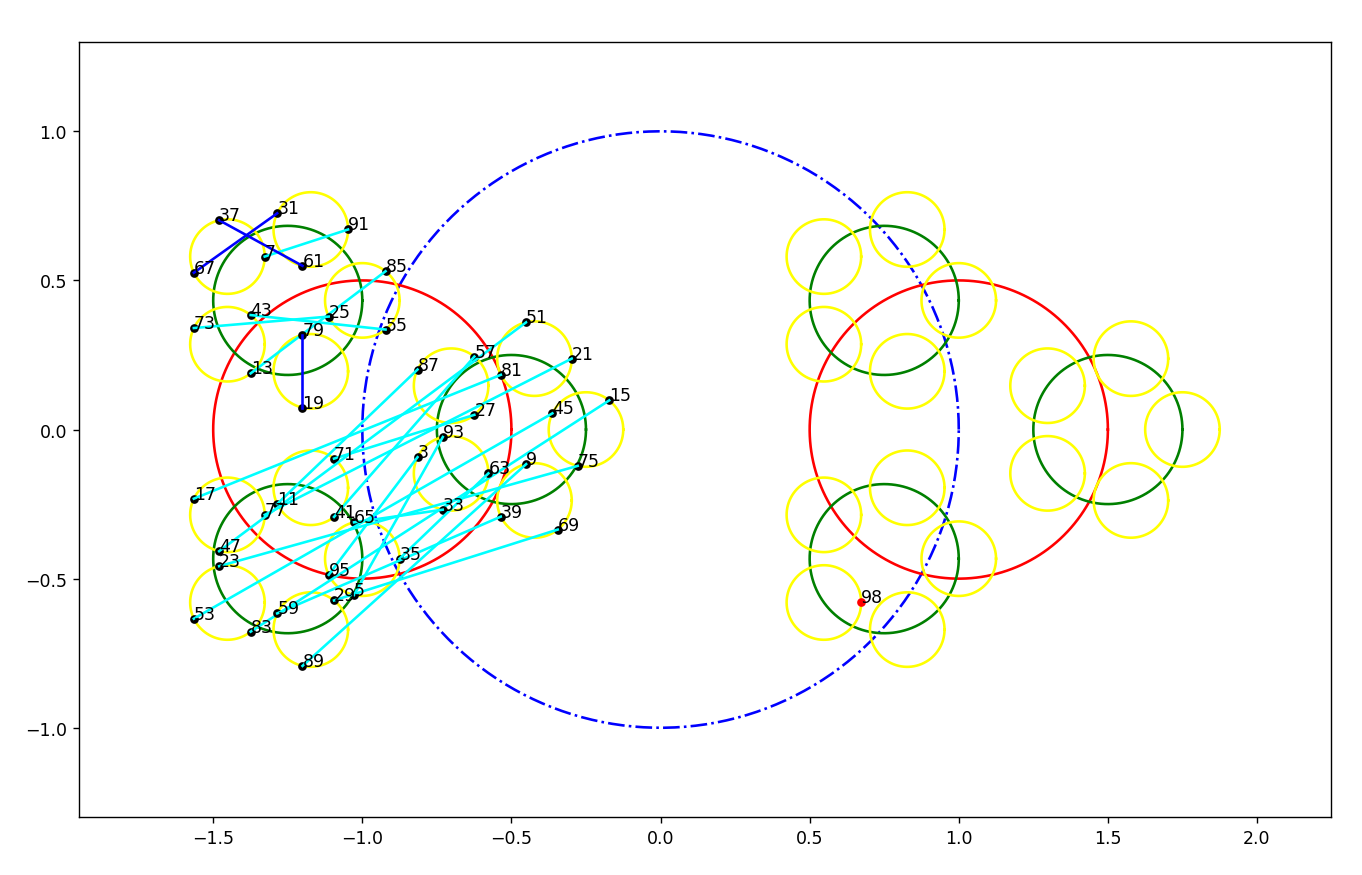 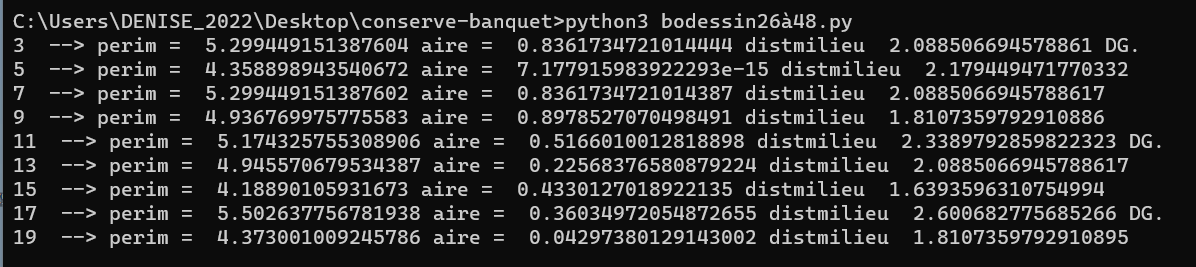 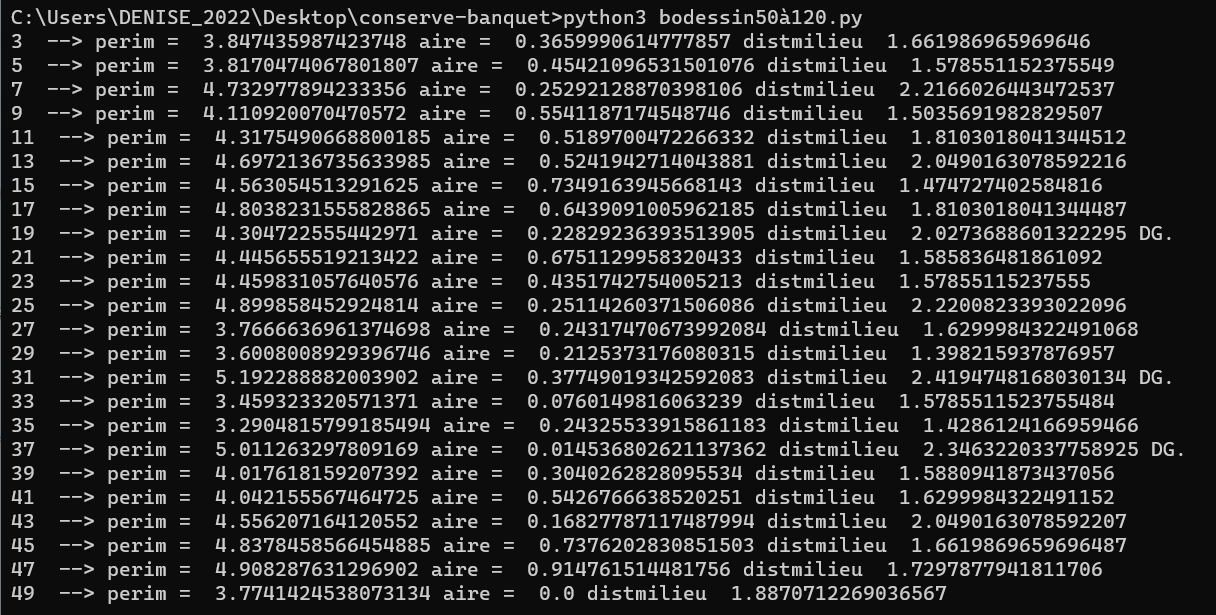 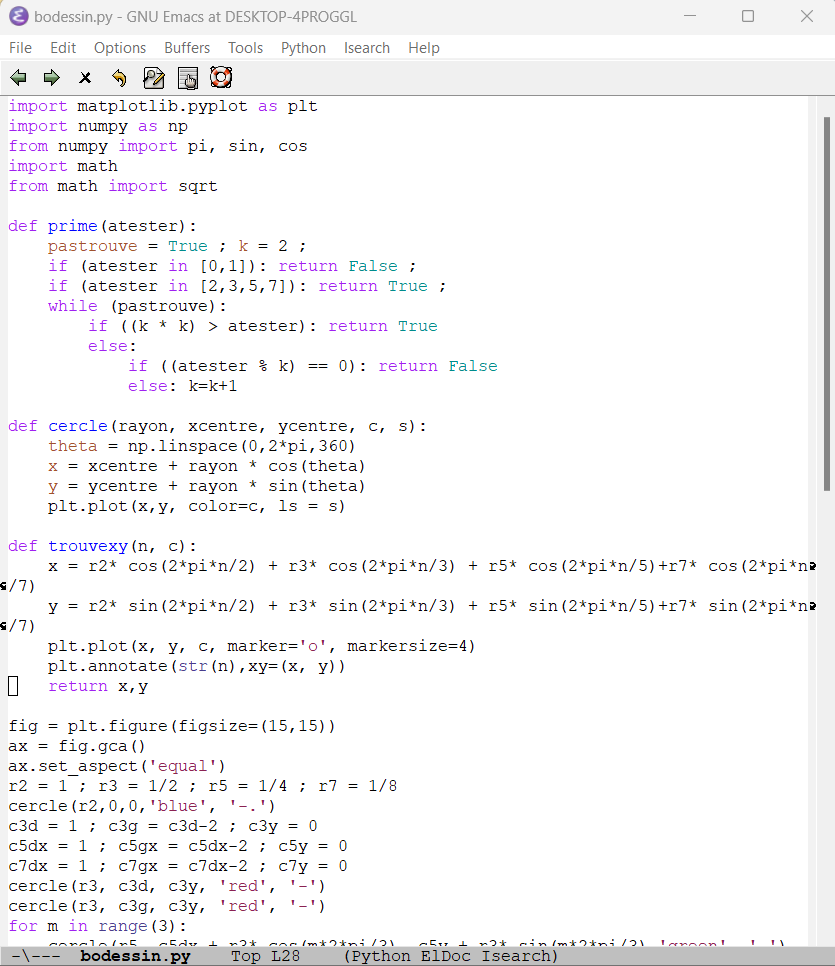 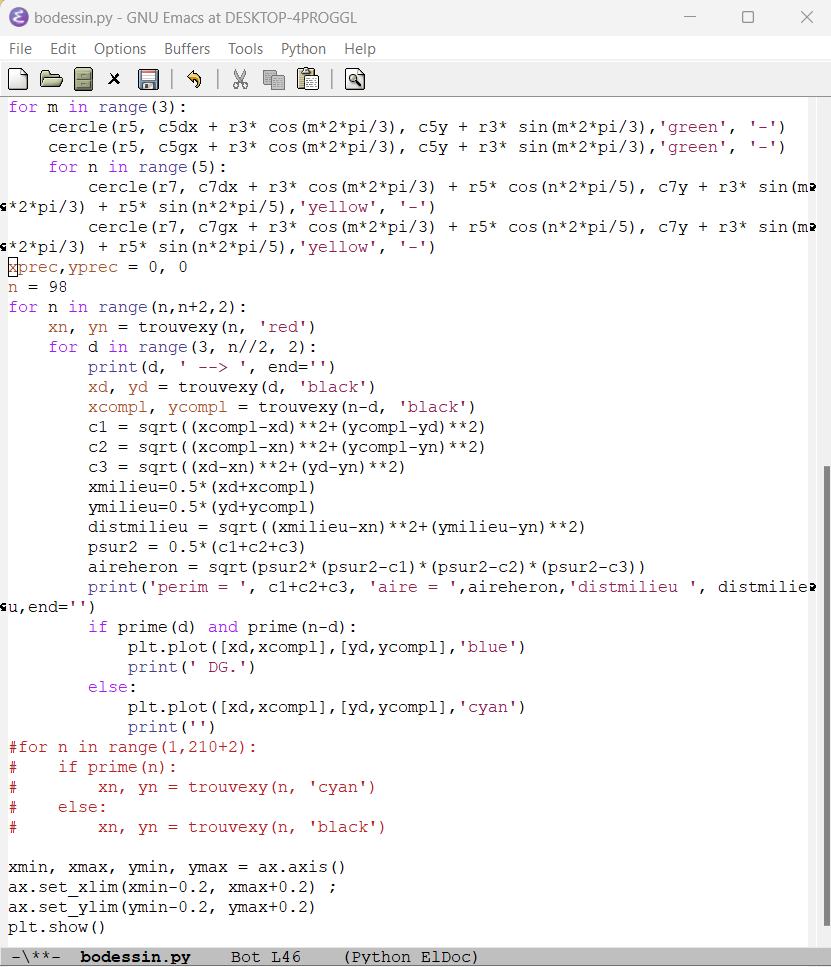
Pour n=40, les 3 décompositions de Goldbach maximisent la distance de n au milieu du segment reliant les deux décomposants, pour 98, 31 et 37 maximisent la distance en question, mais pas 19.
Programme plus court ;-) et positionnement des nombres jusqu’à 2.3.5.7 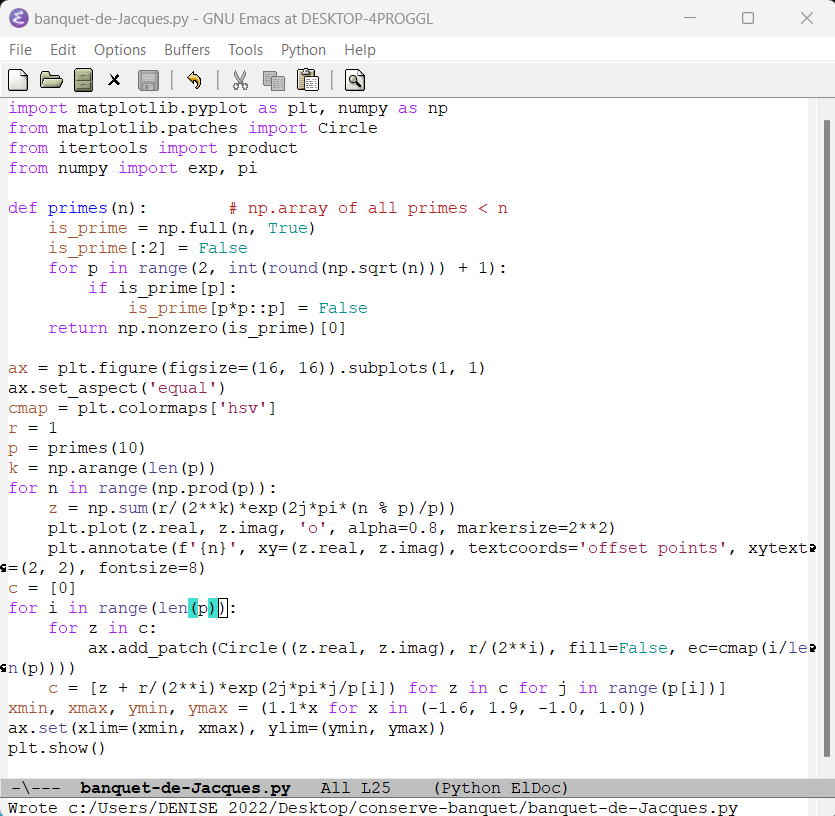 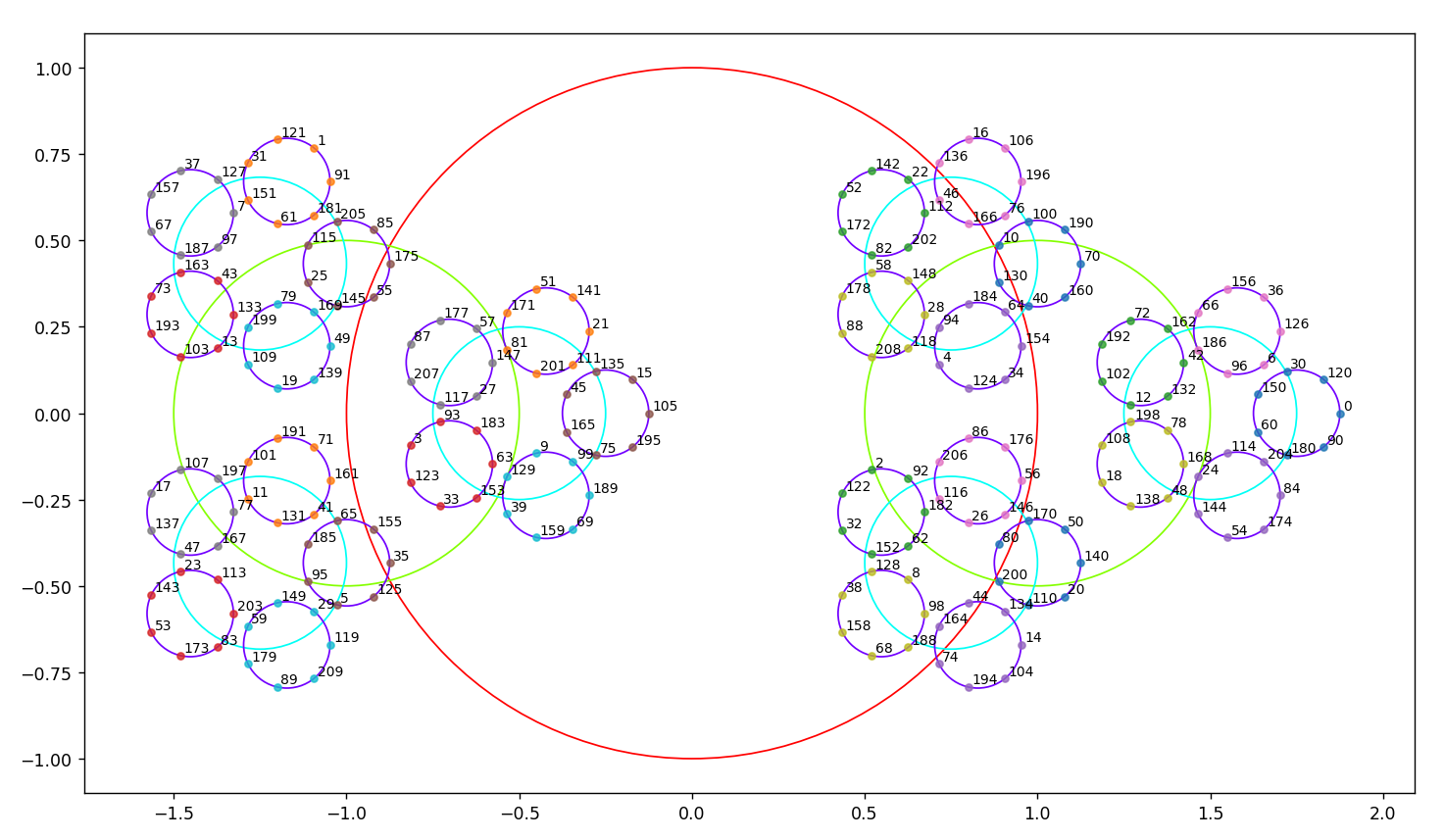
-
19.8.2023 : découverte, peut-être, d’une piste géométrique pour la conjecture de Goldbach, en lien avec les puissances de 2 et 3 (738)

-
août 2023 : petite remarque sur les systèmes de numération (737)

-
rappel des programmes des enveloppes par des droites (736)

-
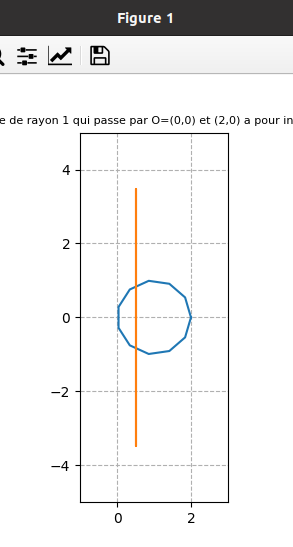
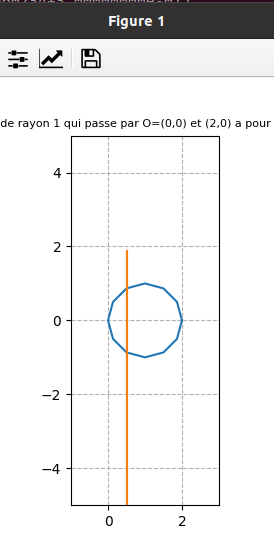
août 2023 : envoyer les solutions Goldbach du cercle-unité centré en 1 sur la droite critique par inversion !
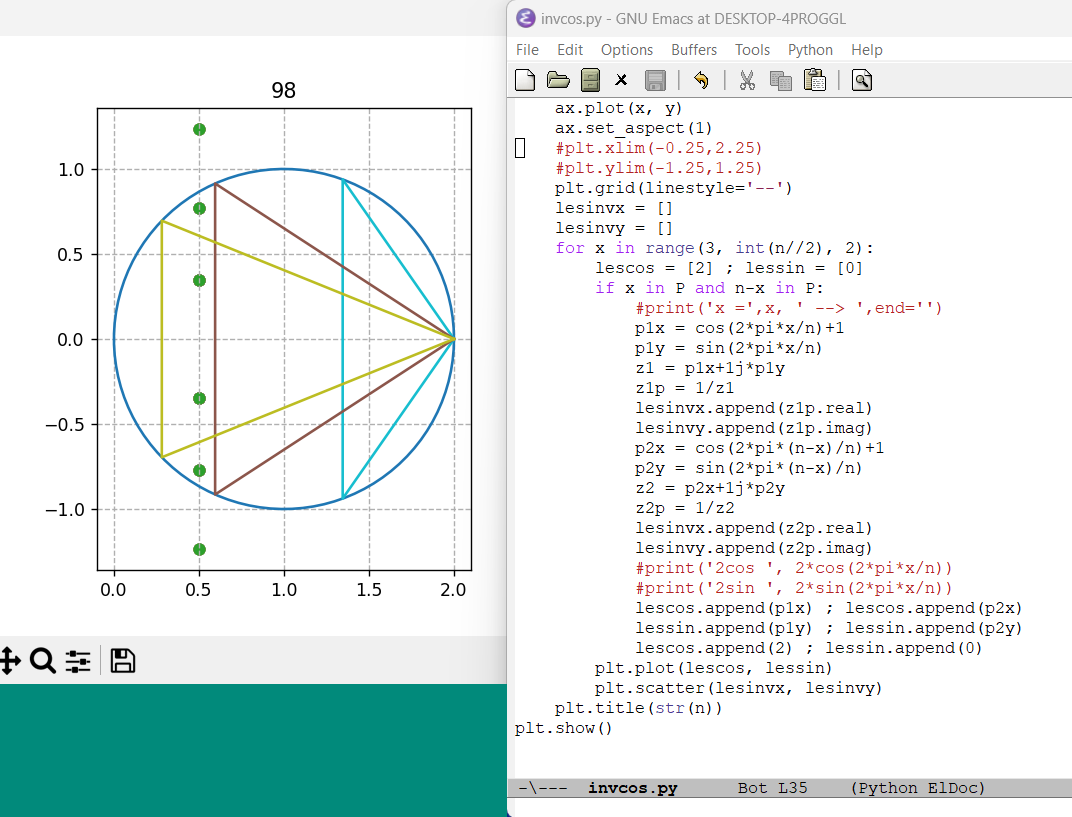
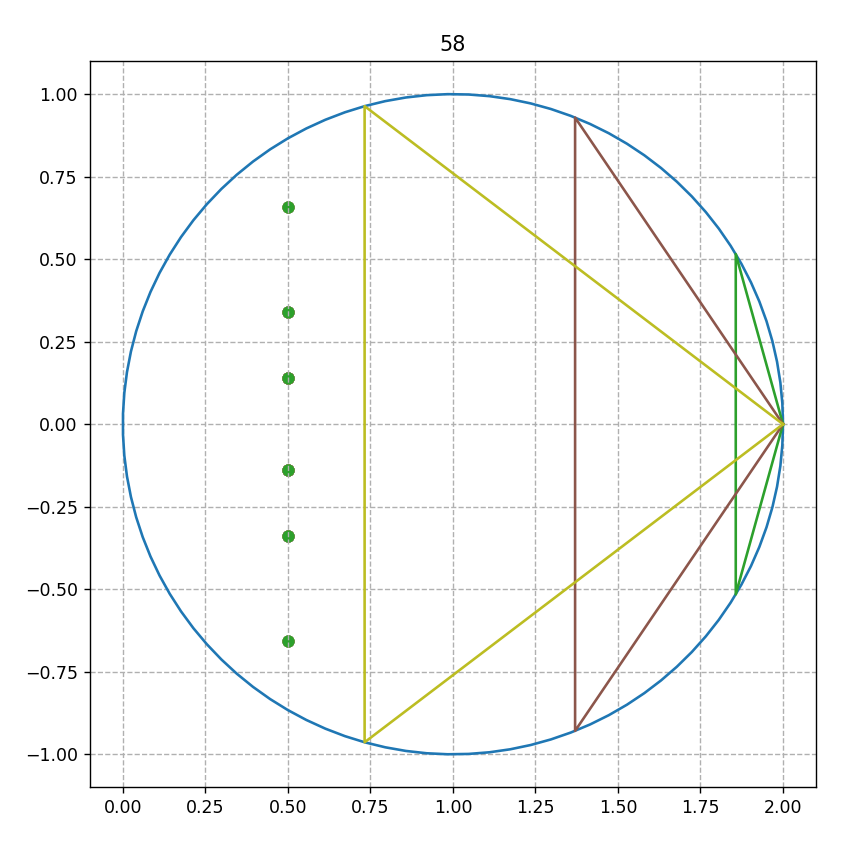
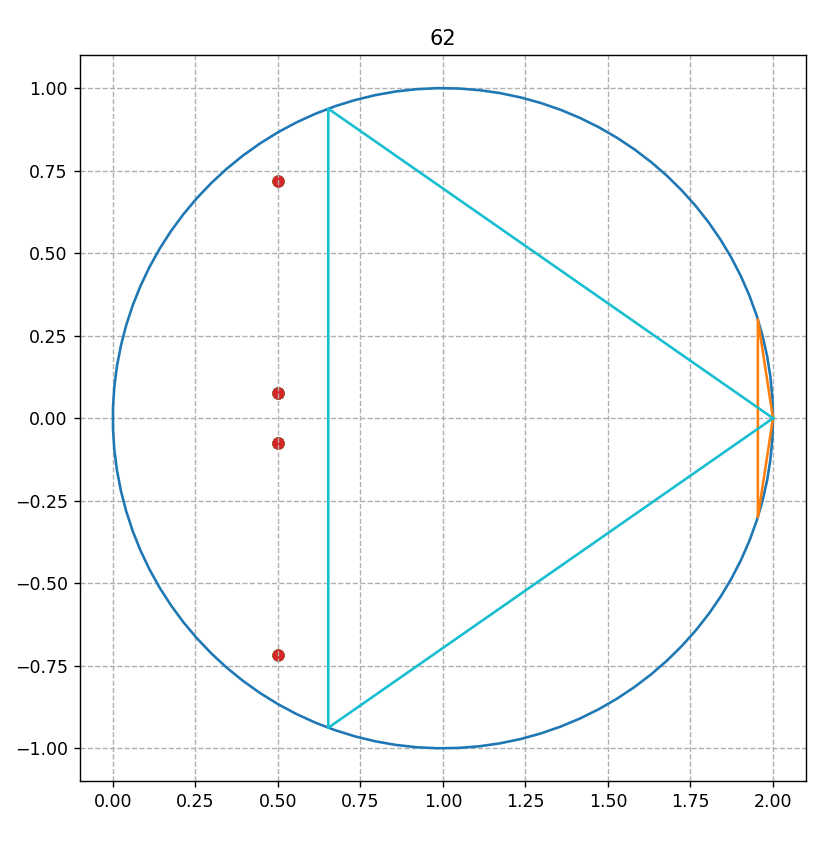
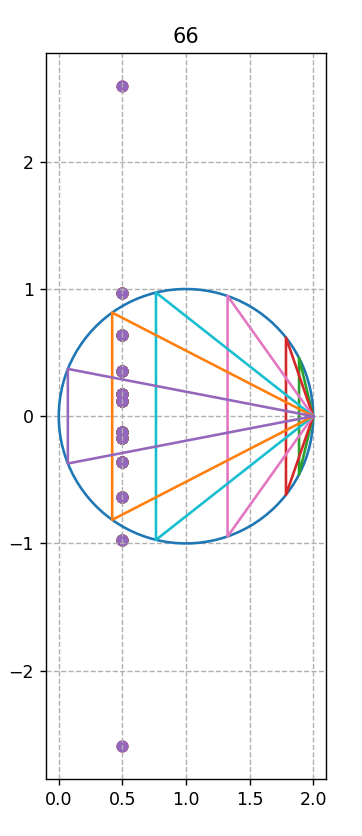
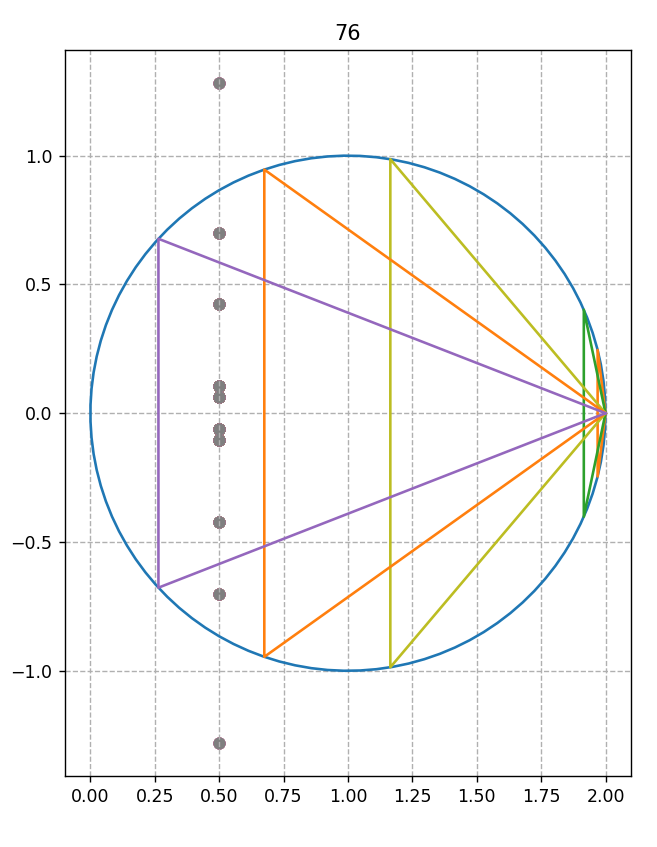 Juin 2023 : explication de ce phénomène découvert en juin 2021 (voir lien vers un article Fun) que l’inverse du cercle-unité décalé à droite (de diamètre [0,2]) est la droite des complexes de partie réelle 1/2 (735)
Juin 2023 : explication de ce phénomène découvert en juin 2021 (voir lien vers un article Fun) que l’inverse du cercle-unité décalé à droite (de diamètre [0,2]) est la droite des complexes de partie réelle 1/2 (735) 
-
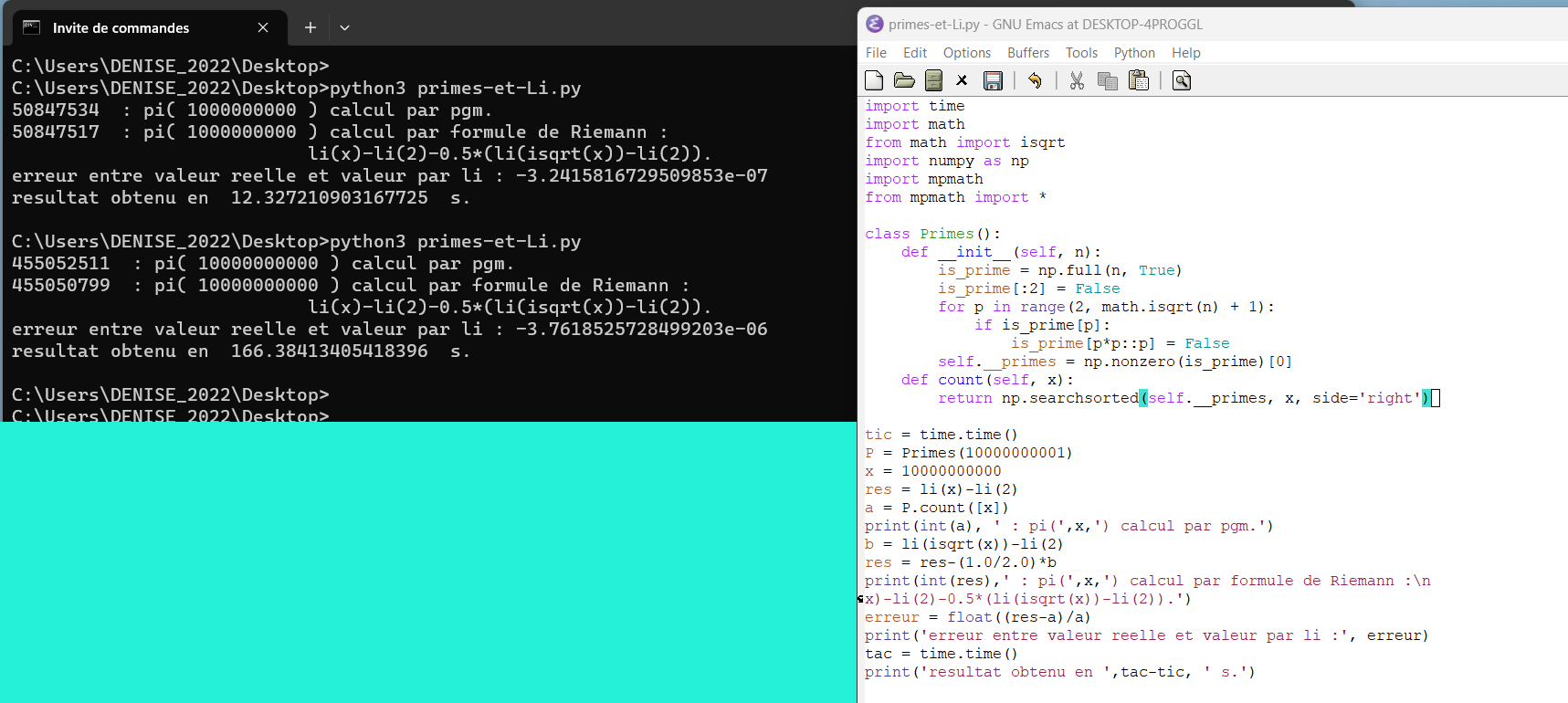
août 2023 : reprise de l’émerveillement de juillet 2017 devant la formule de Riemann faisant intervenir le logarithme intégral avec un programme python plus efficace (734)
-
août 2023 : retour aux valuations p-adiques, en lien avec les travaux récents (de l’importance de l’ordre dans lequel on écrit les arguments d’une fonction, en programmation : hier, ma fonction de calcul de la valuation p-adique était fausse, archi-fausse, j’avais interverti les 2 variables passées à la fonction v(k, x) dans l’appel récursif, et c’est là que la chance intervient : des causes différentes pouvant parfois produire les mêmes effets, ça calculait quand même bien π(x), c’est fou !) (733)
 fourvoiement encore : j’ajoute 1 sur les premiers et un epsilon minuscule sur les autres, c’est normal que ça calcule π(x)... fourvoiement encore : j’ajoute 1 sur les premiers et un epsilon minuscule sur les autres, c’est normal que ça calcule π(x)...
-
juillet 2023 : résumé (732)

-
juillet 2023 : fractales d’anneaux de polynômes (731)
     
-
juillet 2023 : spirale d’Archimède (730)
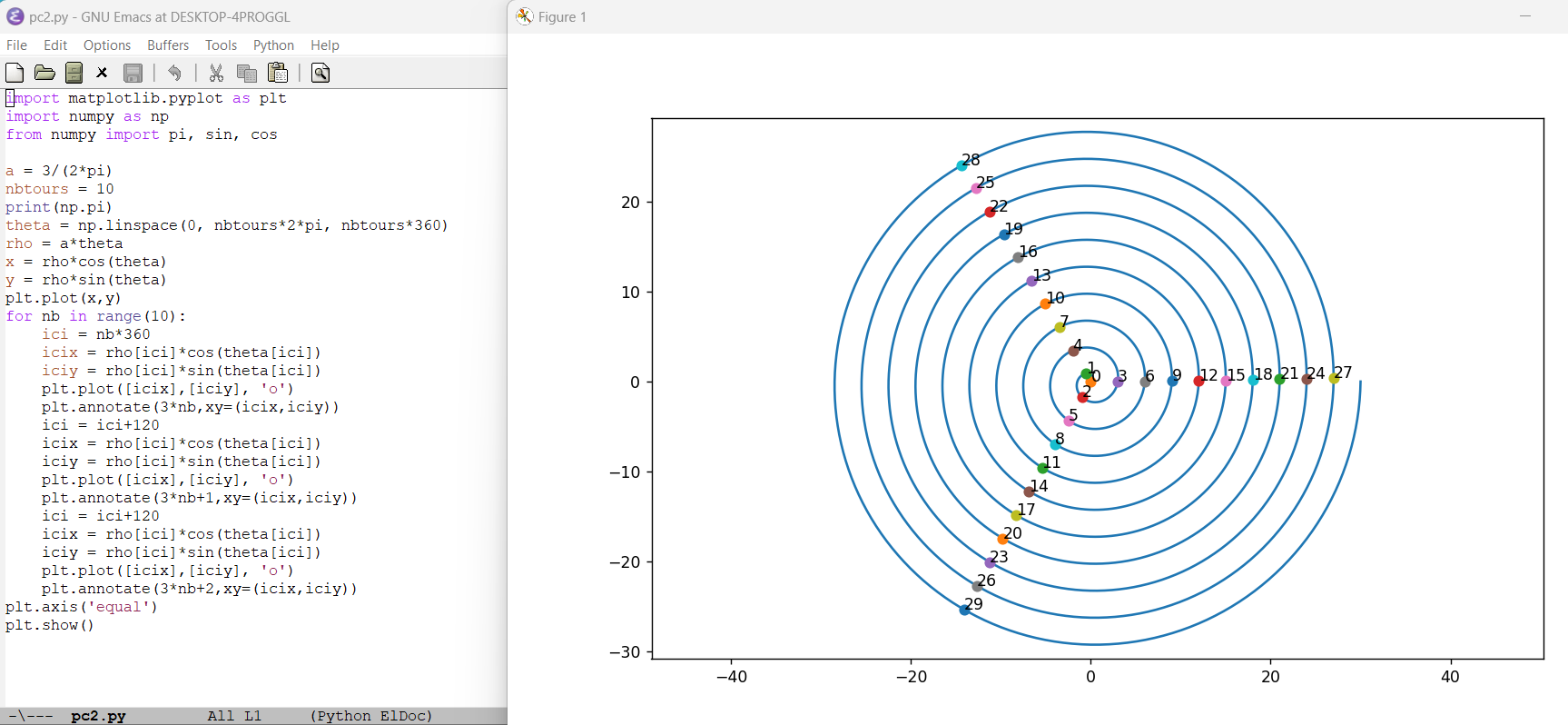 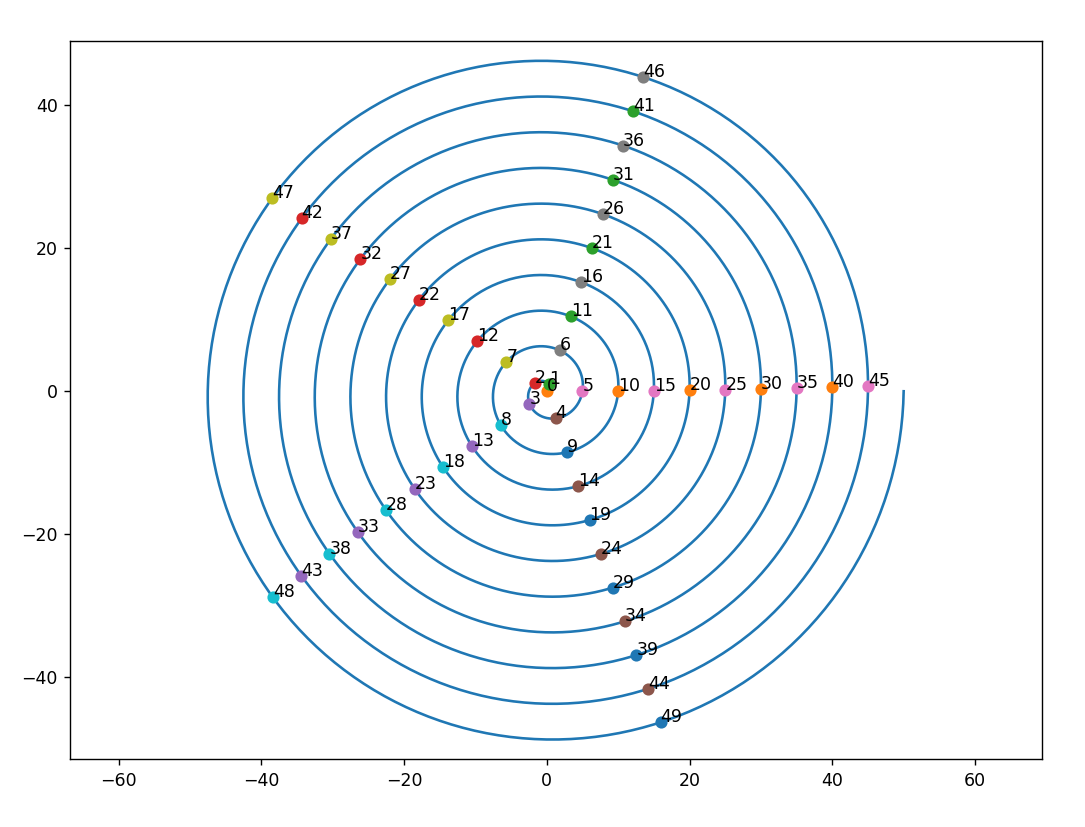
-
♥ juillet 2023 : une idée qui a fait son temps : on interpole la somme de somme de cos (qui s’annule pour les premiers) par une (smoothie !) cubique, on prend sa symétrique par rapport au milieu et on voit les points nuls communs qui sont les décomposants de Goldbach (729)
 
-
juillet 2023 : vieux souvenirs : programme d’éé d’une courbe presque aussi jolie que celle de Hilbert (Mandelbrot la dénomme Minkowski sausage, en l’honneur de son ami mort jeune) (728)
 
-
♥ juillet 2023 : graphique 1 : enfin ma surface bosselée avec les décompositions de Goldbach qui ’’tombent au sol’’ (z=0) en python, graphique 2 : Plaid Goldbach vu de dessus (on distingue en foncé 3+3, 3+5, 3+7), graphique 3 : les nombres premiers de 3 à 19 vus en coupe de profil de la surface bosselée et enfin, plaid 500 en python (727)
   
-
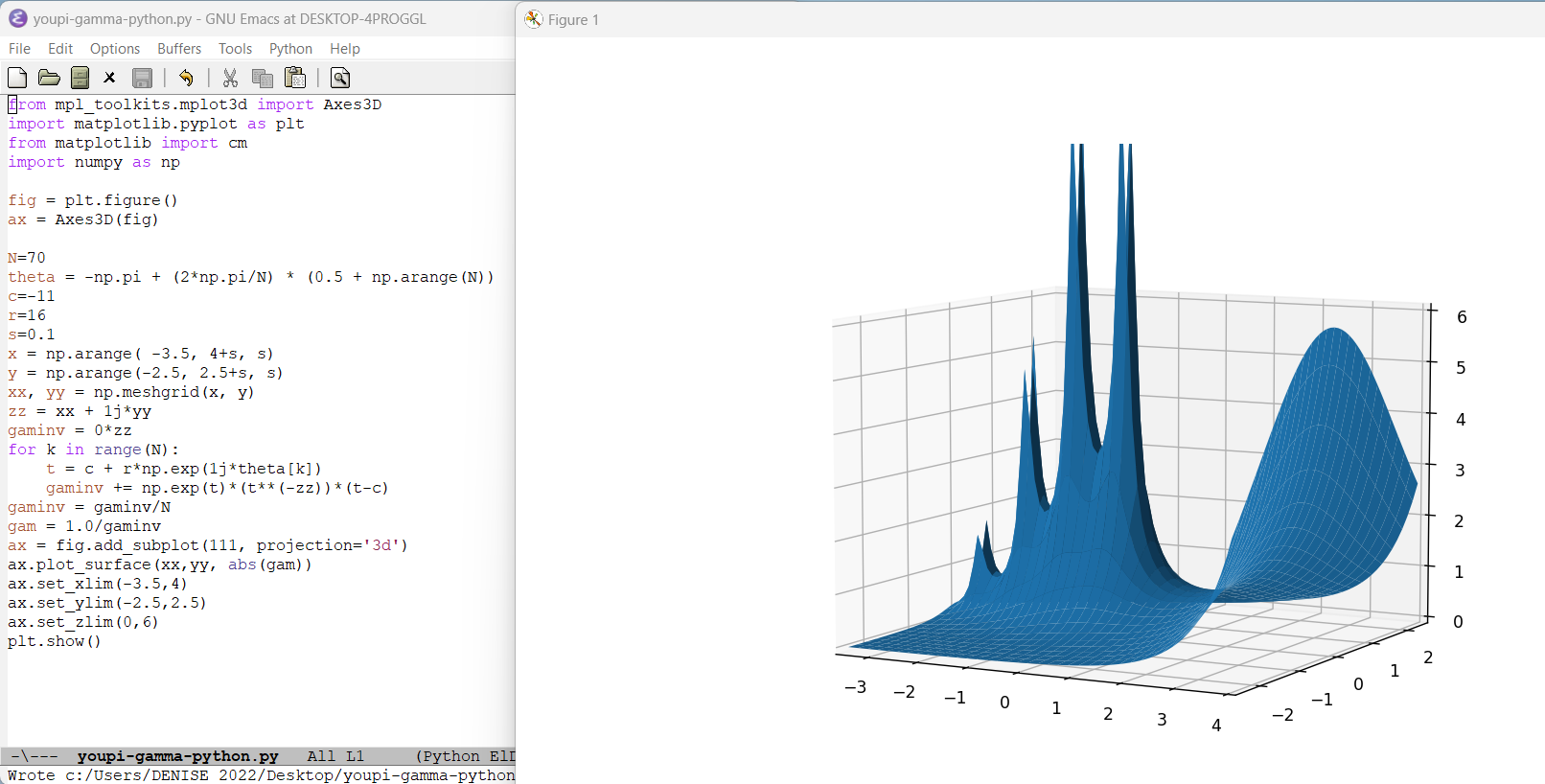
juillet 2023 : plot de Gamma en python et miroir du théorème de Wilson (726)
 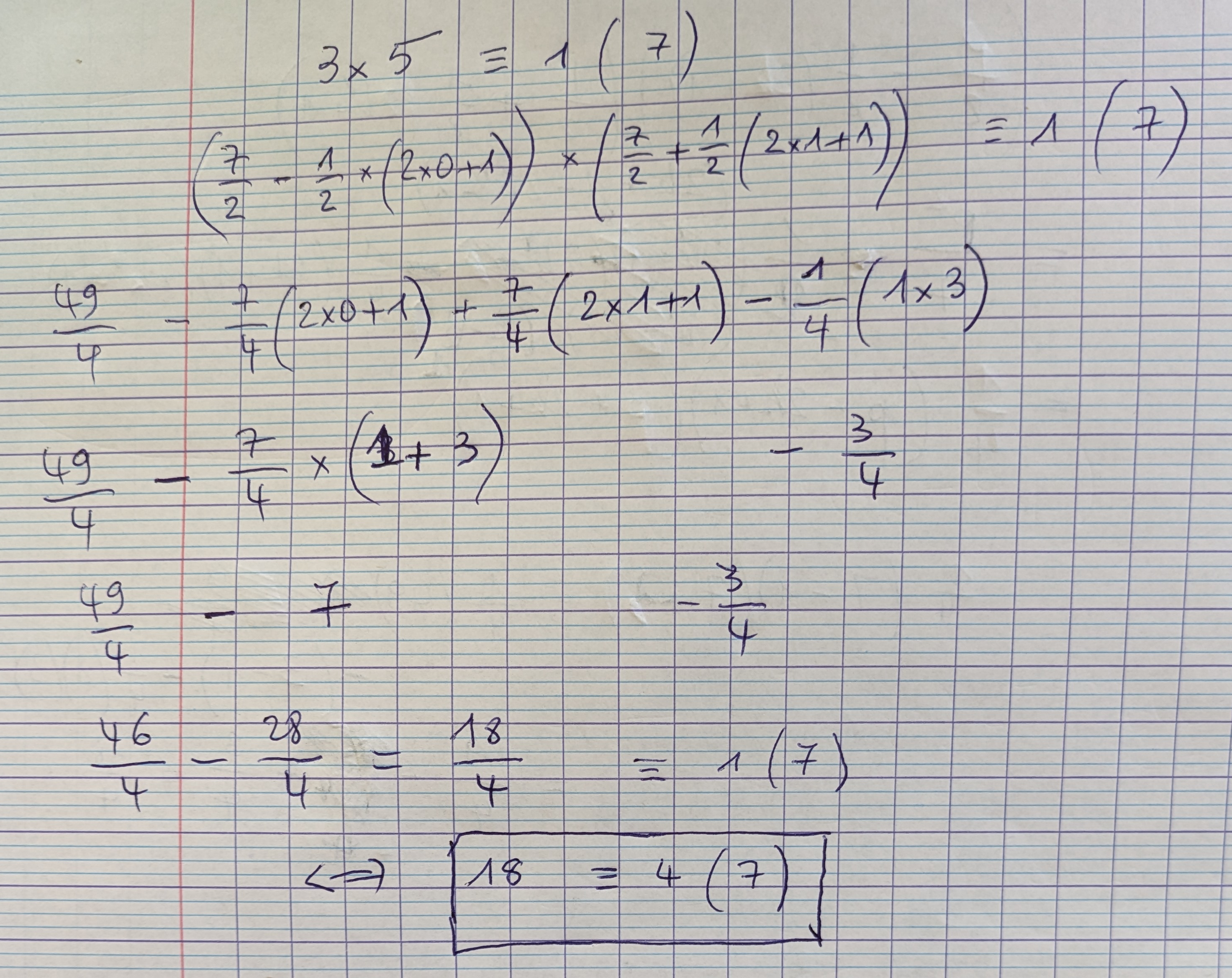
-
juillet 2023 : essayer de comprendre la théorie spectrale en programmant (725)

-
juin 2023 : indices concordants (724)

-
juin 2023 : les calculs d’Estelle Sonnenblick pour David Slepian
 
-
juin 2023 : essayer de programmer les fonctions prolate pour le spectre de la fonction zeta (723)

-
juin 2023 : une incompréhension au sujet des sommes quadratiques de Gauss
 voir forum voir forum 
-
30.5.2023 : Flèches (on n’a pas noté un trait de 1 à -1 pour les doubles de premiers (leur décomposition de Goldbach triviale) (722)

-
juin 2023 : explication du cercle qui est transformé en une droite (721)

-
juin 2023 : Retrouver la mémoire d’un retraité de Bourbaki
 Histoire de l’IHÉS par Louis Michel Histoire de l’IHÉS par Louis Michel  
-
31.5.2023 : Nombres premiers et valeurs propres (720)

-
25.5.2023 : Comment une valeur propre de matrice peut-elle permettre de distinguer les nombres premiers (719)
des nombres composés ? 
-
10.6.2023 : Traduction du mémoire d’Arthur Cayley sur la théorie des matrices
 
-
15.5.2023 : Graphe du plus petit décomposant de Goldbach des nombres pairs jusqu’à 107 (718)
    
-
8.5.2023 : Quoi de neuf ? (717)

-
1.5.2023 : Impression (716)

-
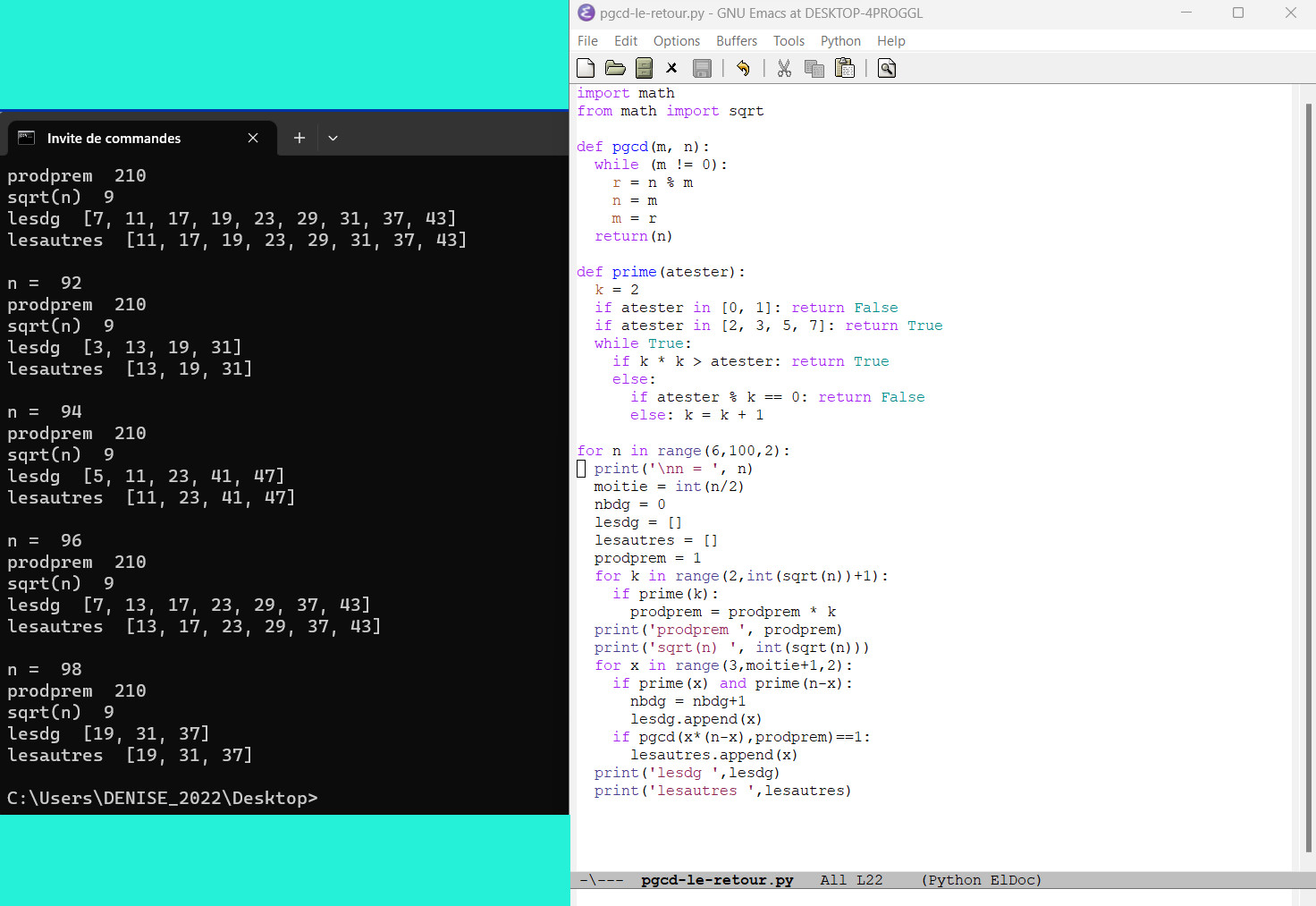
28.4.2023 ou pgcd, le retour : ce programme est rigolo : on prend les nombres tels que x(n-x) est premier au produit des nombres premiers inférieurs à √n, ça élimine les composés ou les nombres de complémentaires composés, et ça trouve donc les décomposants de Goldbach de n supérieurs à √n. (715)
-
20.4.2023 : petits premiers (714)

-
avril 2023 : retour aux matrices (713)

-
avril 2023 : tous pour un (712)

-
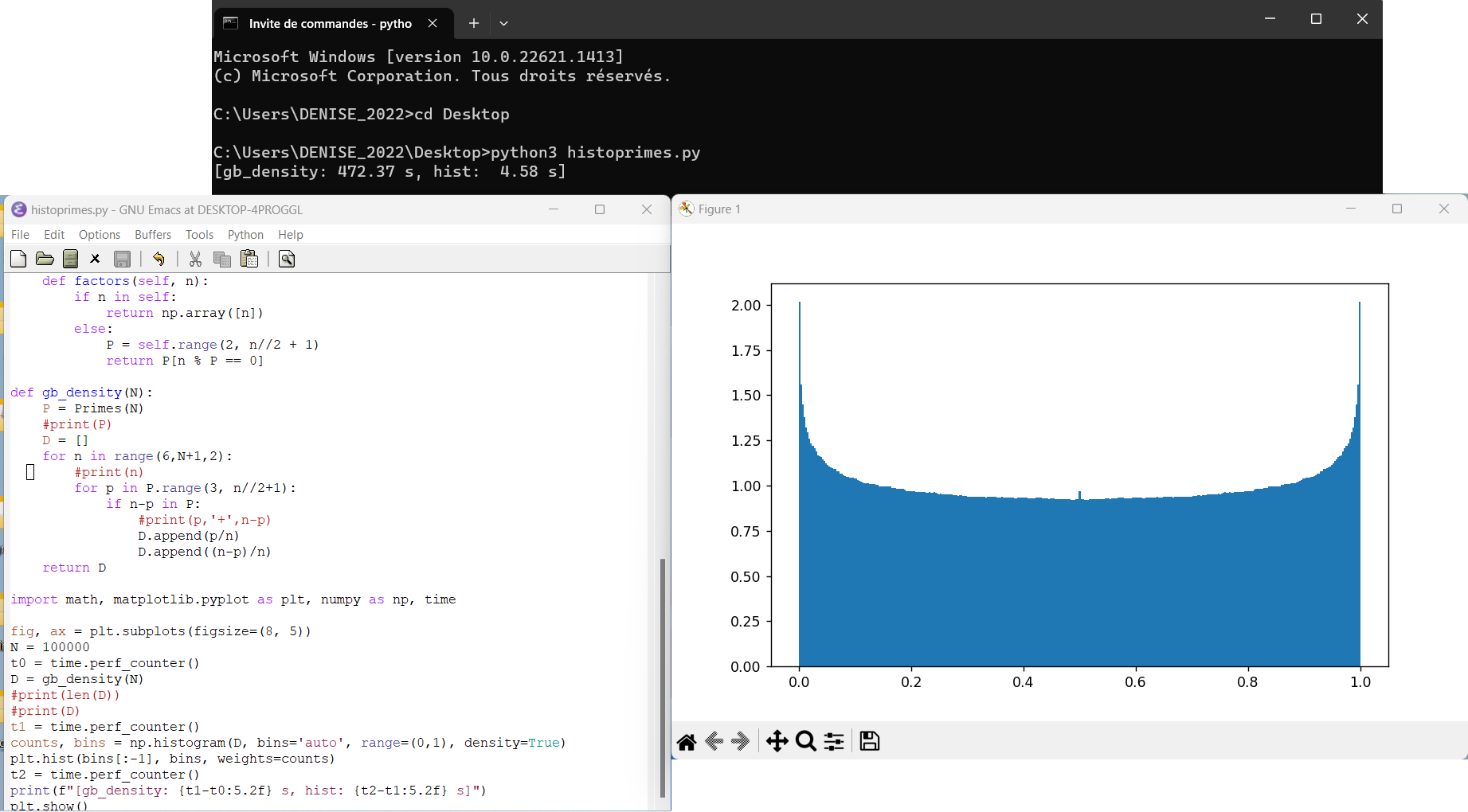
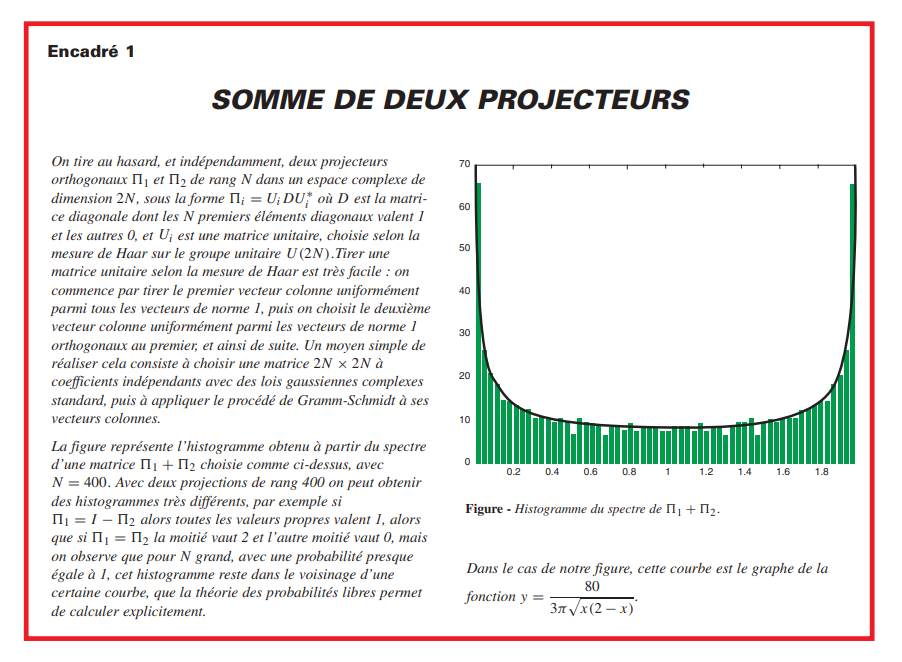
2.4.2023 : histogrammes des décomposants de Goldbach ramenés sur [0,1] (711)
-
25.3.2023 : Si tous étaient bien répartis... (710)

-
15.3.2023 : matrices de projections (709)

-
mars 2023 : bla-bla car... (708)

-
8.3.2023 : polytope pour décomposants de Goldbach (707)

-
26.2.2023 : gourmandise (706)

-
février 2023 : géométrie des nombres et décomposants de Goldbach (705)

-
9.2.2023 : découverte d’une loi tout extraordinaire (704)

-
février 2023 : Traduction des interventions dans le film Maryam Mirzakhani : Les secrets de la Surface
 
-
janvier 2023 : Ici, j’ai mis les nombres premiers p tels que (p-1)/2 est premier aussi (ce sont les correspondants des nombres premiers de Sophie Germain (un nombre premier p est de Sophie Germain si 2p+1 est premier aussi)) (703)

-
février 2023 : Identités de Liouville, parité, récurrence d’Euler pour la somme des diviseurs (702)

-
3.1.2023 : Logique classique et logique intuitionniste sont asymptotiquement identiques
 propriétés statistiques des types simples (où étonnamment, le nombre d’or intervient) (700) propriétés statistiques des types simples (où étonnamment, le nombre d’or intervient) (700)  
-
♥ janvier 2023 : Conjecture de Goldbach et logique propositionnelle (propositions à une variable) (699)
 (en) (en) 
-
25.12.2022 : Comète de Goldbach et Golden ratio (nombre d’or) (698)

-
24.11.2022 :

-
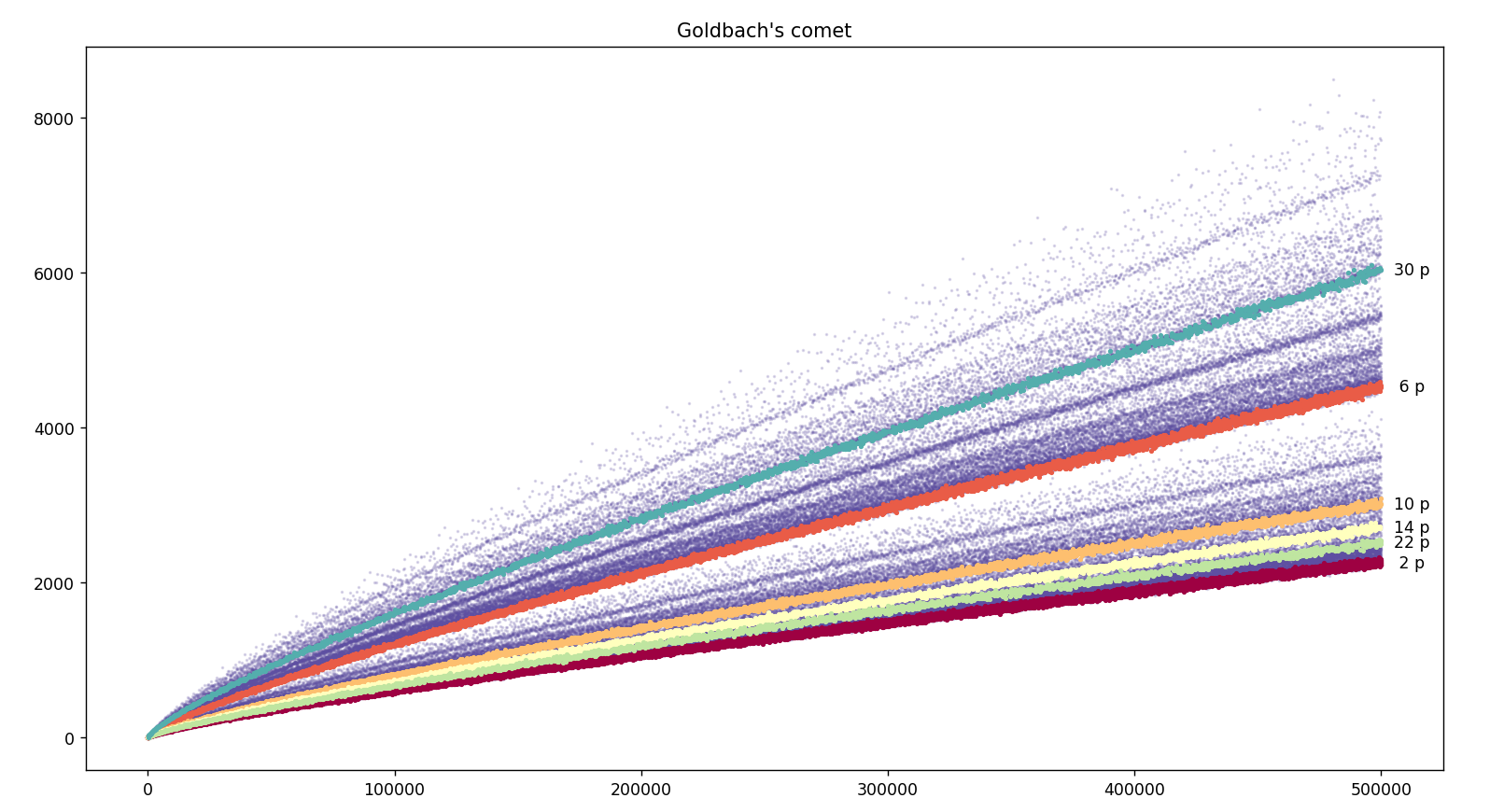
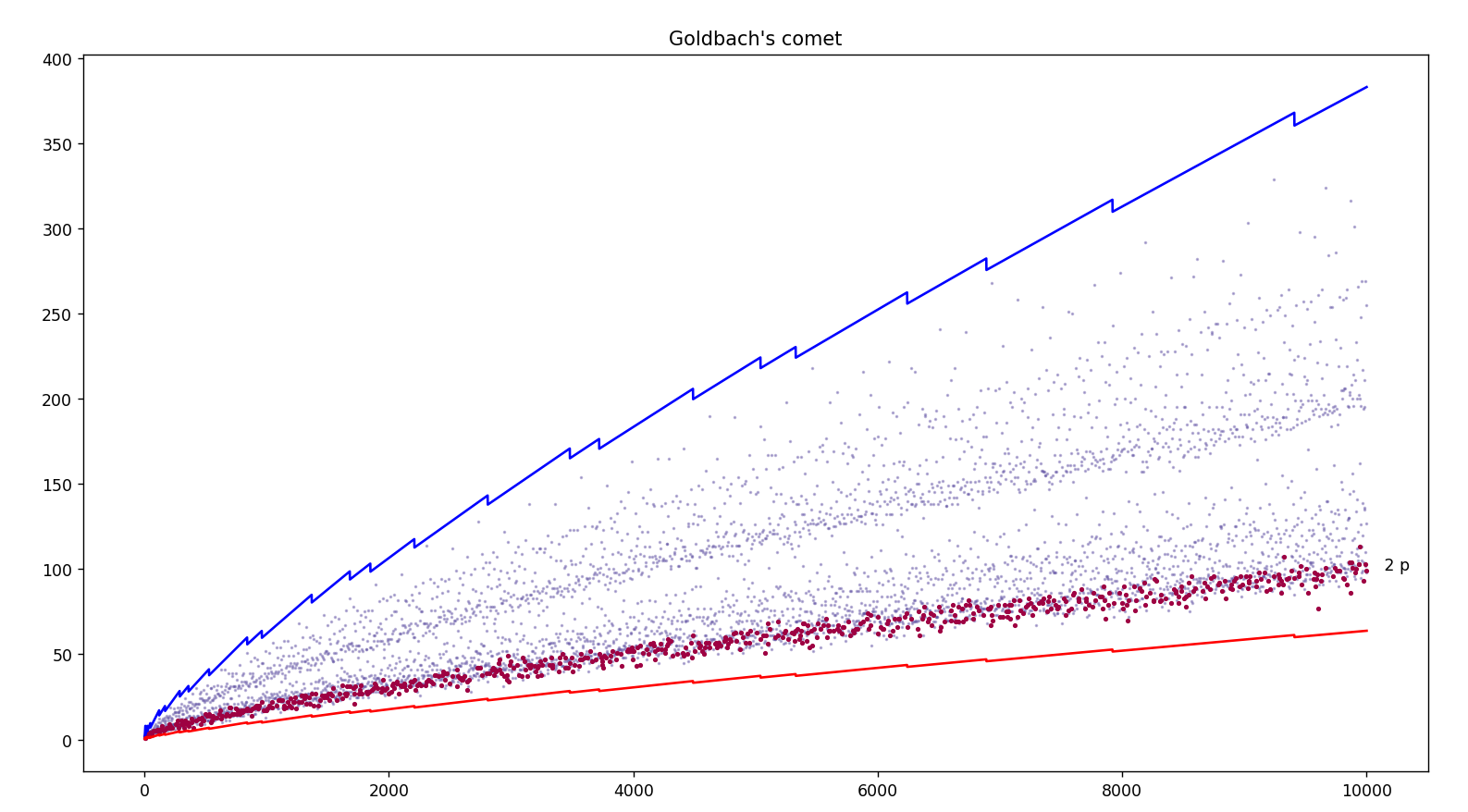
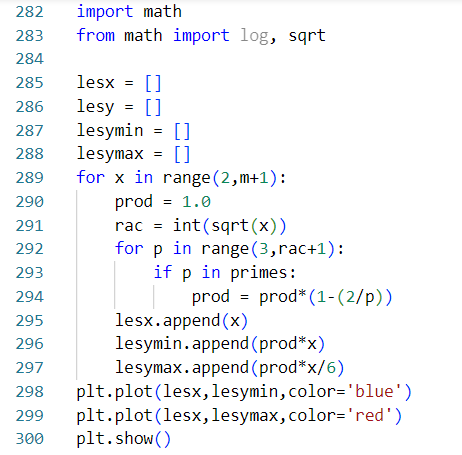
♥ 19.11.2022 : que le nombre d’or φ soit caché dans la comète des nombres de décompositions de Goldbach, ça devrait couler sous le sens ! (Les programmes sont la légende des courbes : la rouge (Prod(1-2/p).x/6, avec p premier < √x), la jaune (2φ.x/(5.log(x).log(x))) et la rose (φx/(√5.log(x).log(x))) semblent minorer la comète, la bleue semble la majorer (Prod(1-2/p).x, p premier < √x), et la verte φ.x/(log(x).log(x)) semble tomber pile au milieu des nombres de décompositions des pairs de la forme 6p, avec p premier).

  
-
13.11.2022 : on visualise dans la comète (programmes en python d’une idée de décembre 2010) que les nombres de décompositions de Goldbach sont partiellement ordonnés selon la relation de divisibilité (696)
-
octobre 2022 : programme python pour le calcul de π(x) par les sommes d’inverses de cumul de valuations p-adiques (695)
 fourvoiement complet : j’ajoute 1 sur les premiers et 0 sur les autres en prenant le floor d’un nombre entre 0 et 1, dur ! fourvoiement complet : j’ajoute 1 sur les premiers et 0 sur les autres en prenant le floor d’un nombre entre 0 et 1, dur !
-
octobre 2022 : représentations de fonctions de même allure (reprise d’un graphique de février 2006) (694)
       Toutes les images de ces fonctions plaisantes Toutes les images de ces fonctions plaisantes 
-
8.10.2022 : une fonction alignant les images des nombres premiers (693)

-
2.10.2022 : une fonction alignant les images des nombres premiers (692)

-
12.8.2022 : probabilité (691)
 (en) (en) 
-
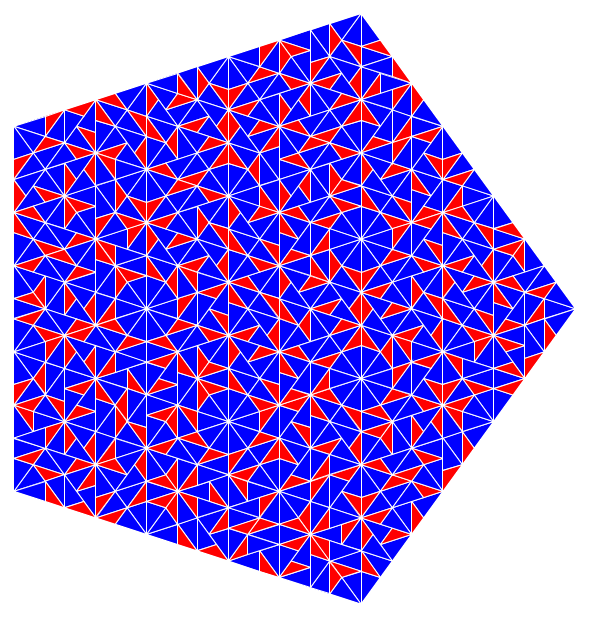
octobre 2022 : transcription (en 3 parties de 20 minutes chacune) de la vidéo de Penrose sur les symétries interdites
   traductions en français par outils Google traductions en français par outils Google    Je reprends les traductions fournies par l’IA Je reprends les traductions fournies par l’IA    Illustrations du livre Harmonices mundi de Johannes Kepler Illustrations du livre Harmonices mundi de Johannes Kepler  Traduction d’un article sur les pavages d’Ammann-Beenker Traduction d’un article sur les pavages d’Ammann-Beenker    





-
post-it : 3 anciennes notes regroupées sur sommes alternées de cosinus (689)
  
-
Septembre 2022 : traduction d’un article fondateur d’Alonzo Church traitant de théorie élémentaire des nombres


-
Juillet 2022 : moins deux (690)
 article de Rosser et Schoenfeld en référence article de Rosser et Schoenfeld en référence 
-
Juillet 2022 : continuer d’essayer de comprendre l’équation de Chazy (688)
 explication de Jacques (Chemla) pour le lien entre l’équation de Chazy et la somme des diviseurs d’un nombre explication de Jacques (Chemla) pour le lien entre l’équation de Chazy et la somme des diviseurs d’un nombre  traduction d’un article de Clarkson et Olver traduction d’un article de Clarkson et Olver 
-
27.7.2022 : densité (687)

-
juillet 2022 : se rappeler de la note sur les mots apériodiques de 2017 (compositions des nombres "à la Knuth" et mots apériodiques pour les nombres premiers) (686)

-
23.7.2022 : Calcul complètement raté (682)

-
22.7.2022 : polynômes (685)

-
16.7.2022 : deux en moins (684)

-
25.5.2022 : remplacer les triangles par des carrés (de chocolat) mais comment faire pour qu’il n’y ait pas de cycles à sommets sur plusieurs lignes ? (681)
-
15.5.2022 : énoncé de CG en logique du premier ordre (680)

-
11.5.2022 : Petits triangles (679)

-
14.4.2022 : Nombres p-adiquement éloignés (merci à Bertrand Hauchecorne) (678)

-
8.3.2022 : Racines de certaines équations modulaires (677)

-
23.2.2022 : Unités racines de certaines équations (676)
 Décès de Gauss le 23.2.1855 Décès de Gauss le 23.2.1855 
-
19.2.2022 : être sûr de pouvoir les décomposer tous ou nombre d’automorphismes intérieurs à certains nombres de points fixes (674)

-
19.2.2022 : Programmation de la démonstration du théorème de Morley par Alain Connes (673)

-
24.1.2022 : Faire des sommes (669)

-
20.1.2022 : Unités vérifiant certaines équations dans lesquelles intervient la fonction φ d’Euler (675)
 équations plutôt qu’intersections ensemblistes équations plutôt qu’intersections ensemblistes 
-
26.12.2021 : Behind the scene (672)

-
19.12.2021 : Descente infinie (671)

-
19.12.2021 : Traduction d’un extrait du TAOCP au sujet de l’algorithme d’Euclide étendu
 
-
18.12.2021 : Algorithme d’Euclide étendu pour décomposants de Goldbach (670)

-
10.12.2021 : Remarques d’Henri Cartan
 
-
10.12.2021 : Grilles, le retour (668)

-
1.12.2021 : Cribles de Grothendieck pour Goldbach (667)

-
29.11.2021 : 3 ou 5 égal 7 (666)

-
17.11.2021 : Traduction des sous-titres d’une vidéo d’Avi Wigderson (prix Abel 2021 avec László Lovász
 ) sur les preuves à divulgation nulle ) sur les preuves à divulgation nulle  Traduction de l’article contenant le théorème de Cook Traduction de l’article contenant le théorème de Cook  Traduction de l’article contenant le théorème de Levin Traduction de l’article contenant le théorème de Levin  Interview pour l’EMS Interview pour l’EMS  
-
10.11.2021 : Travailler modulo 1 (664)
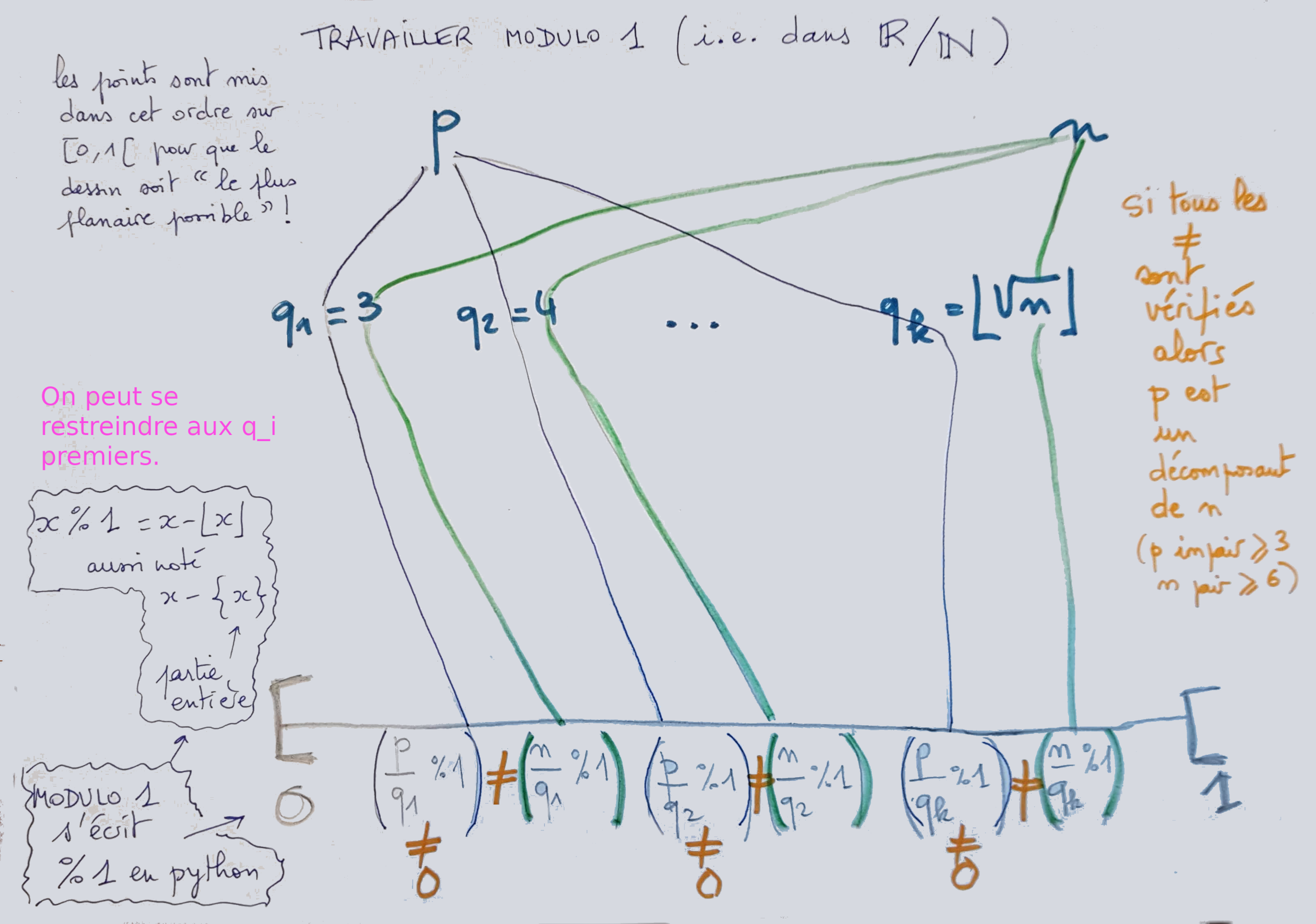
-
2.11.2021 : formule 2.6 du Rosser et Schoenfeld (665)
 30.1.2022 : par programme plutôt que par formule, la minoration du nombre de décomposants de Goldbach par la somme des (p-2)/p pour p premier compris entre 3 et √n semble toujours vraie à partir de n=1414 30.1.2022 : par programme plutôt que par formule, la minoration du nombre de décomposants de Goldbach par la somme des (p-2)/p pour p premier compris entre 3 et √n semble toujours vraie à partir de n=1414 
-
19.10.2021 : Transcription et traduction d’un cours d’Alain Connes The Riemann flow and the zeros of zeta (1998, SUNY, Stony Brook, New York)
   
-
12.10.2021 : garder trace des dernières expériences de programmation (663)

-
4.10.2021 : Turing et sa machine à prévoir les marées
 6.10.2021 : traduction d’un article de Booker et Platt : Méthode de Turing pour la fonction zeta de Selberg 6.10.2021 : traduction d’un article de Booker et Platt : Méthode de Turing pour la fonction zeta de Selberg  
-
3.10.2021 : Produits de sinus mieux dessinés en python pour voir les décomposants de Goldbach de 98 (662)
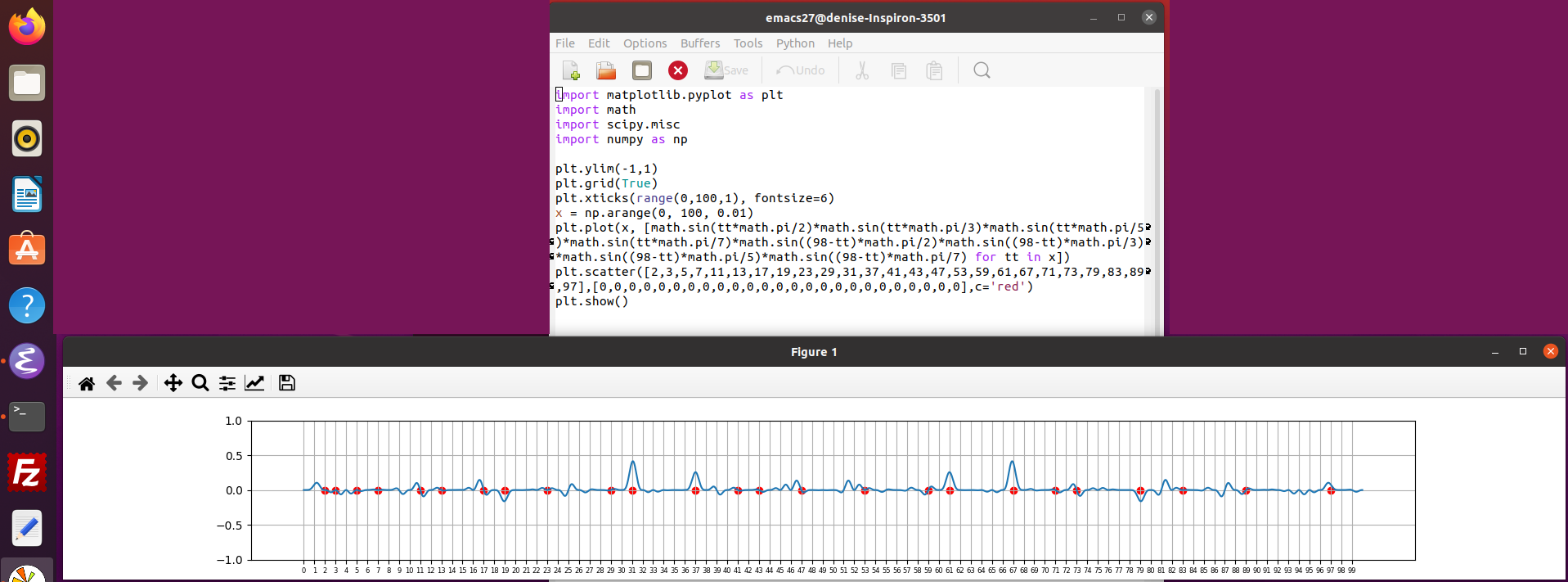 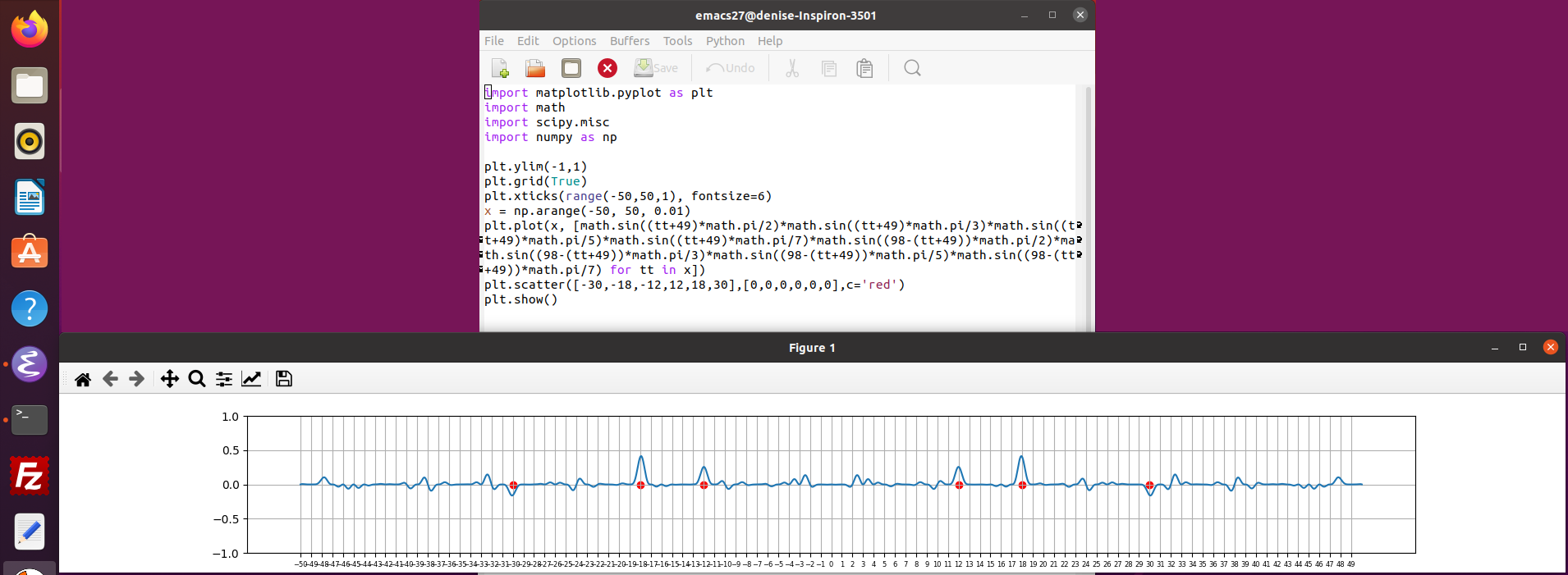 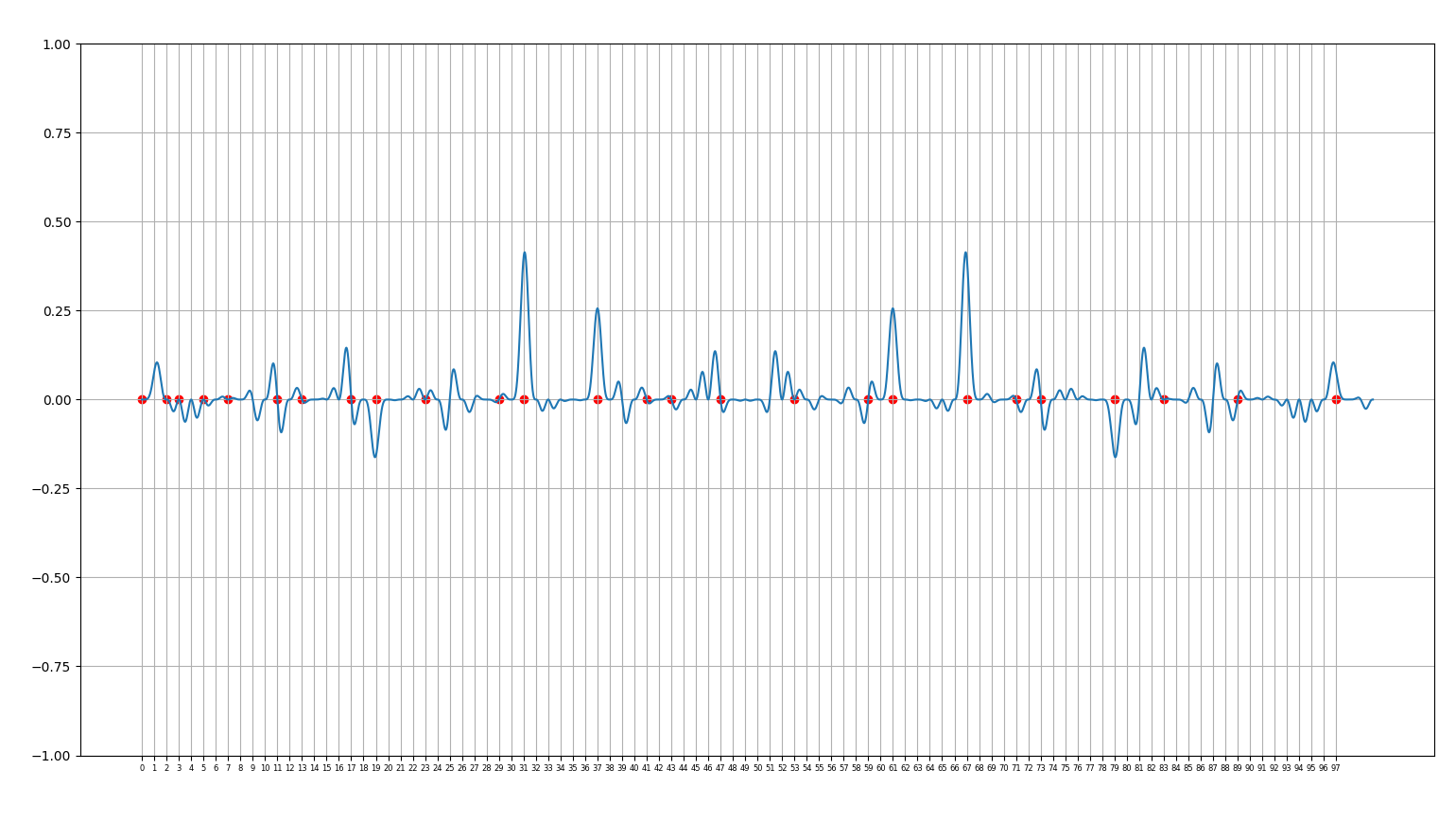
une fonction ancienne utilisant les zéros de zeta qui "pique" les premiers
-
2.10.2021 : Interview de Knuth pour le tout nouveau journal ECA

-
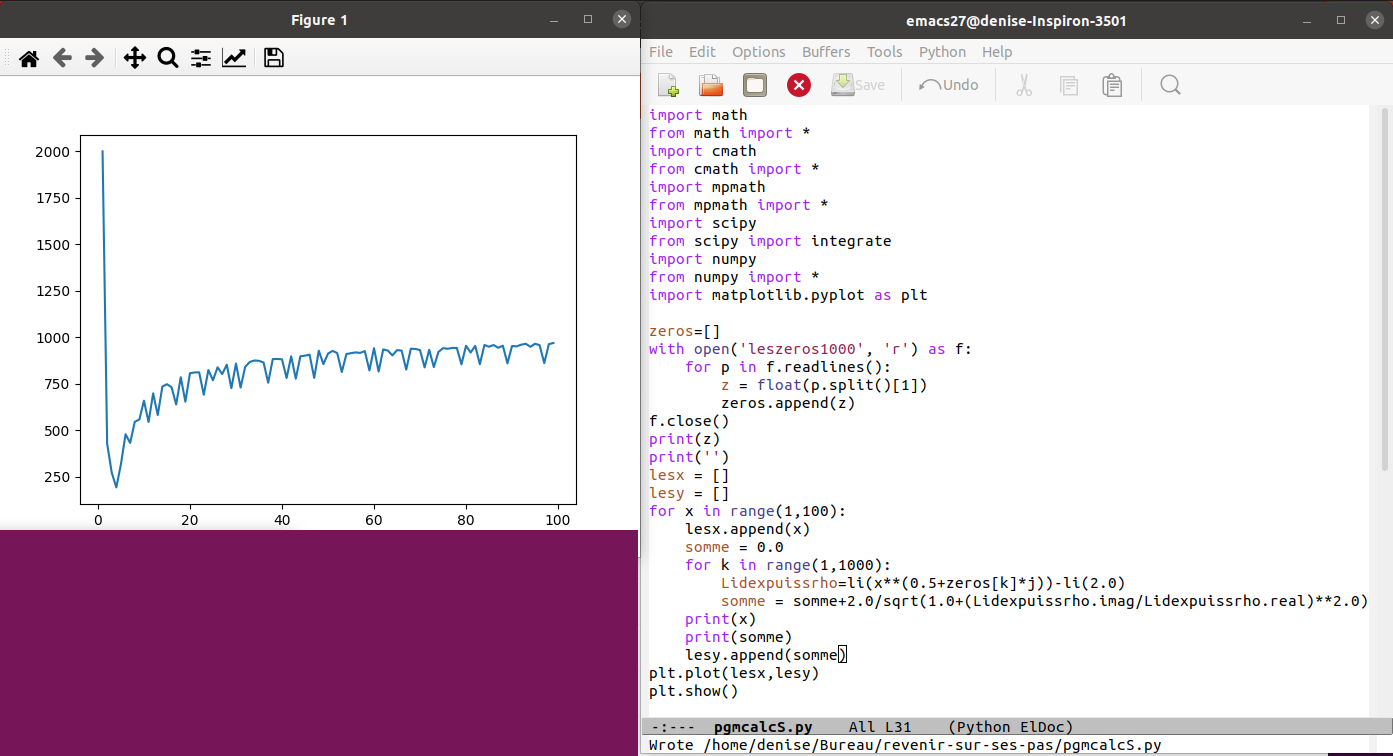
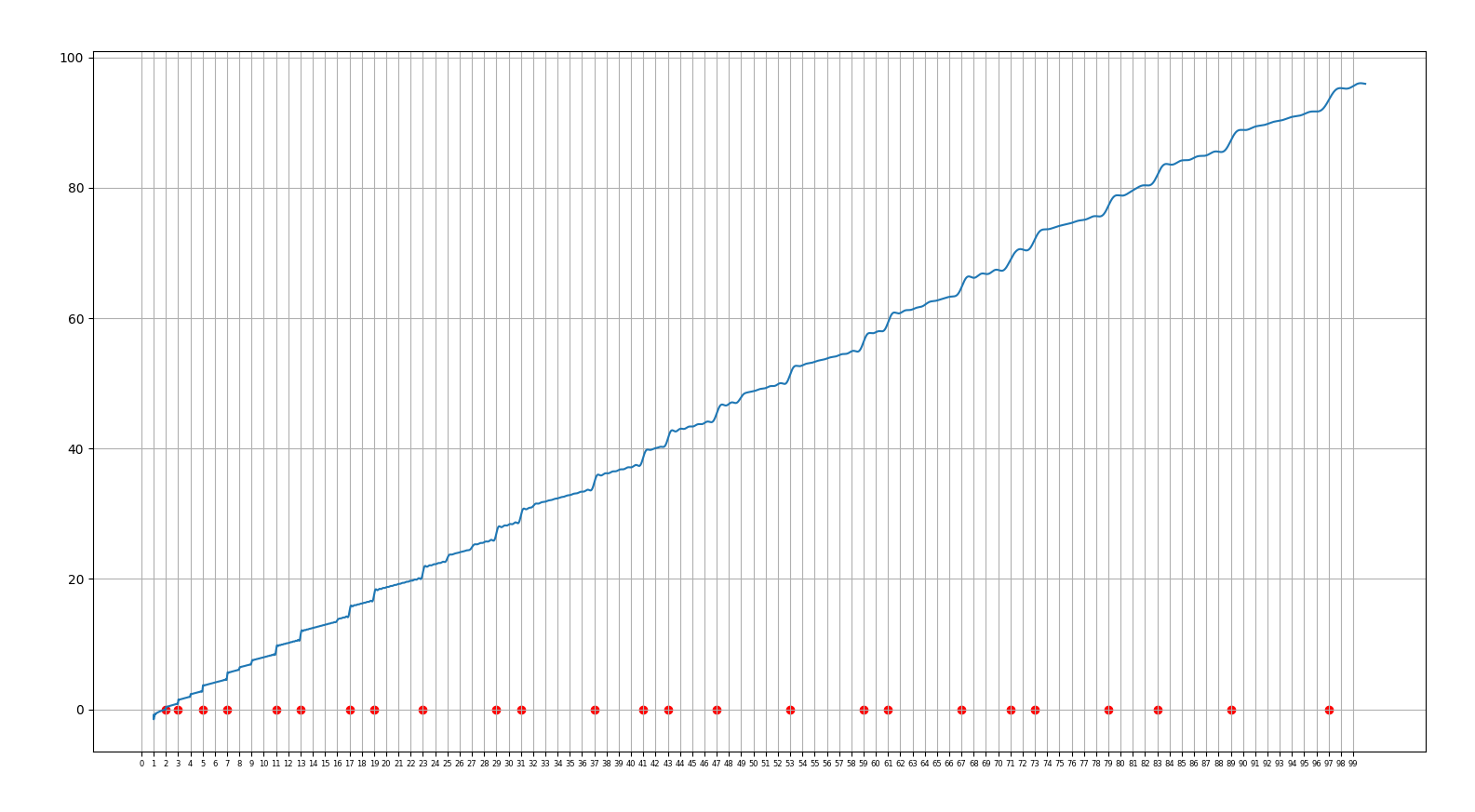
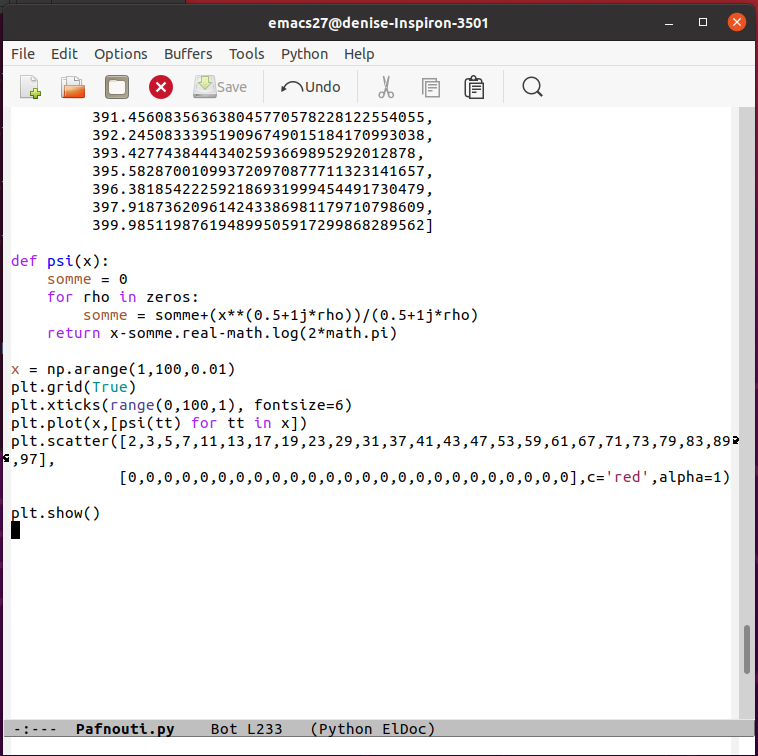
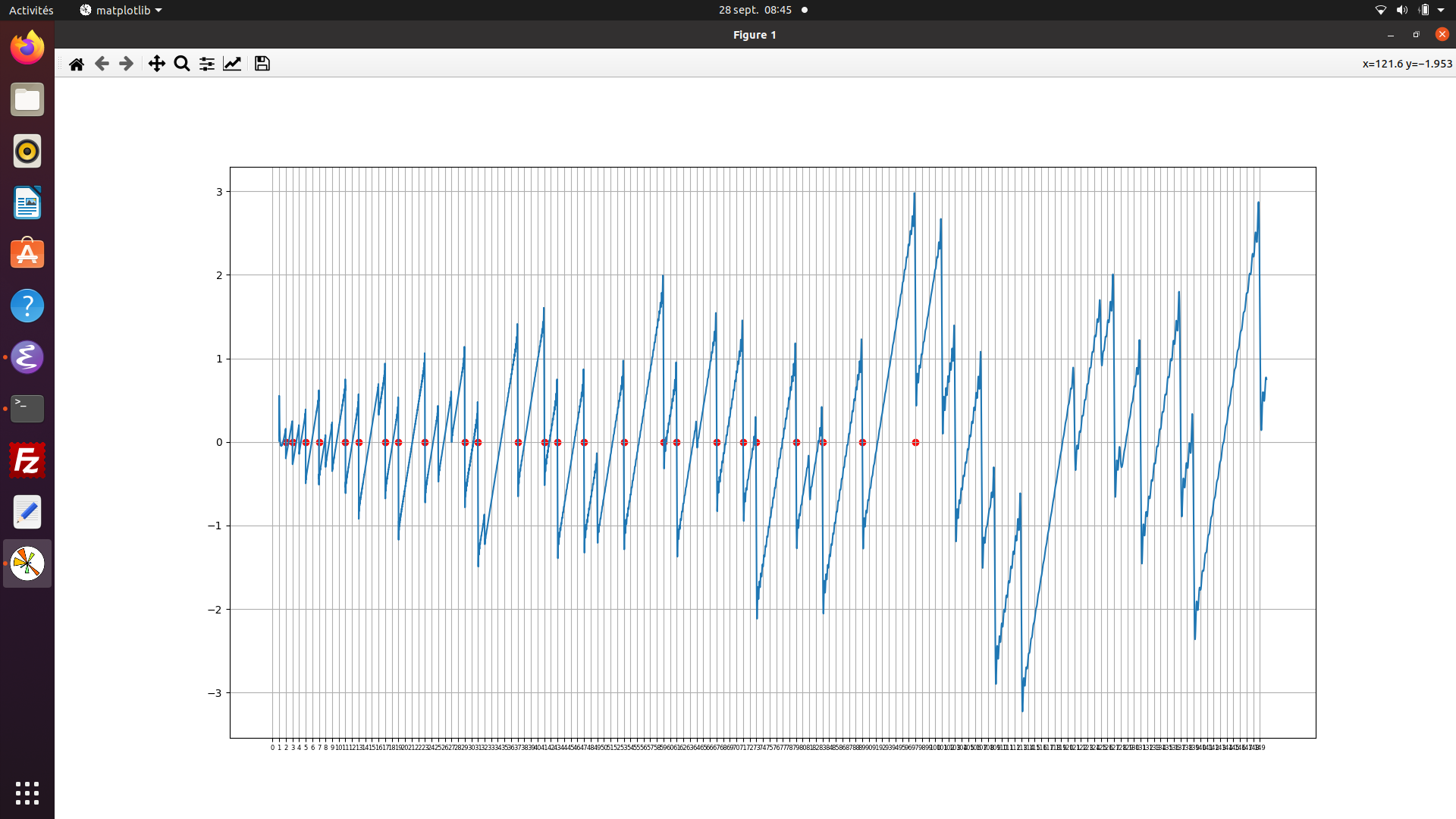
27.9.2021 : Fonction ψ de Chebyshev et Théorème de Von Mangoldt fournis par Matiyasevich lors d’une conférence à Stanford (slides consultables ici (661)
 ) )   
-
27.9.2021 : La seconde fonction fournie par Mazur dans la conférence (660)
 (mn 32 et suiv.) qui permet de trouver les nombres premiers à partir des zéros de zeta (utilisation des 100 premiers zéros puis des 1000 premiers zéros) (mn 32 et suiv.) qui permet de trouver les nombres premiers à partir des zéros de zeta (utilisation des 100 premiers zéros puis des 1000 premiers zéros) 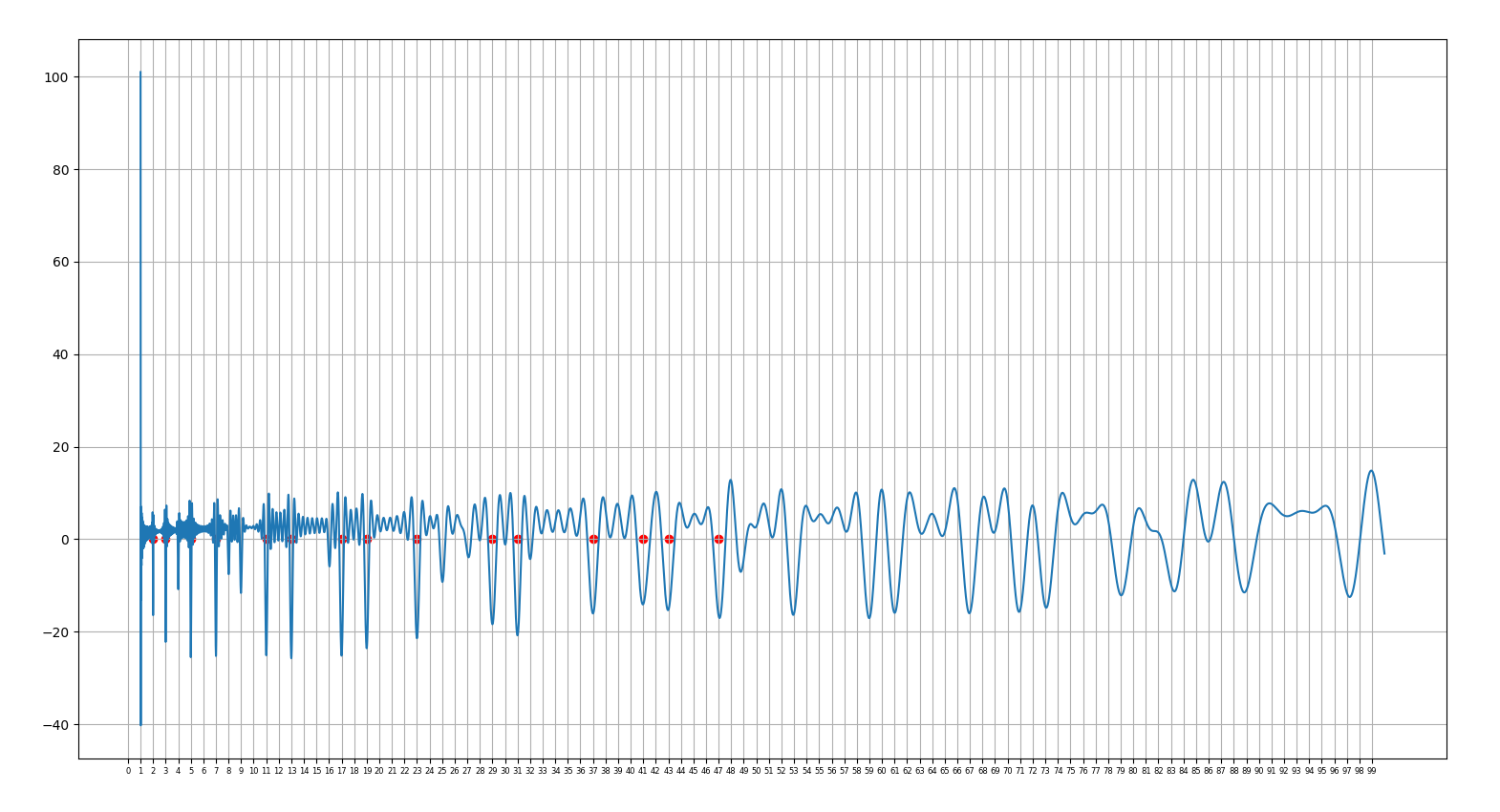 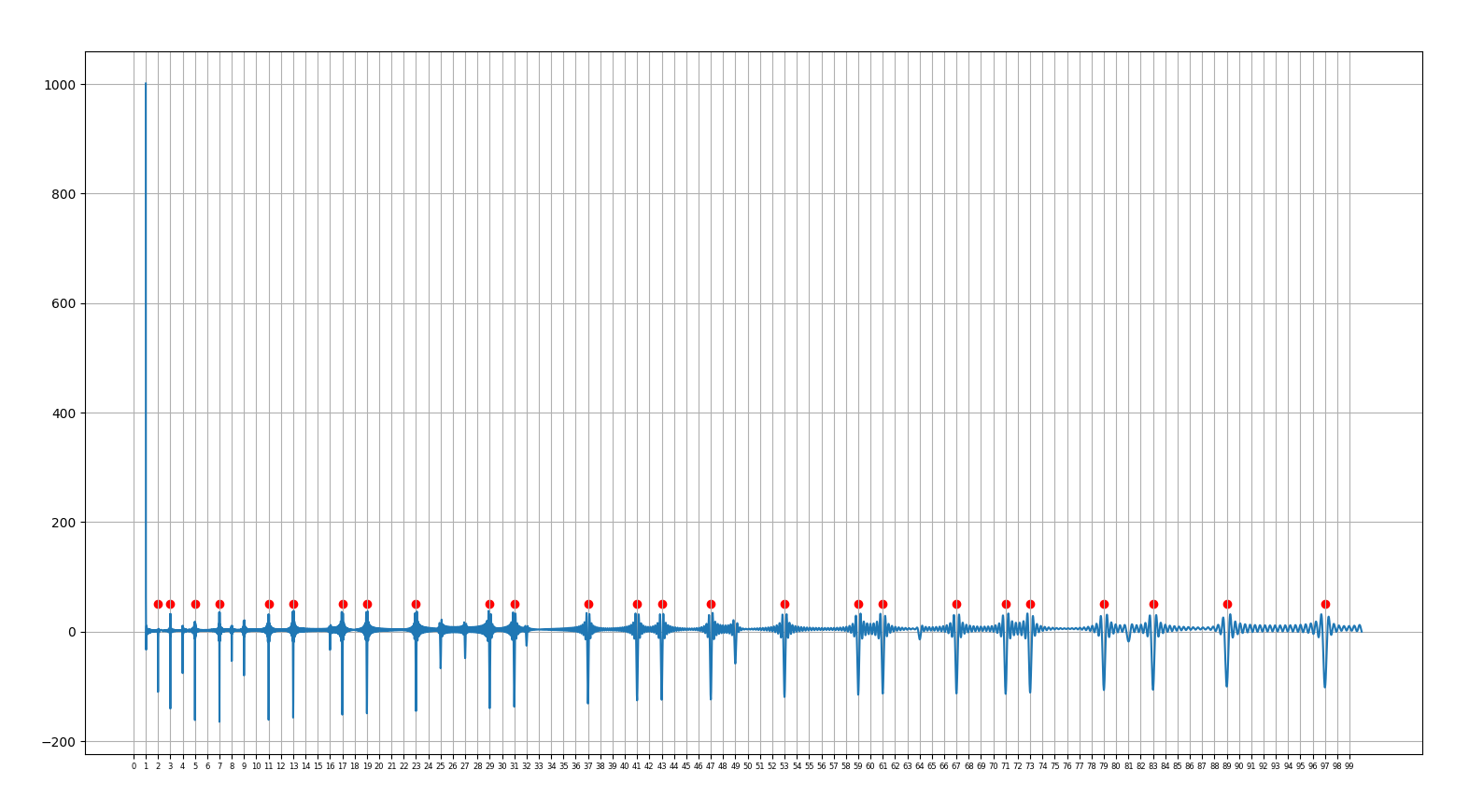 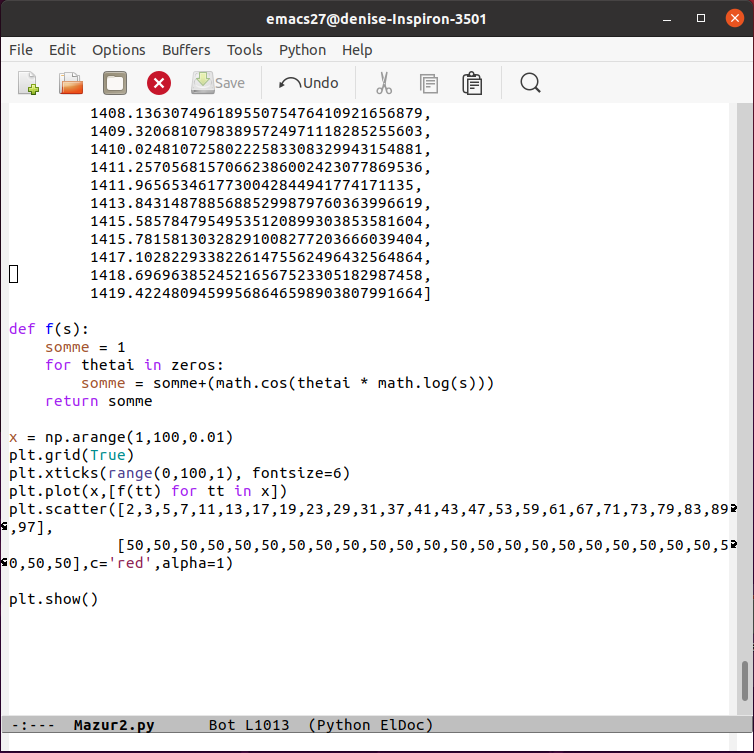 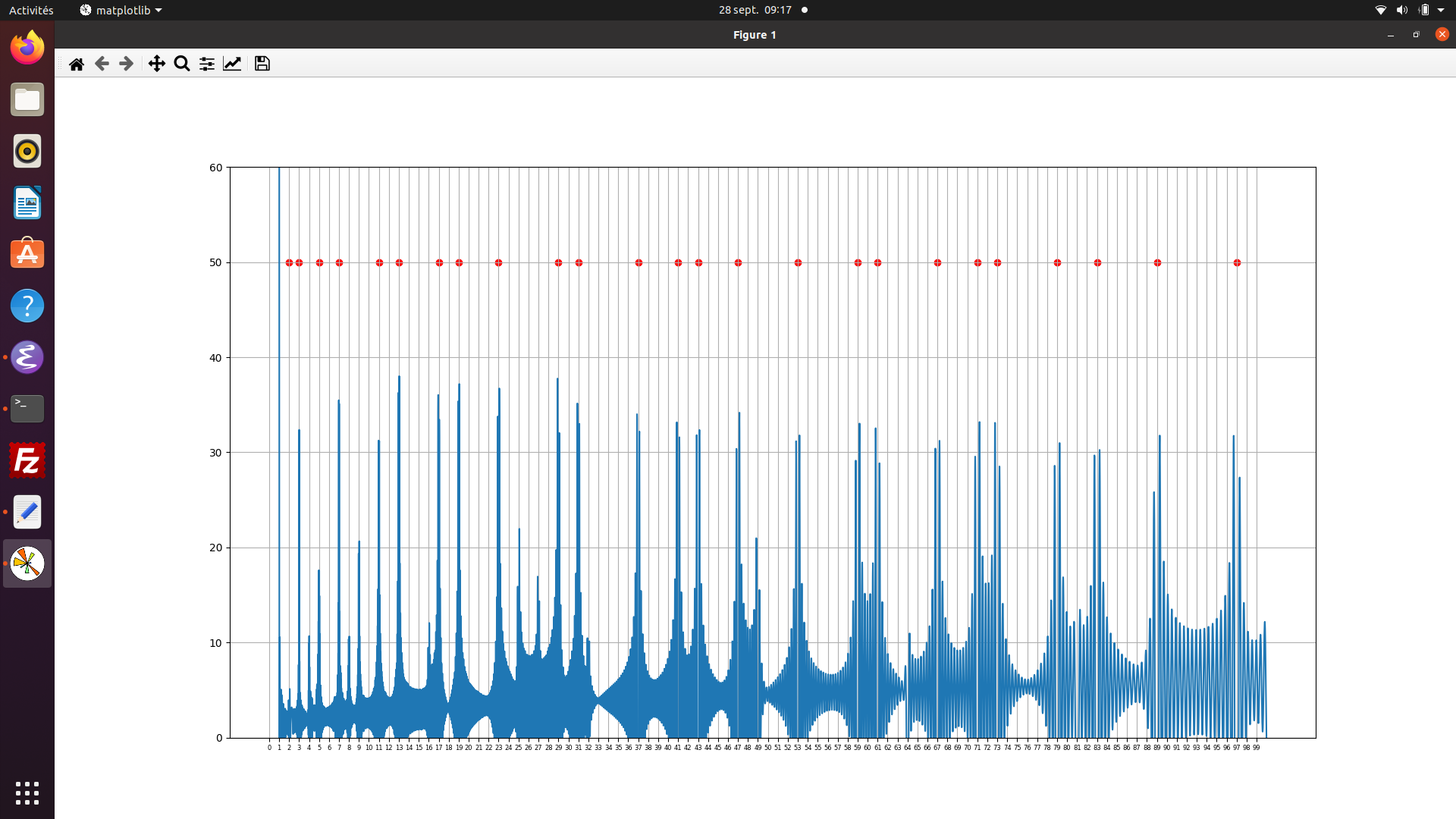
-
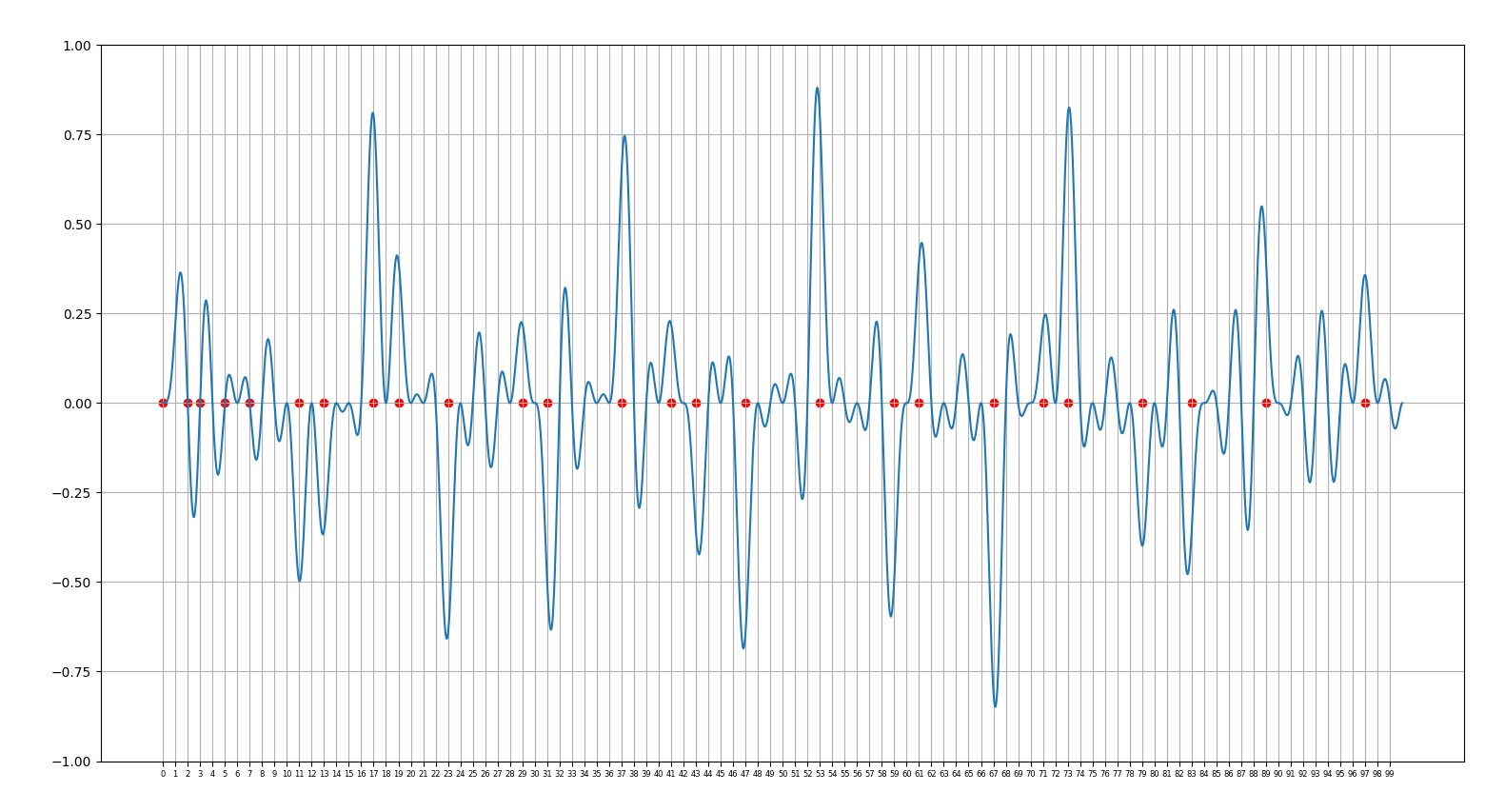
24.9.2021 : La fonction fournie par Mazur dans la conférence (659)
 (mn 32 et suiv.) qui permet de visualiser les zéros de zeta dans certains de ses pics particuliers (mn 32 et suiv.) qui permet de visualiser les zéros de zeta dans certains de ses pics particuliers  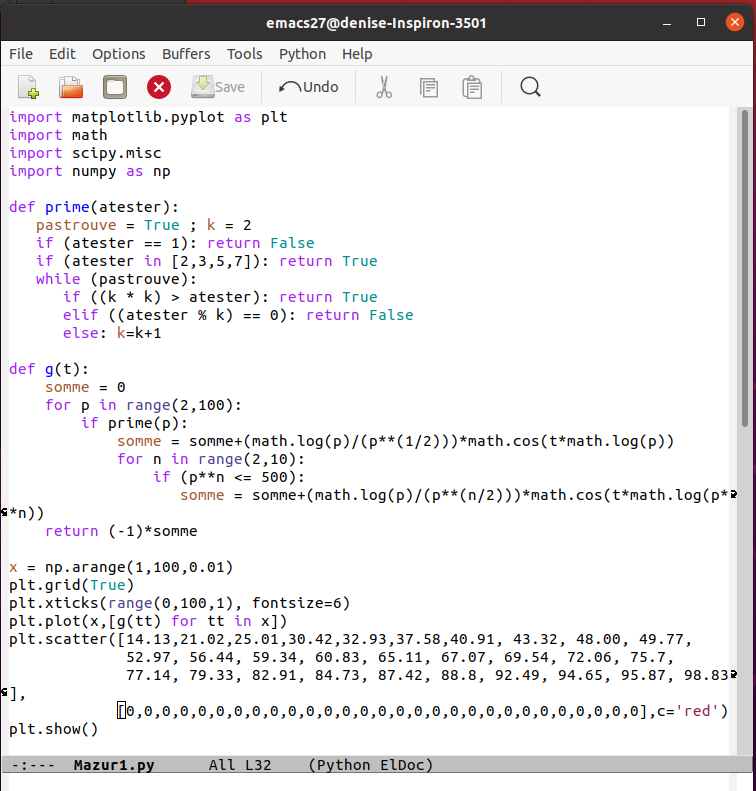
-
22.9.2021 : Complètement chaos, OK ?! (658)
 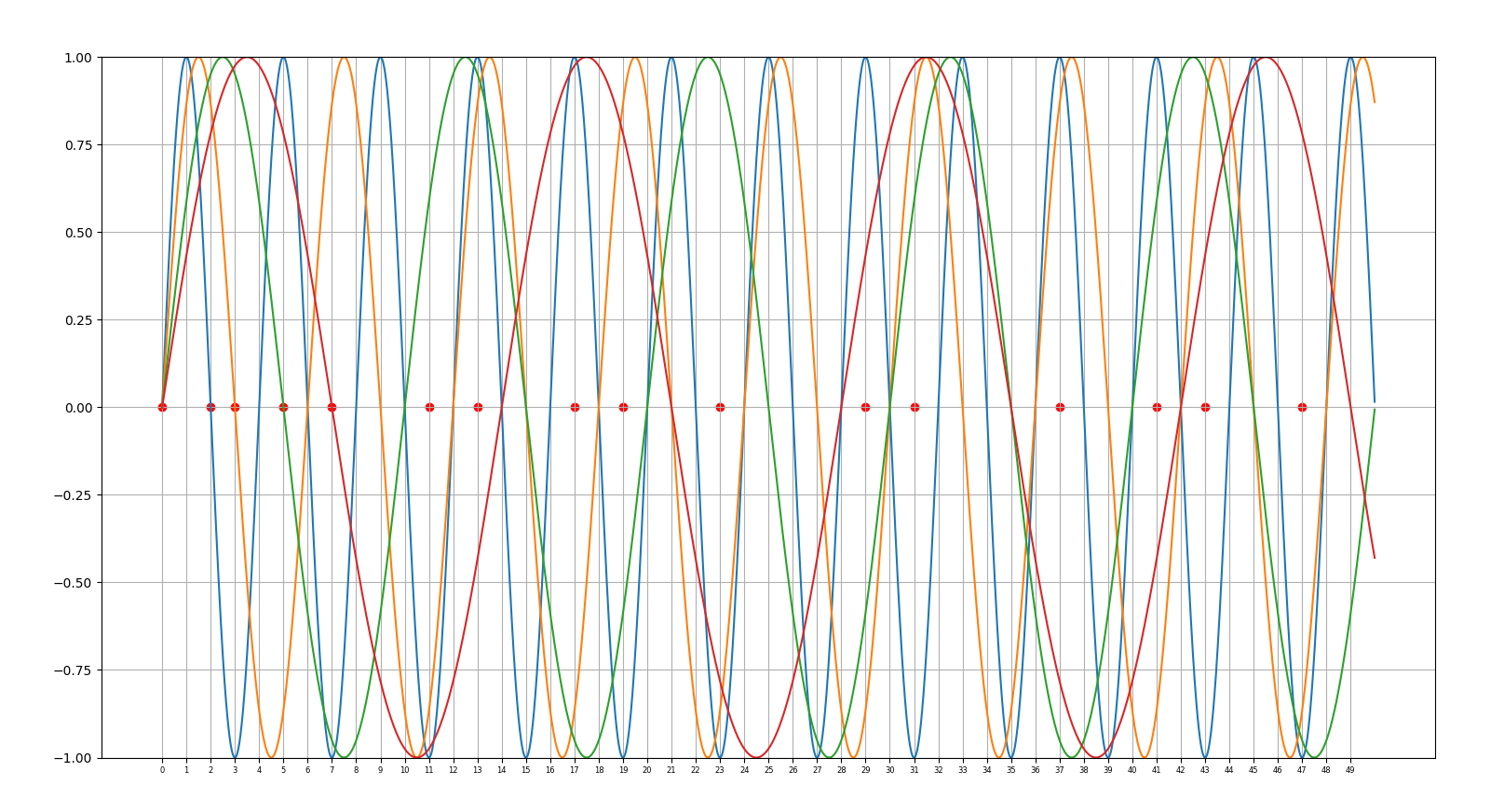 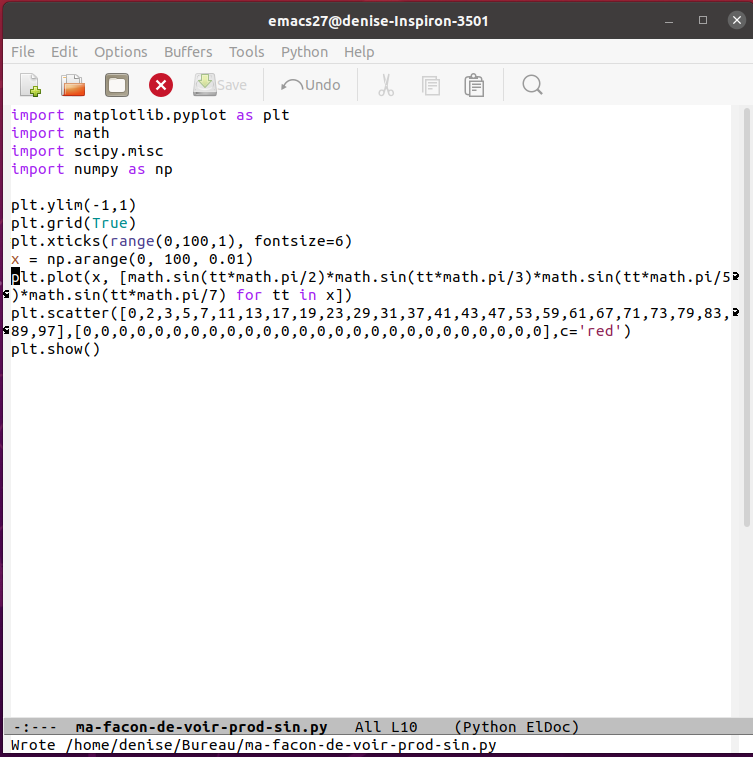
J’ai retrouvé "mon" produit de sinus dans la première page de cet article de Redheffer de 1951 
-
Oliver Heaviside et le calcul opérationnel
 et liens vers deux textes de Pierre Humbert et Serge Colombo : Le calcul symbolique et ses applications à la physique mathématique (1947, 1965) et liens vers deux textes de Pierre Humbert et Serge Colombo : Le calcul symbolique et ses applications à la physique mathématique (1947, 1965)  
-
5.9.2021 : quelle coïncidence ! Les initiales de son nom sont mes initiales initiales (Vella Denise, Paule) et van der Pol m’aura appris à calculer les zéros de zeta (en python, plutôt qu’avec des rayons de lumière traversant une sorte de scie circulaire lancée à toute vitesse)... Et sans Jacques, je n’aurais pas réussi (voir l’article de référence traduit en août un peu plus bas). (657)
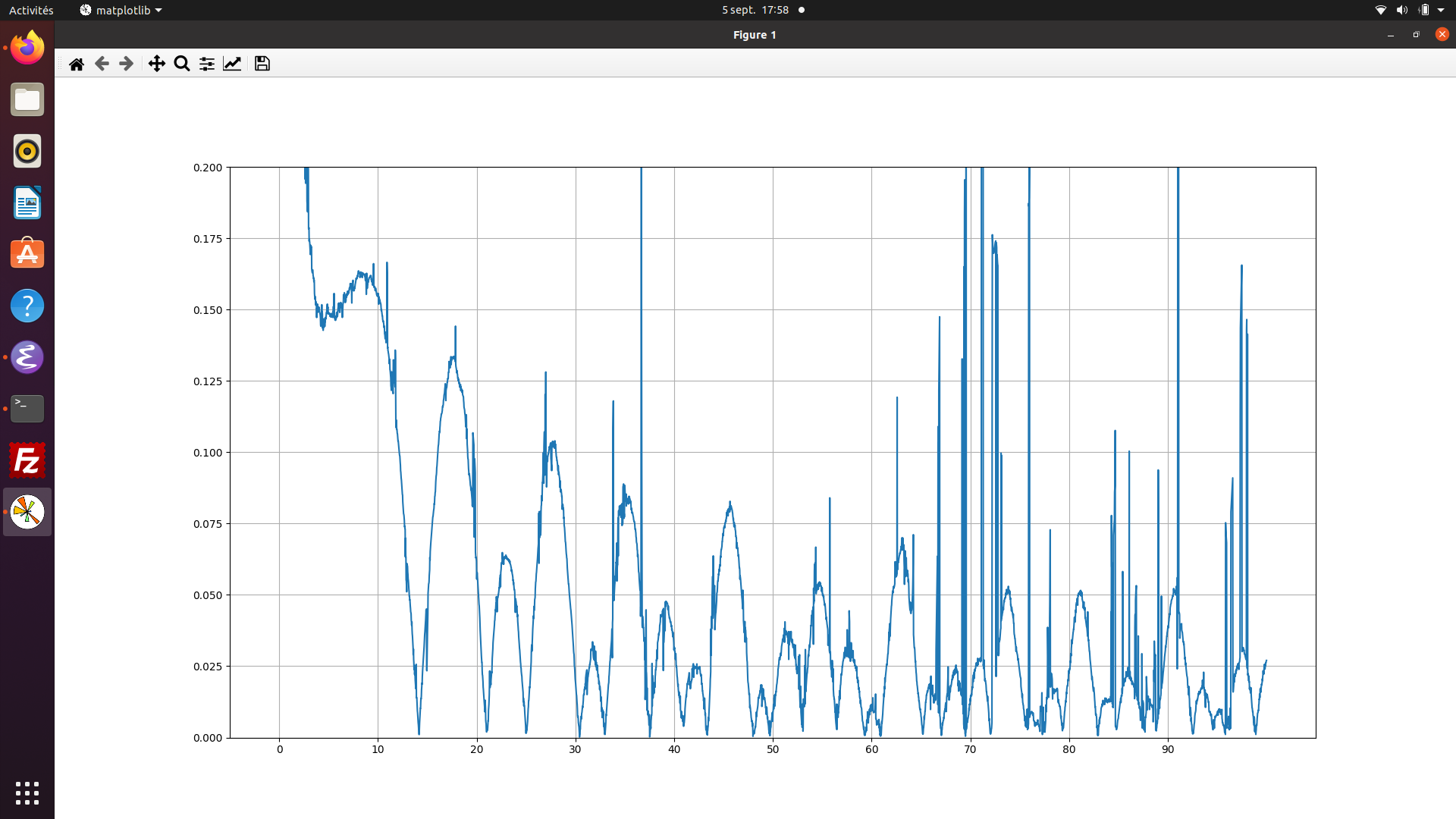 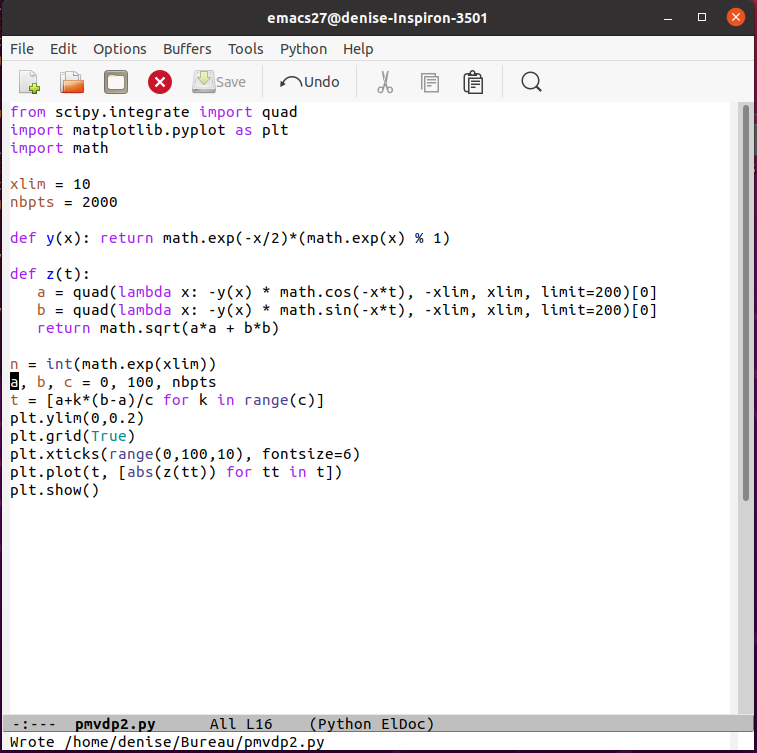
Les 3 premiers zéros de la fonction zeta de Riemann obtenus par programmation python de l’équation (9) de l’article de van der Pol de 1947
l’article à sa mémoire dans les Comptes-Rendus de l’Académie des Sciences, (Paris) 249 (1959), 1420-1422.  Le battement cardiaque considéré comme une oscillation de relaxation, et un modèle électrique du cœur Le battement cardiaque considéré comme une oscillation de relaxation, et un modèle électrique du cœur  Application du calcul symbolique ou opérationnel à la théorie des nombres premiers Application du calcul symbolique ou opérationnel à la théorie des nombres premiers  
-
27.6.2021 : double fun : composer la fonction hémi-plane (trouvée dans un article de Dirac) et la fonction inverse (trouvée dans un article de Creutz) pour envoyer tout point du plan complexe sur la droite de partie réelle 1/2 (656)
-
août 2021 : Du côté de la physique : traduction de l’article de Berry et Keating : H=xp et les zéros de Riemann
 traduction d’un article liant les zéros de zeta et les qubit à ions piégés traduction d’un article liant les zéros de zeta et les qubit à ions piégés  traduction d’un article de van der Pol de 1947 (la scie) traduction d’un article de van der Pol de 1947 (la scie)   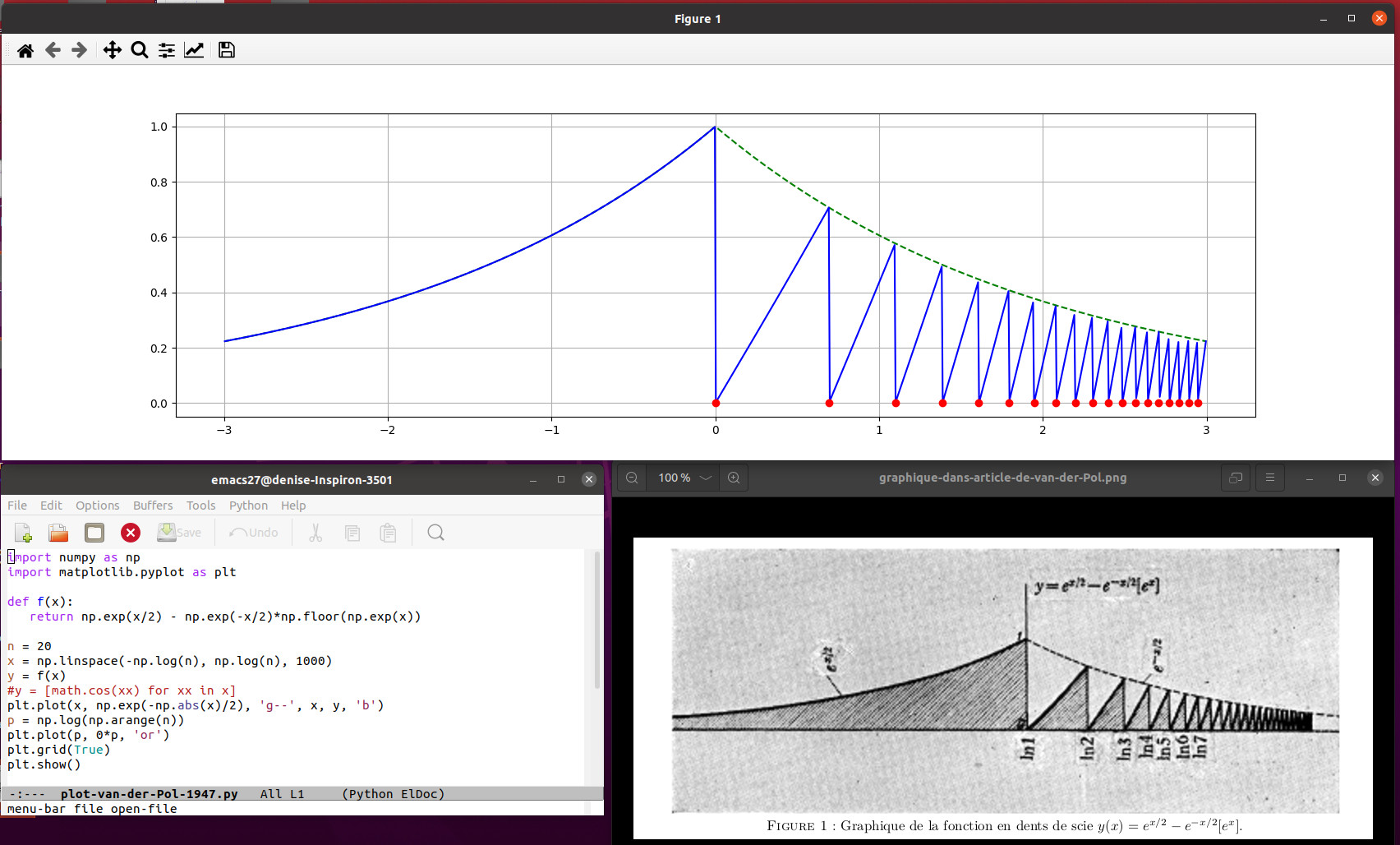
-
juillet 2021 : un zéro de zeta et son carré ont même partie imaginaire (654)
-
fin juin 2021 : lien vers un article Fun (653)
 
Juin 2023 : petite explication 
-
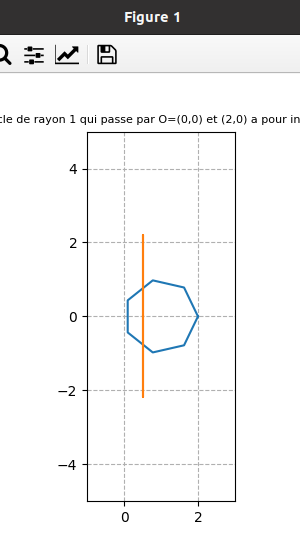
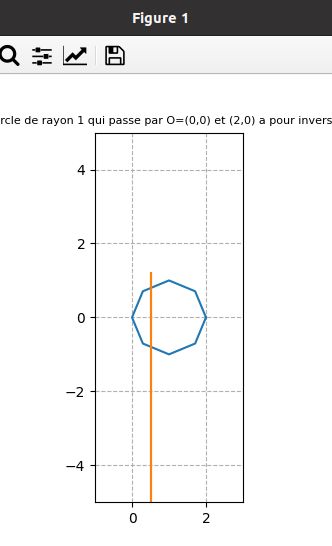
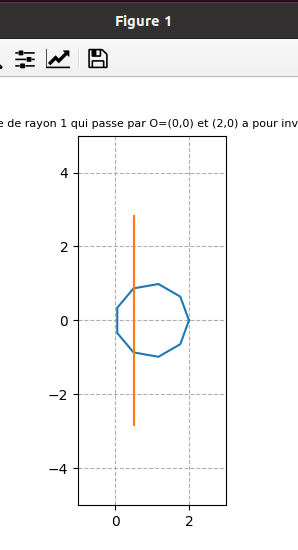
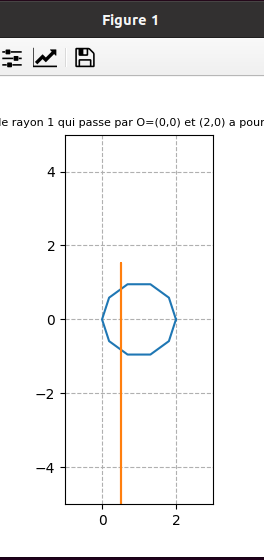
fin juin 2021 : Inverses suivant qu’on parcourt le cercle continument ou discrètement et domaine atteint (descend à l’infini pour les impairs (car l’origine est dans l’ensemble de points dont on prend l’inverse) et borné pour les pairs) (653)
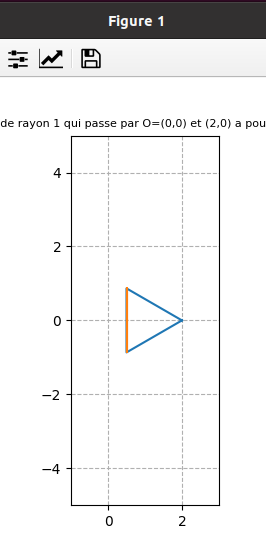 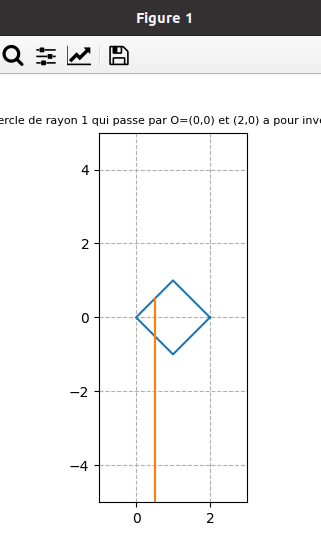 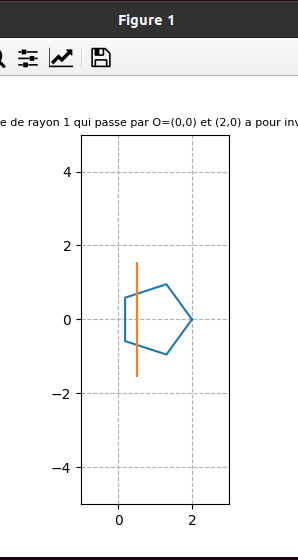 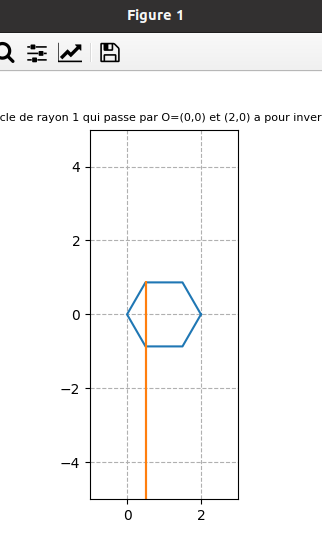      
-
13.6.2021 : Histogramme des décomposants de Goldbach (jusqu’à 100, 1000 et 10000), la barre centrale plus haute correspond aux décomposants triviaux des doubles de nombres premiers, comptés deux fois chacun. Dans les trois dessins simili-codes-barres, on a omis les décompositions triviales des nombres pairs doubles de nombres premiers. (652)
-
19.12.2021 : S’il ne devait un jour me rester qu’un seul souvenir de la conjecture (651)

-
19.12.2021 : Descente infinie (650)

-
6.11.2020 : Résumé des petites découvertes (649)

-
22.12.2020 : Affectée (ajouts) (648)

-
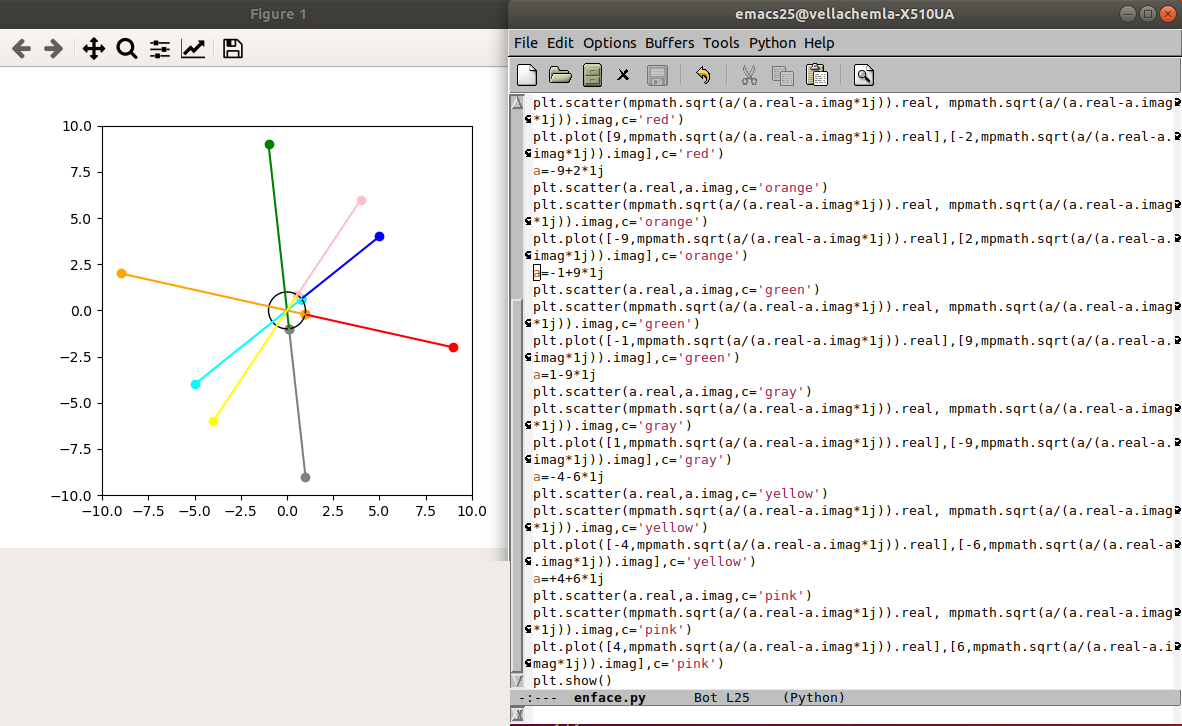
2.2.2021 : la fonction hémi-plane de Dirac (elle associe à un complexe a+ib le complexe ((a+ib)/(a-ib))^(1/2)) (647)
-
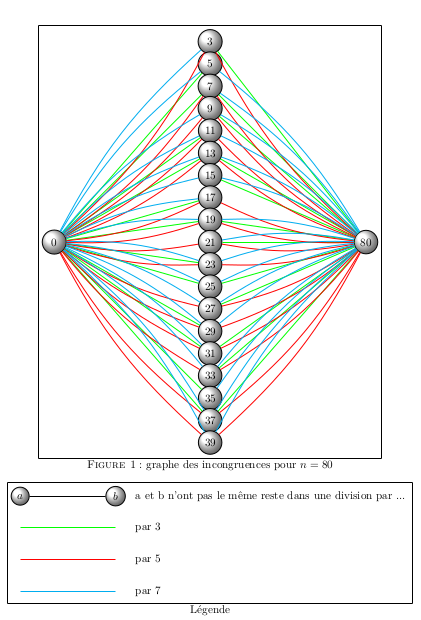
23.1.2021 : Conjecture de Goldbach et graphe biparti (646)
      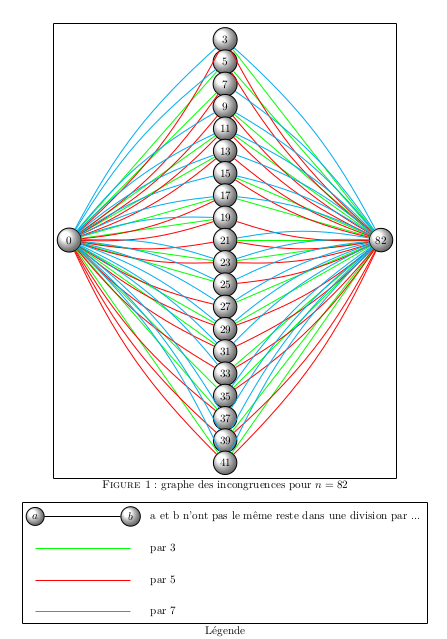 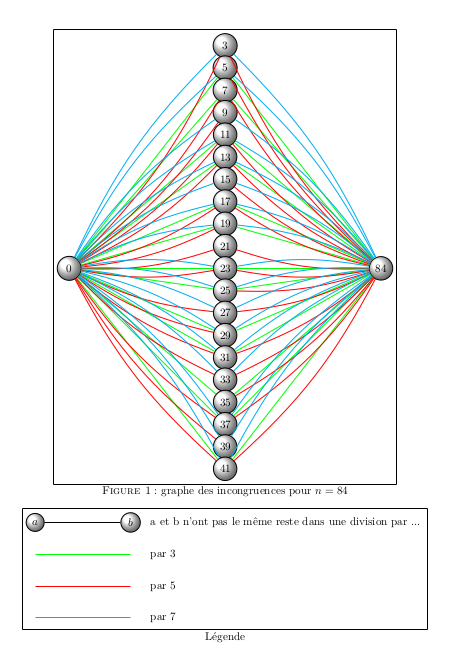
-
22.1.2021 : Conjecture de Goldbach et 2-colorations de graphes (645)

-
21.1.2021 : Groupes de rotations sur le cercle (644)

-
30.12.2020 : Liens vers les vidéos des équations-clefs de la physique
 
-
10.12.2020 : calculs divers (le python se plaint)
         12.1.2021 12.1.2021   20.1.2021 20.1.2021 
-
5.12.2020 : Trouver les décomposants de Goldbach en faisant un "détour par les log" (quand a divise b, log(b)-log(a)-log(floor(b/a)) est nul, et 0 est absorbant pour la multiplication) (643)
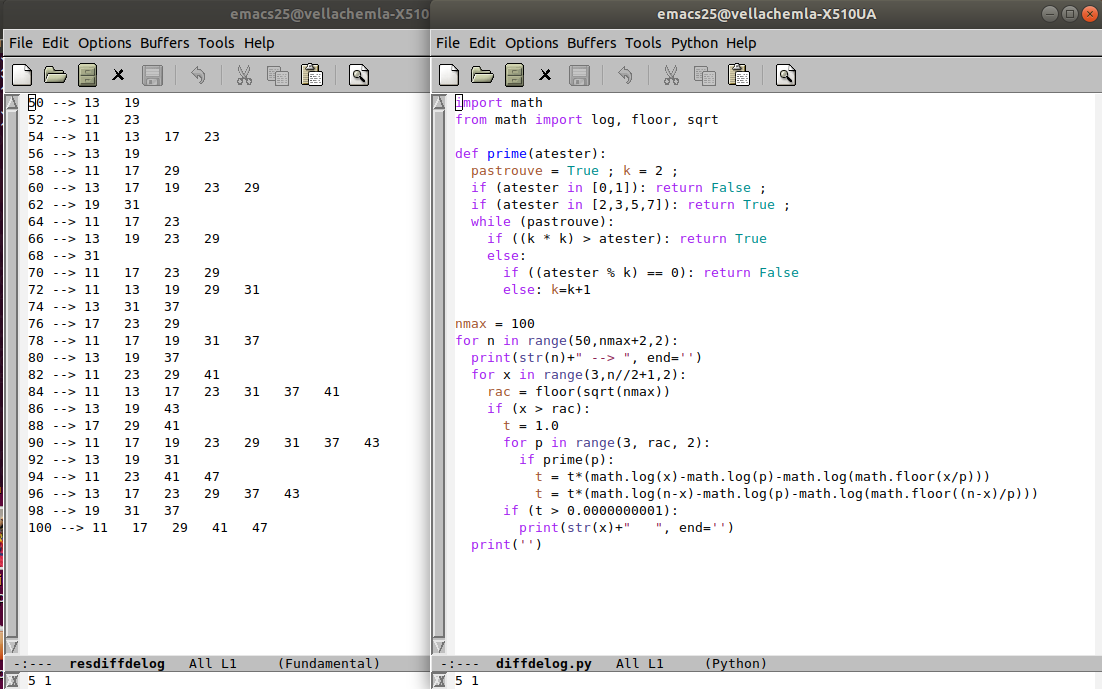
-
10.12.2020 : sans le faire exprès, j’ai obtenu un truc qui est plaisant : au lieu de voir une fonction comme qui dirait "de face", on a l’impression qu’elle est légèrement de profil, selon un certain angle (les dessins ne montrent pas en l’occurrence la même fonction mais il s’agit de faire comprendre l’idée) (642)
-
6.12.2020 : Peigne, le retour ! (641)
-
5.12.2020 : entier dans le réel (640)

-
21.11.2020 : Calcule. (639)

-
20.11.2020 : Mon professeur (CPB pour ne pas le nommer) m’avait dit : "appelez-les delta, c’est la lettre qu’on utilise pour les Dirac" (les nombres premiers sont dans les trous, 97 le dernier à droite, 5 entre les deux premiers pics, je remercie les rédacteurs de wikipedia pour l’article "diagramme de Bode") (638)
-
18.11.2020 : Mon programme est loin d’être correct, mais je trouve quand-même que par rapport à la notion de code-barre, y a d’l’idée (637)
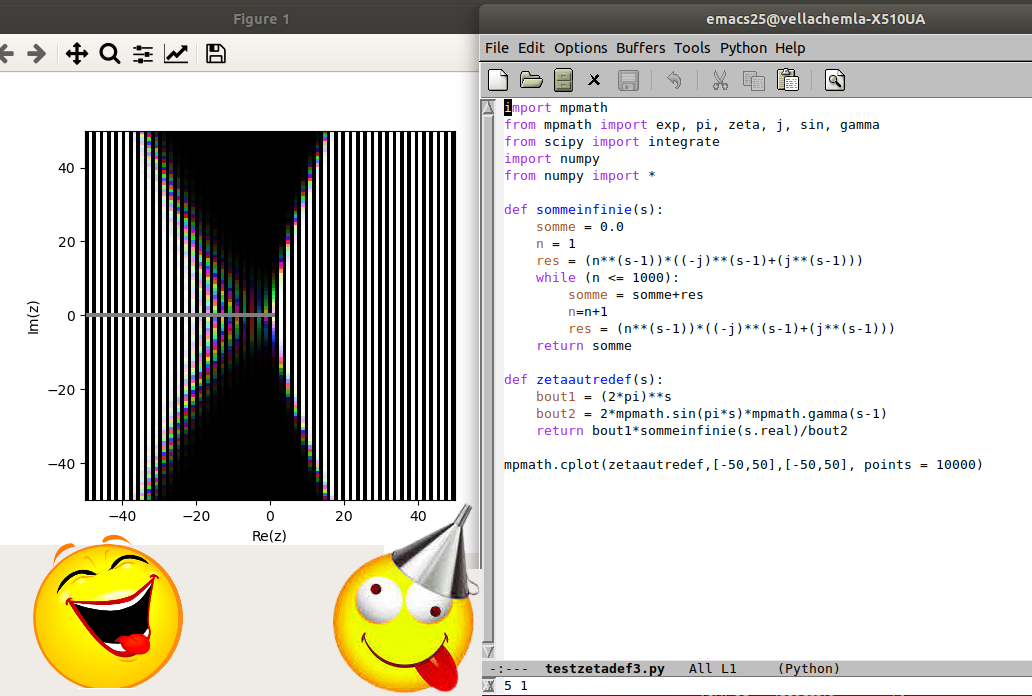
Le fait de multiplier le nombre de pixels par 10 élimine les barres du code  
-
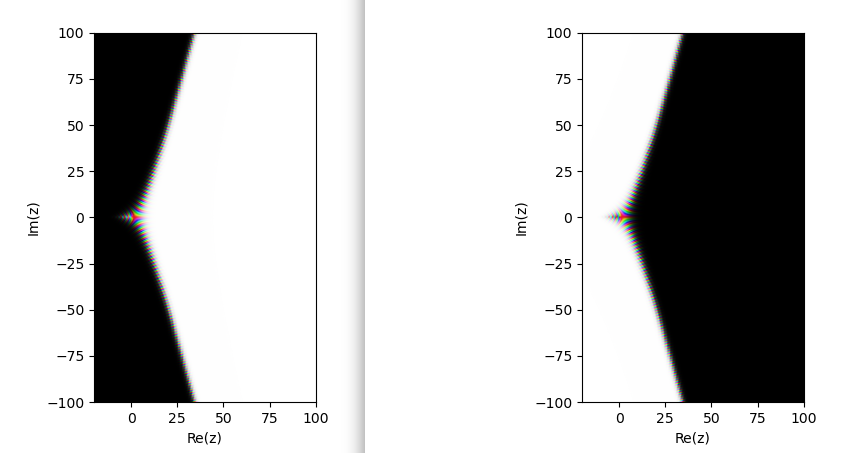
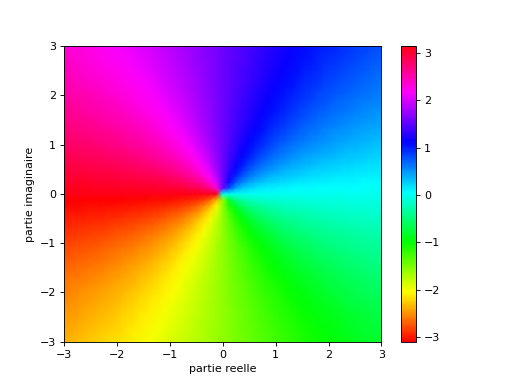
13.11.2020 : Gamma et son inverse de près, de loin, et mire des couleurs (vert inverse de bleu dans chaque dendrite, et rose inverse de jaune sur les bords externes des dendrites) (636)

-
11.11.2020 : Trouver un exemple de fonction paire qui s’annulerait en -i/2 (635)
-
avoir entendu Alain Connes présenter les idées de la géométrie non-commutative


-
8.11.2020 : Ça y est, bientôt le who is who : je viens de recevoir en cadeau d’un internaute avec qui j’ai échangé quelques messages au sujet d’un article de lui que j’ai traduit sur la fonction de Bernoulli, Peter Luschny, d’entrer dans l’encyclopédie des séquences d’entiers, l’OEIS, en citation dans la séquence A338777, le commencement de la gloire, je vous dis !
C’est là : (634)

-
30.10.2020 : Reprise valuations p-adiques (633)

-
29.10.2020 : artiste-informaticien
 Morley en asymptote Morley en asymptote  Programme exécutable en ligne ici http://asymptote.ualberta.ca Programme exécutable en ligne ici http://asymptote.ualberta.ca 
-
29.10.2020 : programmes python et leurs graphiques du Que sais-je ? (632) Les nombres premiers de Gérald Tenenbaum et Michel Mendès-France (p. 88-89)

-
21.10.2020 : 26 dessins complexes pour susciter l’imaginaire (631)
 22.10.2020 : multiples spirales 22.10.2020 : multiples spirales  
-
18.10.2020 : Inversion (630)

-
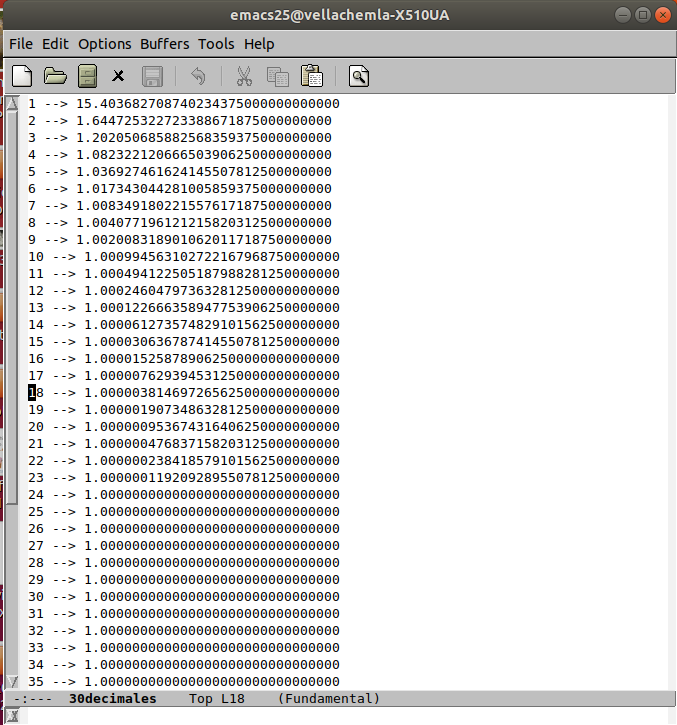
21.10.2020 : Somme des inverses des carrés et les autres (629)
-
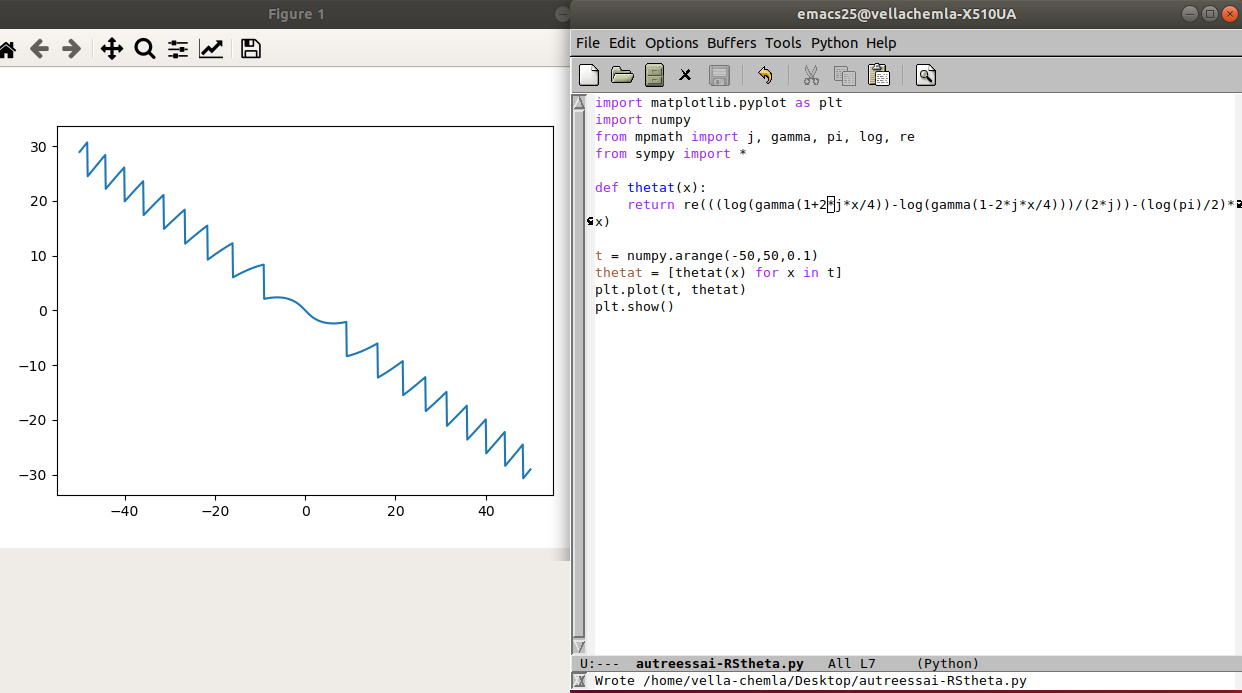
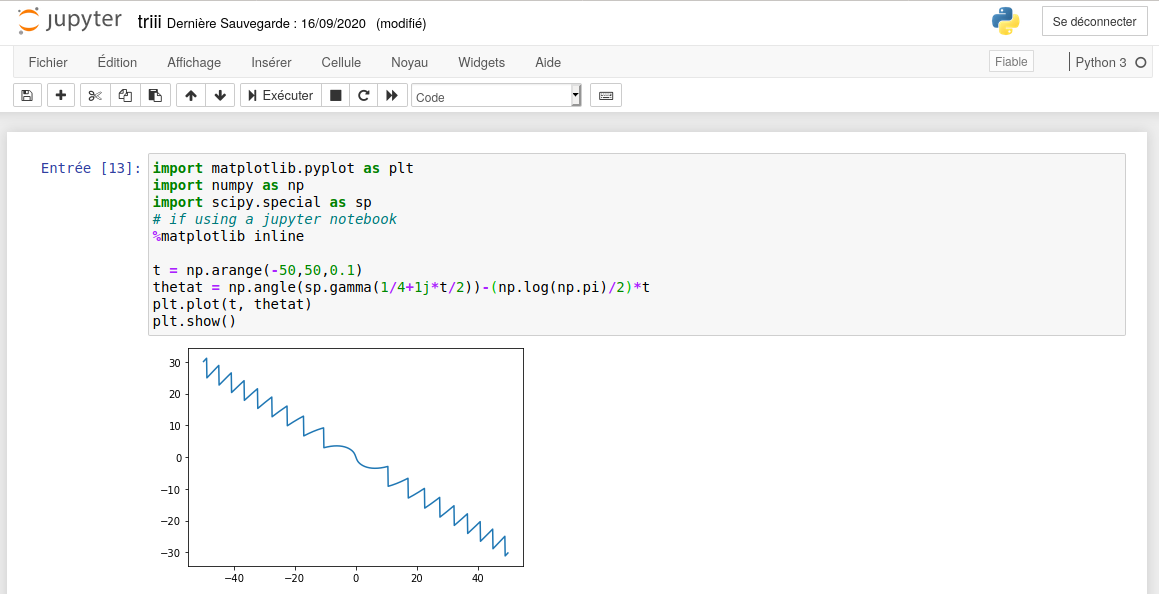
20.10.2020 : 2/3 disent la même chose
-
18.10.2020 : Inversion (628)

-
18.10.2020 : Article de Tannery sur "sa" surface, formule pour sa métrique (jupyter notebook) sur un conseil de Galliano Valent

-
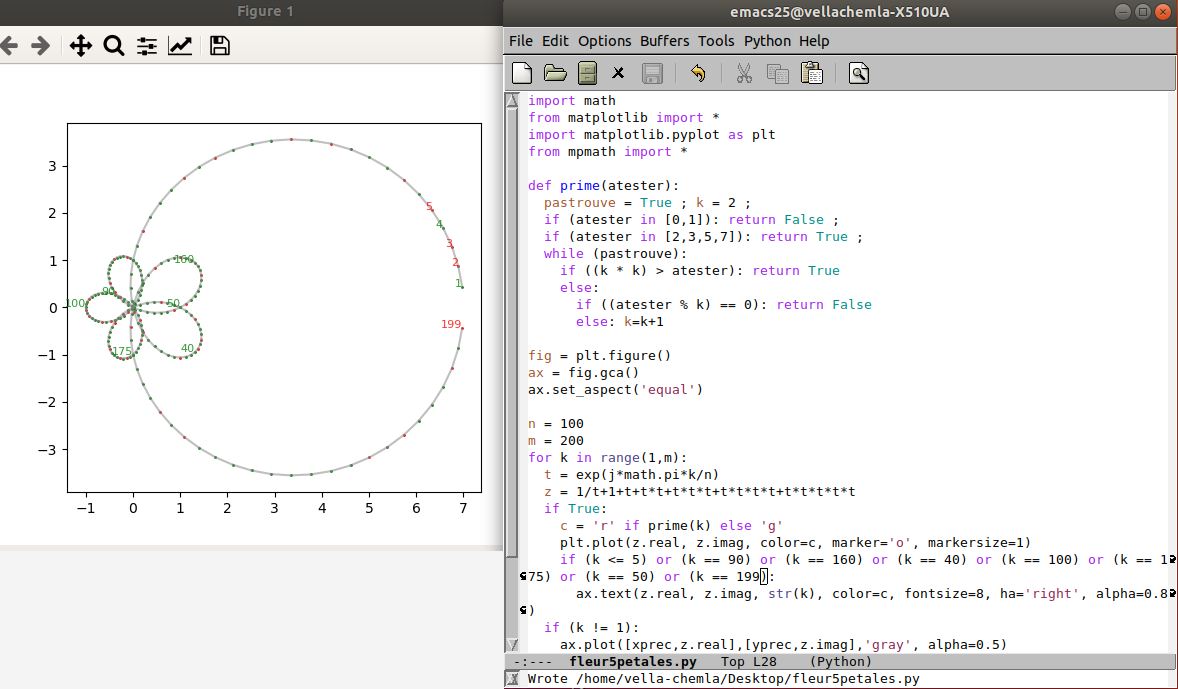
10.10.2020 : Petite étape (627)
-
Octobre 2020 : traductions d’articles ou conférences de Donald E. Knuth : Computer Science as an Art
  Dialogue avec R. Tarjan (Heidelberg Laureate Forum virtuel, septembre 2020) Dialogue avec R. Tarjan (Heidelberg Laureate Forum virtuel, septembre 2020)   Traduction d’un article récent dans Quanta magazine Traduction d’un article récent dans Quanta magazine  Art culinaire et informatique
Art culinaire et informatique  
-
8.10.2020 : D’autres dessins (626)

-
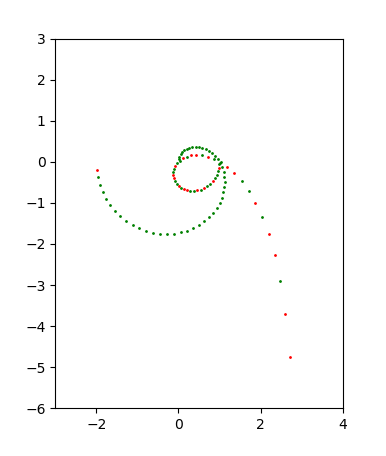
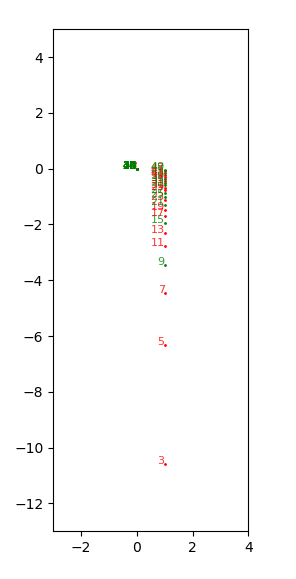
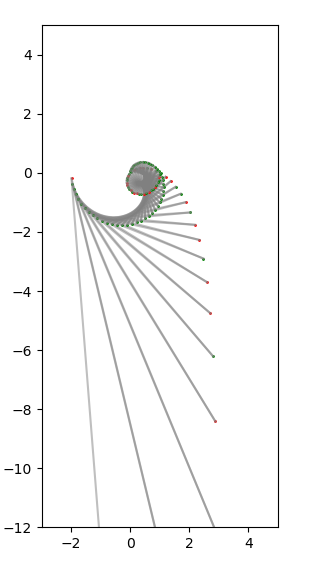
4.10.2020 : Expliquer un alignement (625)
-
3.10.2020 : Alignés par Frobenius (624)

-
27.9.2020 : Formes (623)
 
-
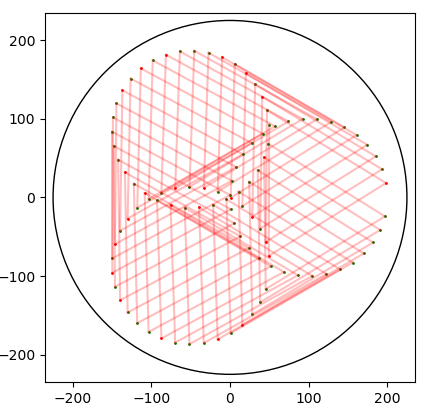
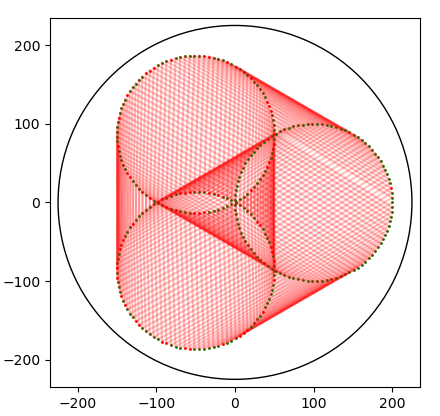
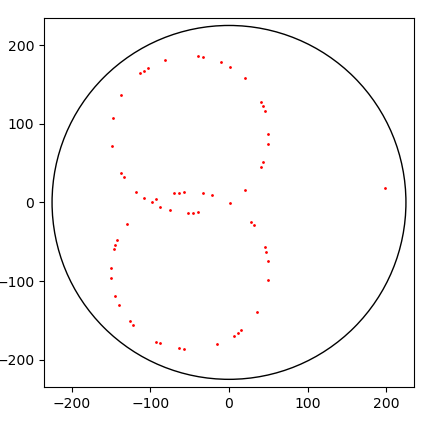
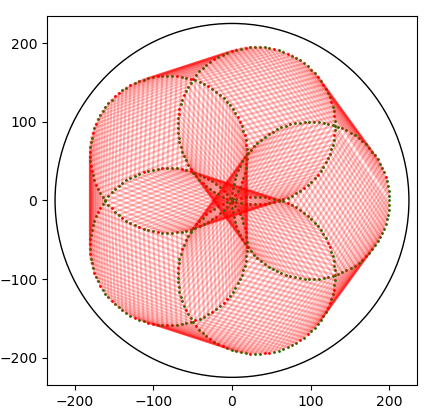
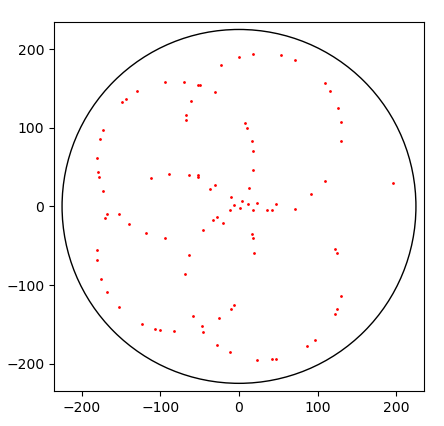
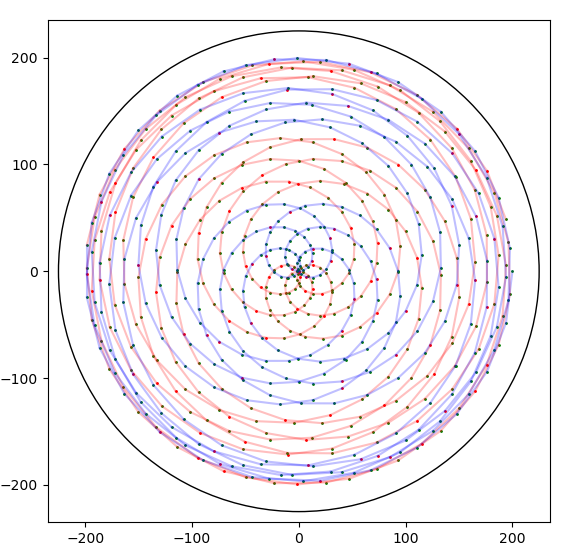
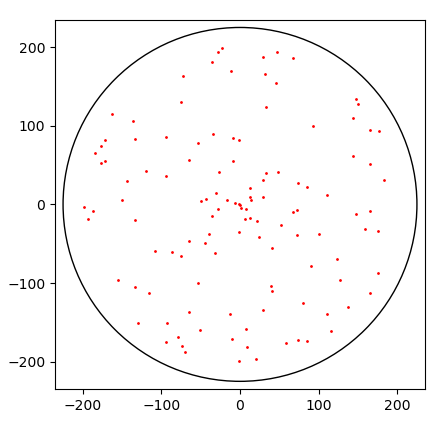
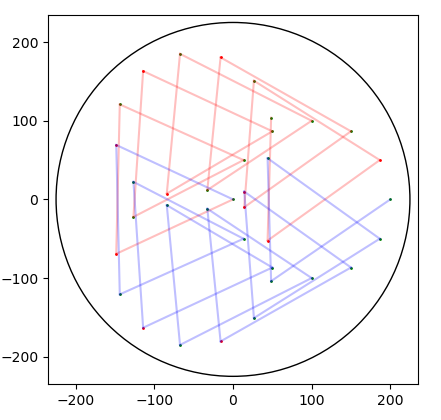
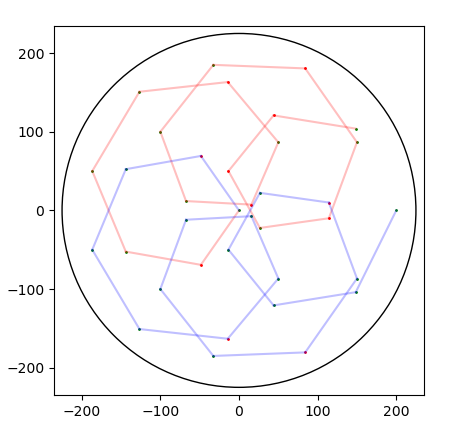
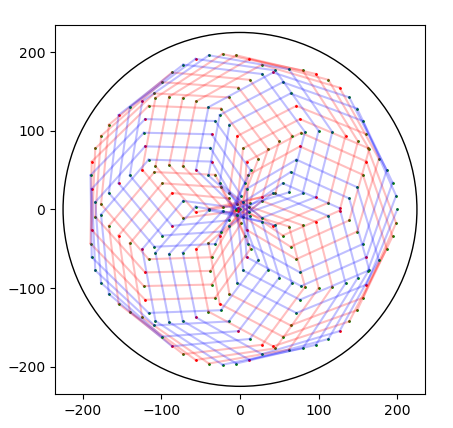
26.9.2020 : Visualiser le SNuRPF ou Système de Numération par les Restes dans les Parties Finies sous-entendu de N) : j’aimais bien le spirographe (le dernier - restes modulaires selon 7 et 36 - fait penser à un Vasarely) (622)
-
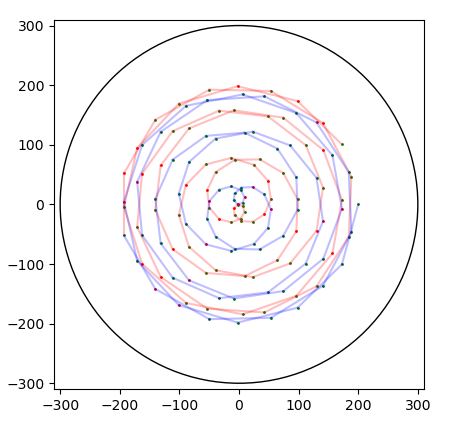
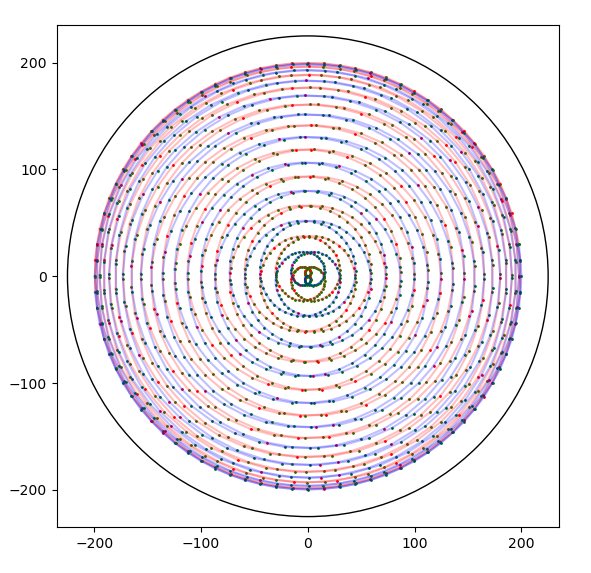
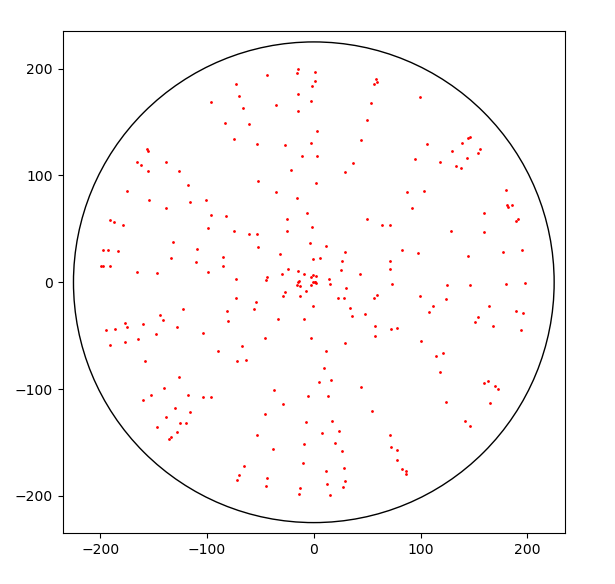
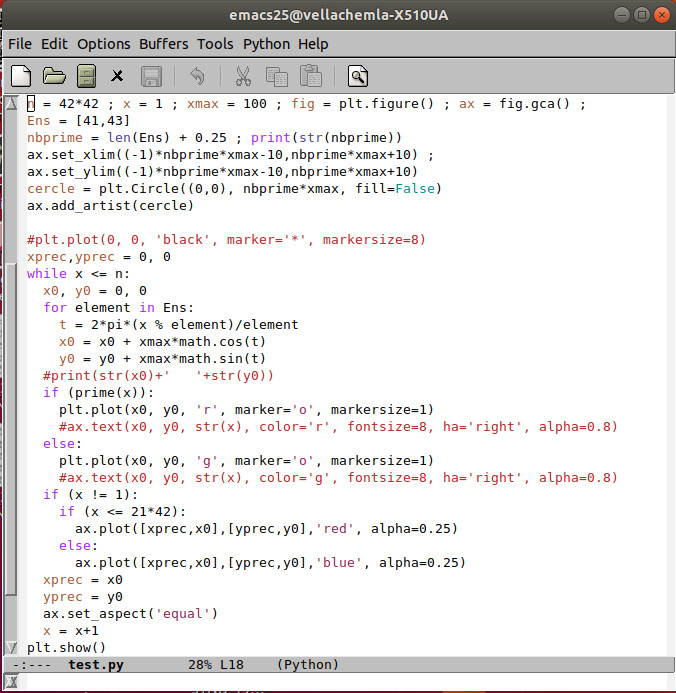
22.9.2020 : ces dessins me ravissent (621)
-
12.9.2020 : Délimiter (620)

-
9.9.2020 : Relier les nombres (619)

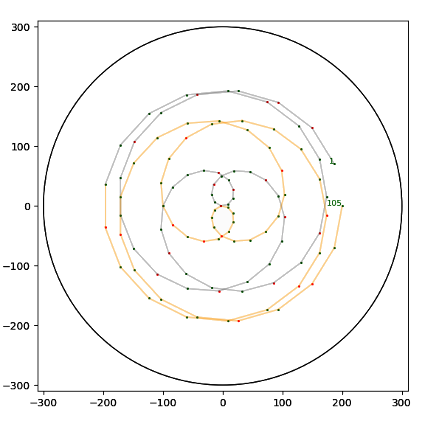
Etudier les décompositions de Goldbach par visualisations de sommes de complexes sur disque-unité 
-
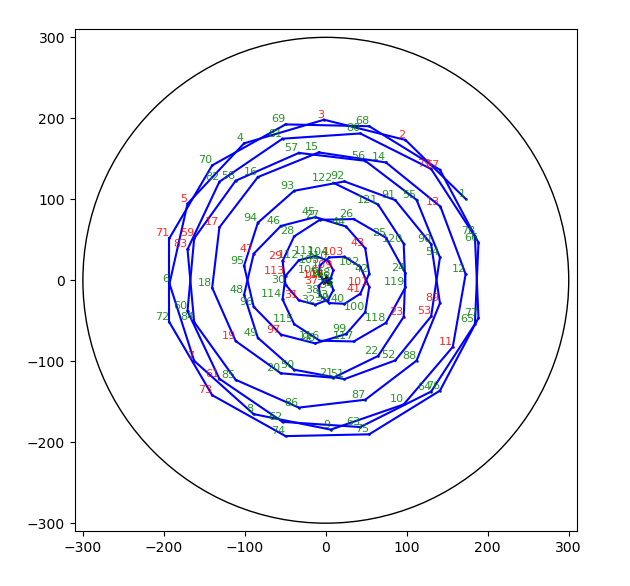
7.9.2020 : Avec 11 et 13, une spirale qui semble tendre vers 0 (618)
-
7.9.2020 : Nombres sur le disque-unité par leurs restes (617)
 
-
29.8.2020 : Calculs avec gb-tools (616)

-
21.8.2020 : Surfaces 3D : sphère (615)
 tore tore  hyperboloide hyperboloide  sablier de Tannery sablier de Tannery  pseudosphère de Beltrami pseudosphère de Beltrami 
-
20.8.2020 : Larme de Tannery en python : lorsque k=1/2√2, les géodésiques en forme de lemniscates en 3D sont fermées et elles reviennent à leur point de départ en ayant tourné deux fois autour de la surface, elles mesurent toutes 2 fois la longueur du plus grand parallèle, ou une fois la longueur d’un méridien. (614)
  article original article original    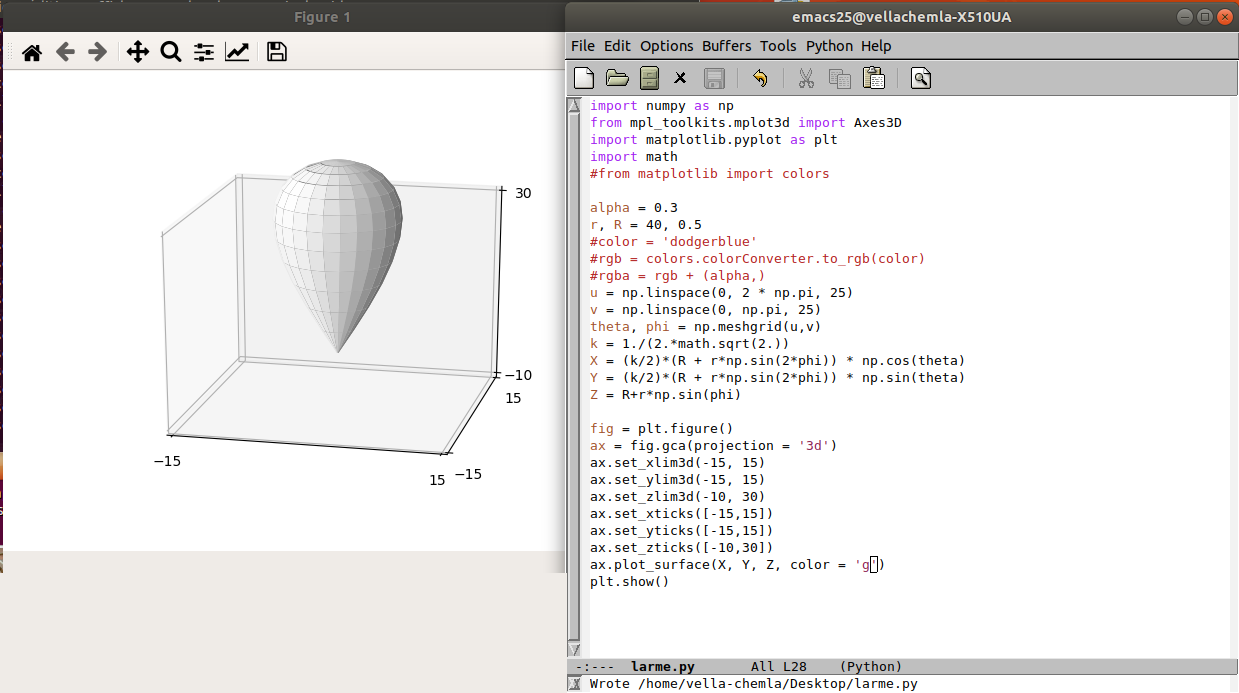 
-
18.8.2020 : Théorème de Morley et le python (vrai pour beaucoup mais pas pour la machine) (613)
  (sur trinket : (sur trinket :  ) )
-
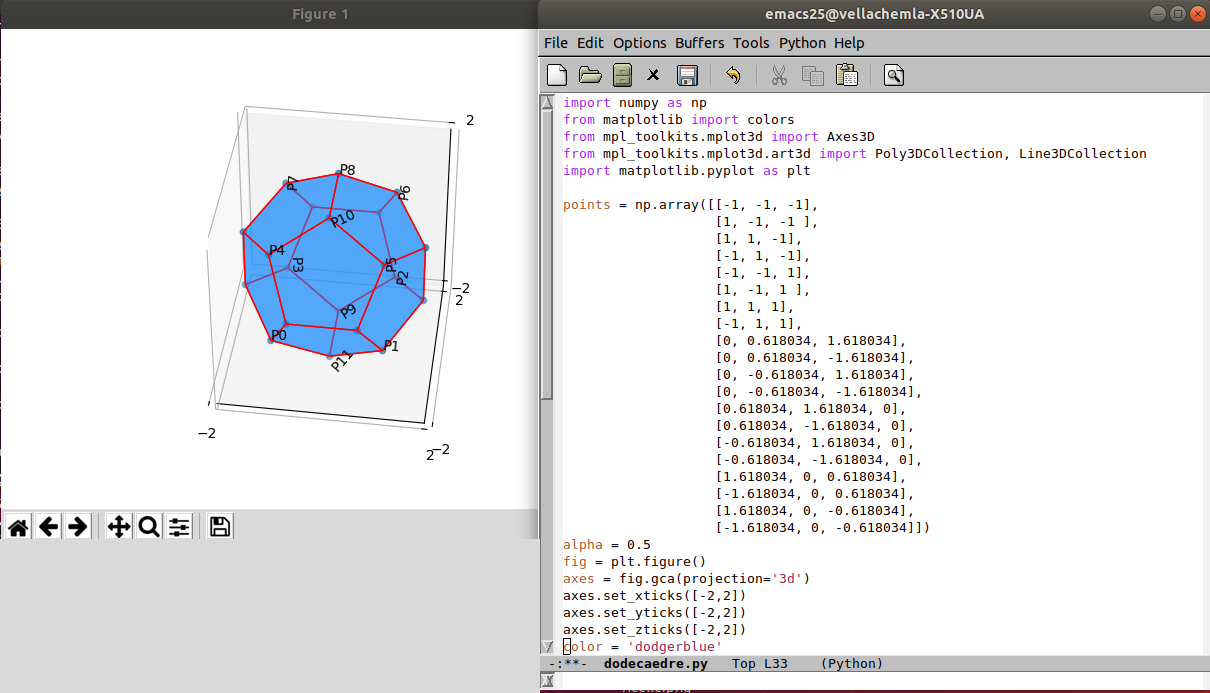
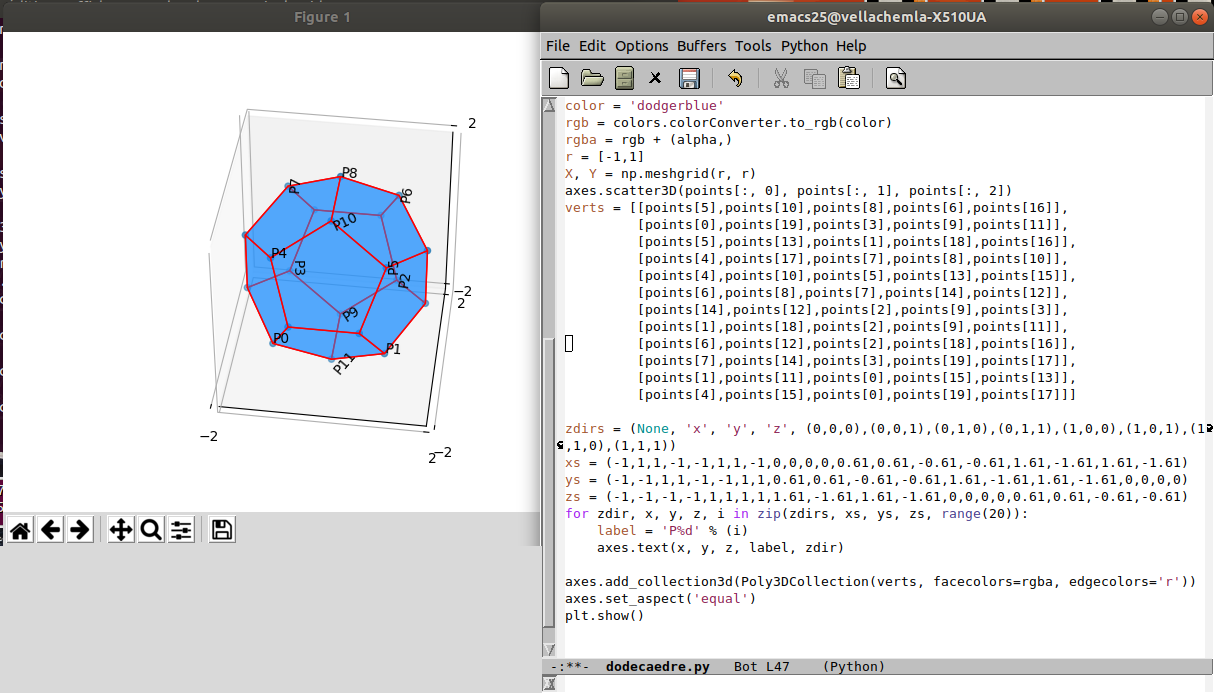
17.8.2020 : Solides de Platon en python (612)
-
10.8.2020 : Décomposants de Goldbach et algorithme d’Euclide étendu (611)

-
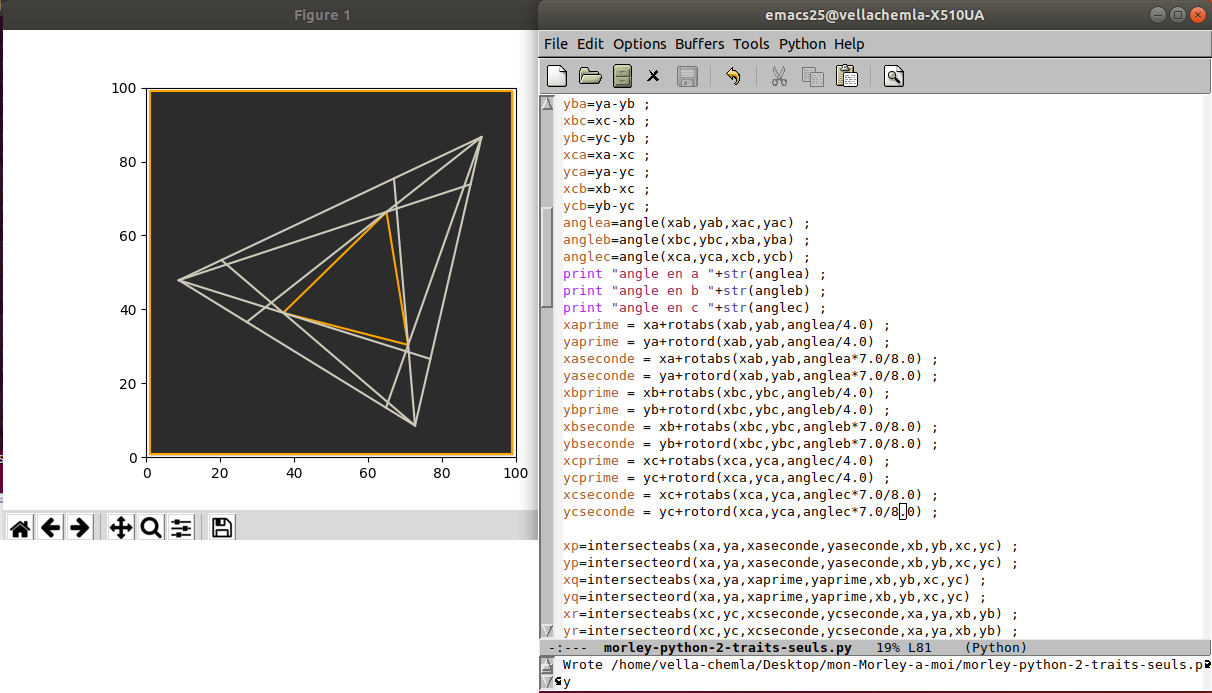
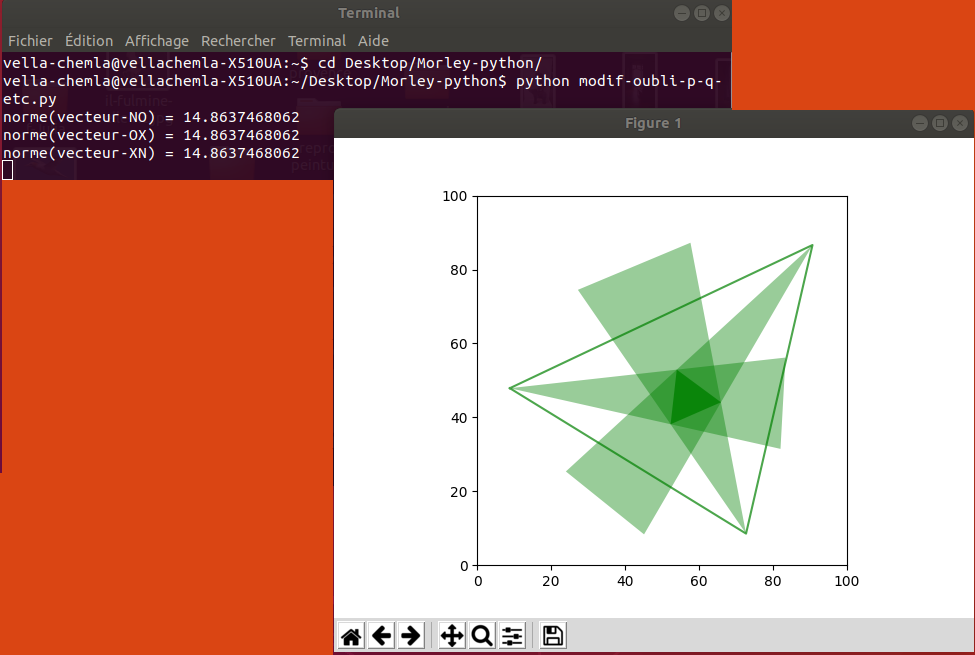
30.7.2020 : En programmant Morley, on a une première impression visuelle que c’est seulement le fait de faire le même découpage d’angles sur les 3 sommets qui importe (et qu’on pourrait par exemple faire en les 3 sommets 1/4 d’angle depuis le côté gauche et 2/3 d’angle depuis le côté droit), mais ce n’est qu’une illusion : le calcul montre qu’il est nécessaire de couper exactement en trois tiers les angles aux sommets pour que l’égalité des normes des trois côtés soit vérifiée. (610)
 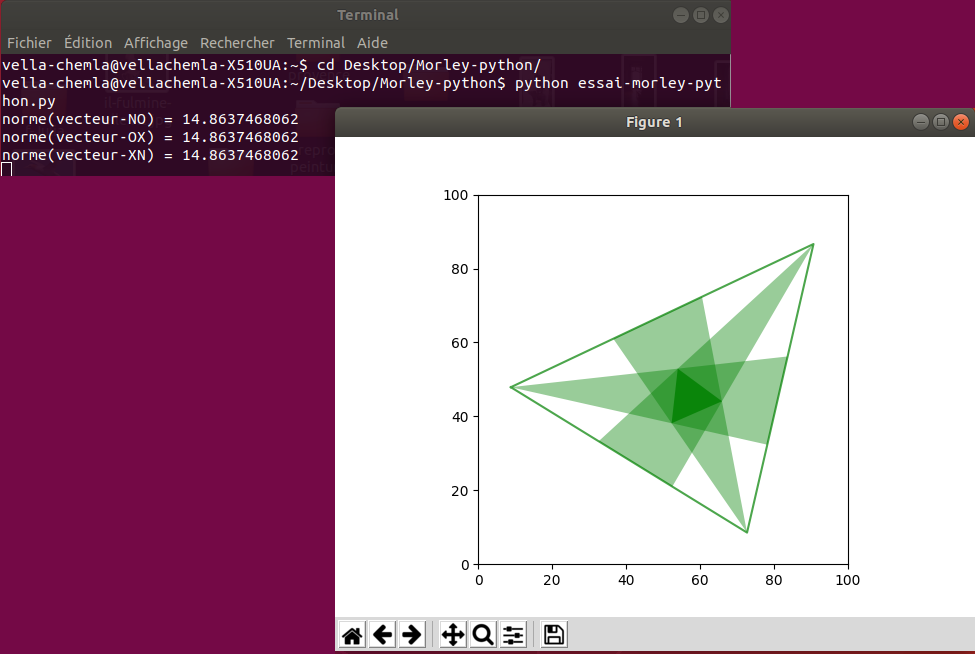
 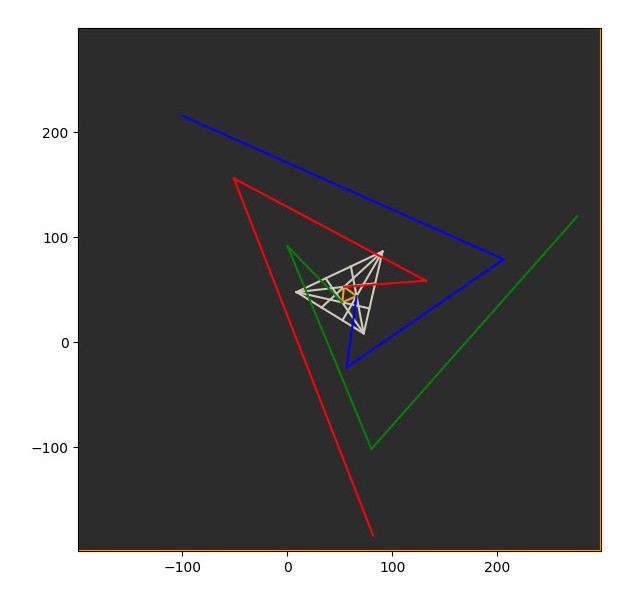
-
22.7.2020 : Paires de chaussures et douzaines d’oeufs : paquets entiers (609)

-
20.7.2020 : Triangulaires (608)

-
13.7.2020 : Décomposants de Goldbach sur cercles concentriques en Asymptote (607)
   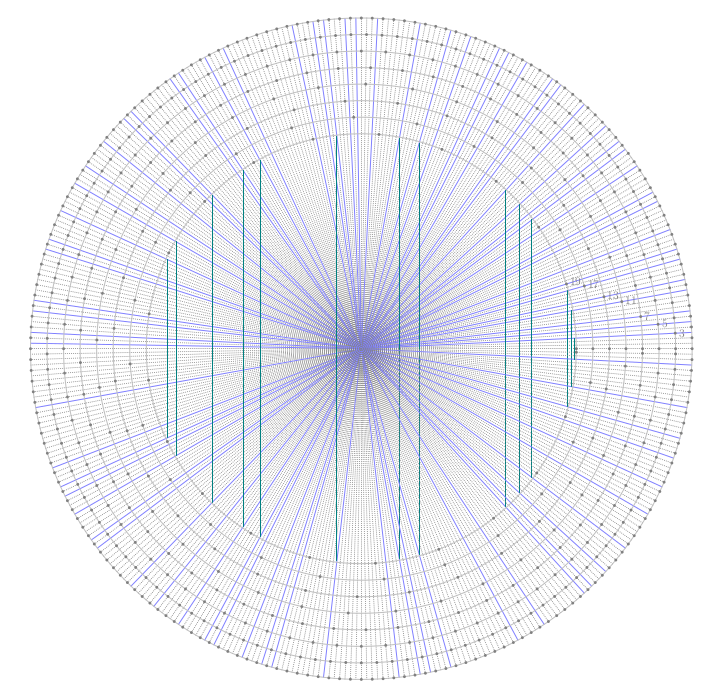
-
15.7.2020 : 10-50, c’est vraiment minuscule.

-
12.6.2020 : un transparent de l’algèbre ensembliste après lecture de Stone et Drabbe
 13.6.2020 : Treillis distributif (606) 13.6.2020 : Treillis distributif (606) 
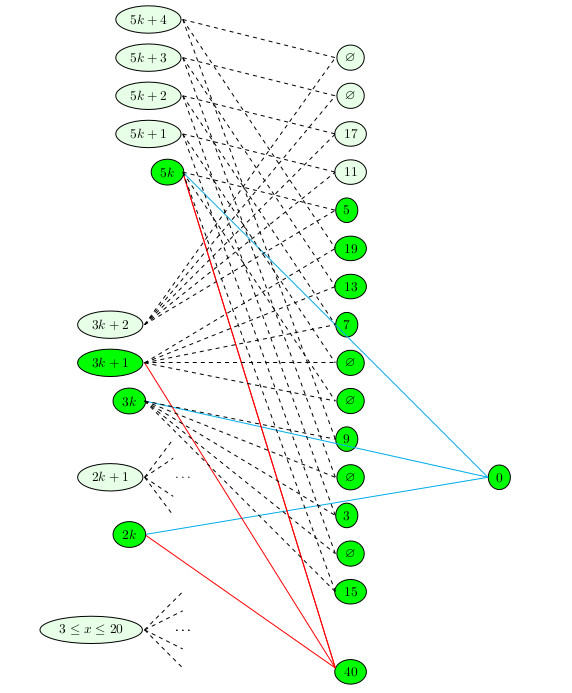
-
18.4.2020 : Ce matin, j’ai visionné le superbe film hommage à Maryam Mirzakahni Secrets of the surface, et j’y ai appris que les surfaces que j’appelais ornithologiques (parce qu’elles font penser à des têtes d’oiseaux avec leur bec) étaient dites "punctured" (pointées), le point du "punctured" étant le point à l’infini vers lequel "part" la surface. J’avais envie en mai 2019 d’associer à tout nombre premier p une surface à (p-1)/2 trous, j’avais dessiné un bonhomme de pain d’épice pour 11 (5 trous, un pour la tête, deux pour les bras, deux pour les jambes). Je me demande si le bonhomme de pain d’épice et une surface à 5 trous "à côté les uns des autres" sont une seule et même surface. J’aurais envie de "puncturer" mon bonhomme de pain d’épice au niveau du nombril, et c’est peut-être ce "départ vers l’infini" qui correspond au niveau des courbes hyperelliptiques à la partie non fermée (la partie non fermée d’une courbe hyperelliptique est en général à droite dans les visualisations habituelles de ces courbes). Je recolle le texte de mai 2019 et le dessin des interrogations...
 
-
4.3.2020 : Compter des intersections de droites (605)

-
13.2.2020 : Cristal pour trouver les nombres premiers d’écart 2 jusqu’à 600 (604)

-
7.2.2020 : Cristal pour trouver les décomposants de Goldbach de 400 (603)

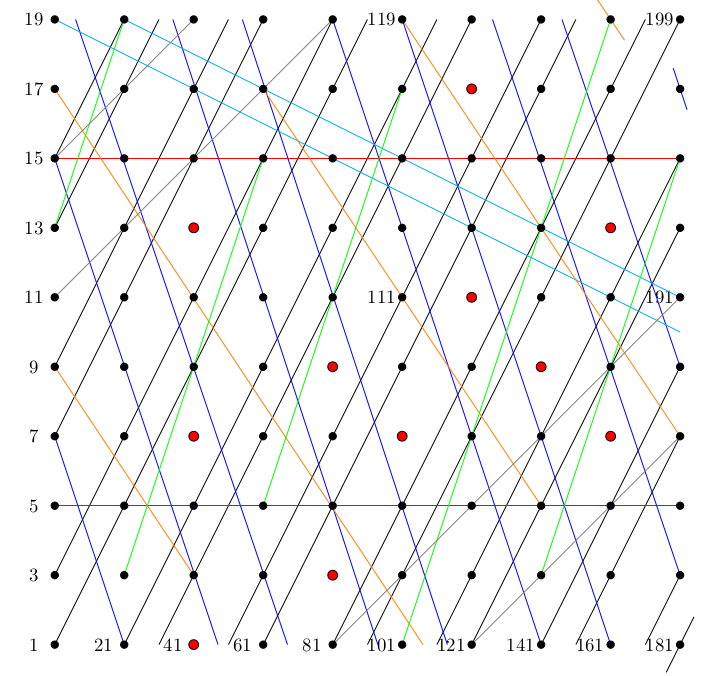
-
2.2.2020 : 8 petites vidéos sont disponibles dans la page Vidéos à destination d’élèves de CM2 (602)
-
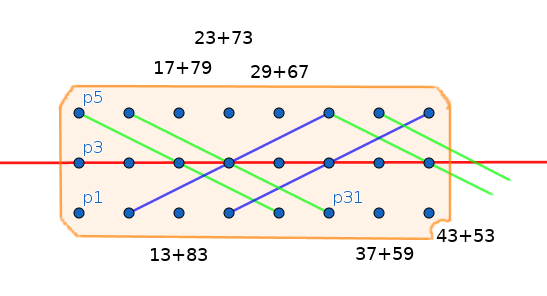
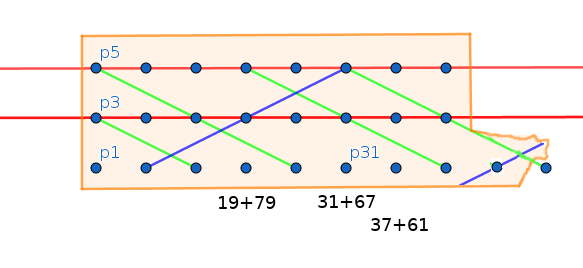
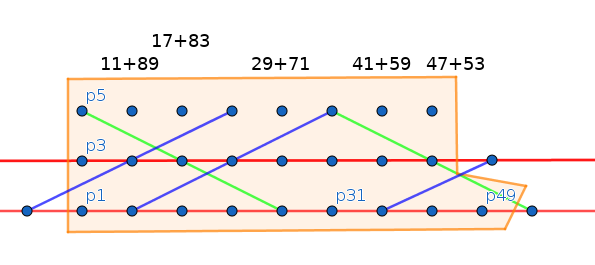
1.2.2020 : Geogebra, un outil sympa ! (601)
-
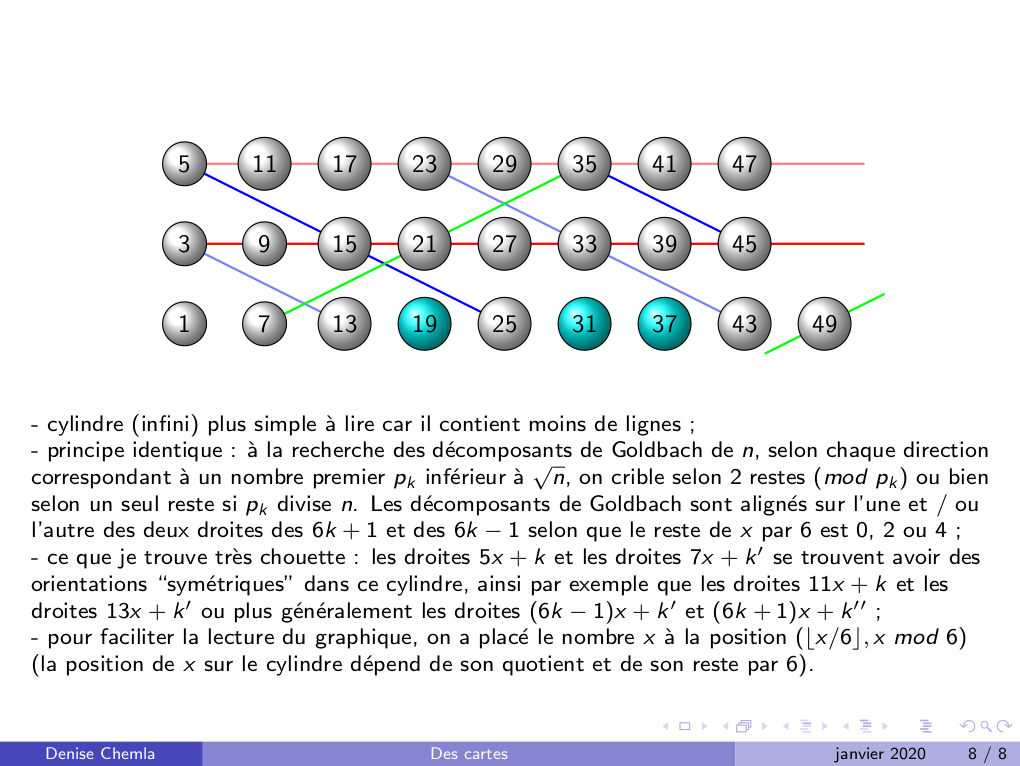
18.1.2020 : points et droites affines (600)

-
19.12.2020 : extraits de M. Croche de Claude Debussy (599)

-
♠ Décembre 2019 : Leila m’aide (598)

-
27.12.2019 : programme du problème de Peter Sarnak (minute 40’22 de la video Randomness in Number Theory (597)
 , Albert Einstein annual lecture 2019, Israël) , Albert Einstein annual lecture 2019, Israël)   . L’alternance pair - impair pour le nombre de facteurs premiers de la forme 4k+3 d’un nombre impair dont il est question est due aux propriétés de la multiplication dans ℤ/4ℤ (la factorisation d’un nombre impair de la forme 4m+3 contient forcément un nombre impair de facteurs premiers de la forme 4k+3) ; une telle alternance de parité n’existe pas pour le nombre de facteurs 4m+1 dans les factorisations des impairs successifs car le reste 1 étant neutre pour la multiplication, multiplier un nombre impair ou un nombre pair de 4k+1 conserve le reste 1. . L’alternance pair - impair pour le nombre de facteurs premiers de la forme 4k+3 d’un nombre impair dont il est question est due aux propriétés de la multiplication dans ℤ/4ℤ (la factorisation d’un nombre impair de la forme 4m+3 contient forcément un nombre impair de facteurs premiers de la forme 4k+3) ; une telle alternance de parité n’existe pas pour le nombre de facteurs 4m+1 dans les factorisations des impairs successifs car le reste 1 étant neutre pour la multiplication, multiplier un nombre impair ou un nombre pair de 4k+1 conserve le reste 1.
-
14.12.2019 : restrictions (596)

-
8.12.2019 : autre réécriture (595)
 
-
8.12.2019 : autre réécriture (594)

-
7.12.2019 : réécrire (593)

-
6.12.2019 : réécrire (592)

-
♠ 4.12.2019 : Aide de Leila Schneps (591)
 5.12.2019 : juste cause 5.12.2019 : juste cause 
-
4.12.2019 : Montrer pour ceux à qui on a fait confiance son admiration et sa reconnaissance en facilitant les recherches bibliographiques, en transcrivant, en traduisant et ce faisant, essayer d’aider au travail de tous :
J.-P. Serre  P. Cartier P. Cartier  univ. univ.  J.-P. Kahane J.-P. Kahane  J. Dixmier J. Dixmier  A. Grothendieck A. Grothendieck  A. Connes A. Connes   4 derniers articles trouvés 4 derniers articles trouvés     A. Turing A. Turing    G. Choquet G. Choquet  D’autres personnes D’autres personnes 
Index bibliographique 
-
26.11.2019 : Fibres reprisées (590)

-
24.11.2019 : Fibres, ça ne va pas (589)

-
22.11.2019 : passage courbes-graphes de triangles ? (588)

-
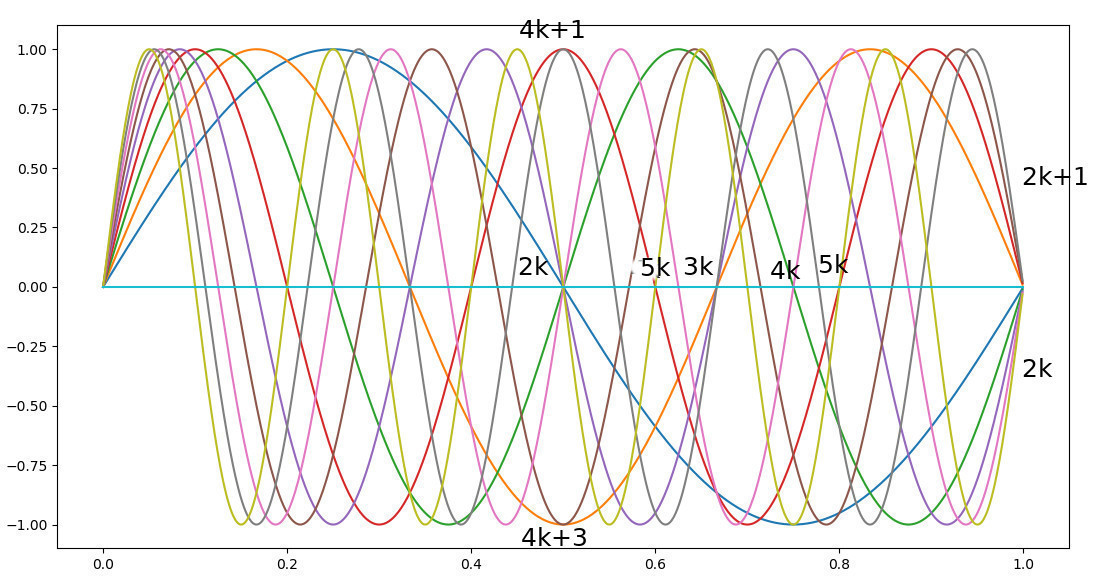
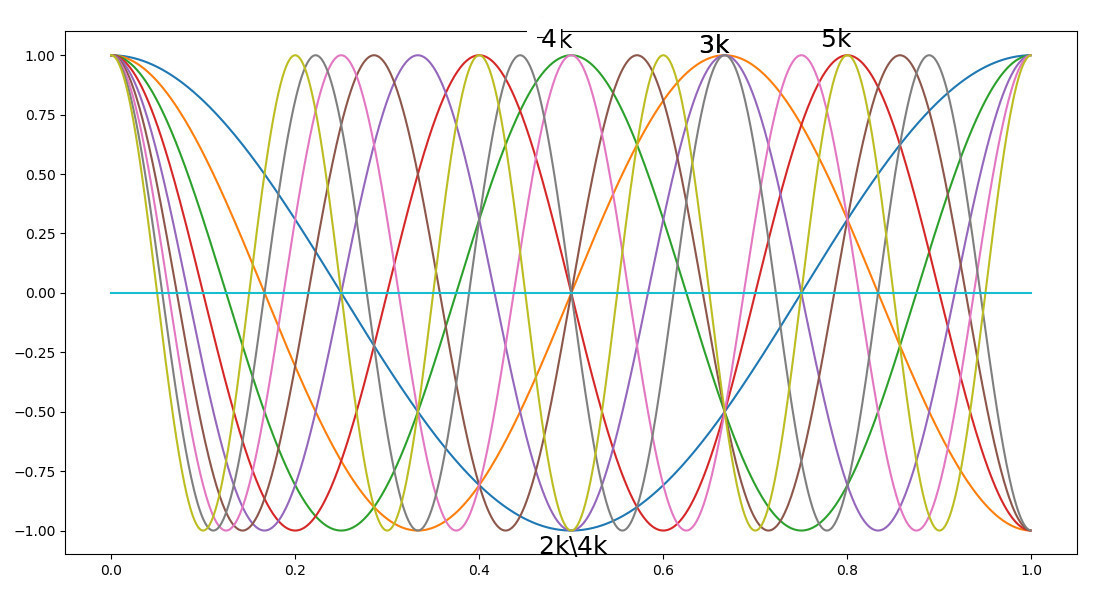
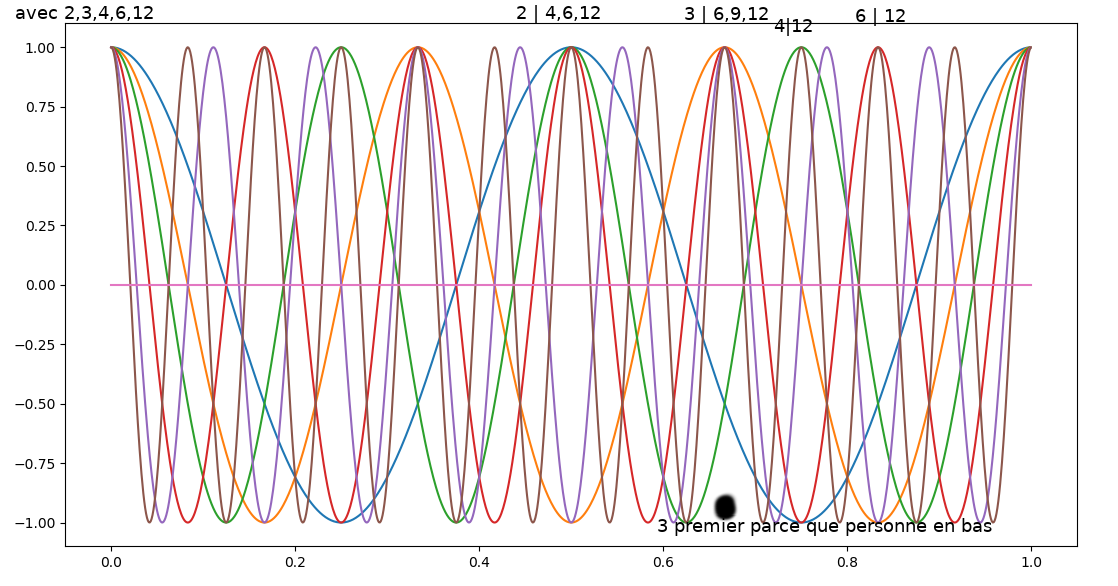
21.11.2019 : Surprise par une somme alternée de cosinus quotientés (587)
-
20.11.2019 : Au milieu, les sinusoïdes des 4k+1 se croisent en haut et les sinusoïdes des 4k+3 se croisent en bas (586)
  
-
16.11.2019 : Deviser (585)

-
13.11.2019 : Tout perdre (584)

-
10.11.2019 : Expérience de pensée ensembliste (583)

-
Traductions : (582)
- 29.10.2019 : retour aux sources (colloque fondateur de l’IA et AI@50)

- 2.11.2019 : et un très beau texte de Paul J. Cohen sur le pessimisme de Skolem

- 8.11.2019 : Histoire des mathématiques : pourquoi et comment : exposé de Weil à l’ICM 1978

- 9.11.2019 : André Weil : De la métaphysique aux mathématiques
 
-
30.10.2019 : Preuve géométrique d’Eisenstein de la loi de réciprocité quadratique (trouvé dans le livre Topologie des nombres d’Allen Hatcher) (581)
  Preuve de Lucas Preuve de Lucas  Preuve de Frobenius (en allemand) Preuve de Frobenius (en allemand) 
-
13.10.2019 : Chouettes souvenirs (580)

-
13.10.2019 : Paroles d’autres

-
28.9.2019 : Entretiens (Jacques Nimier et 8 mathématiciens : Claude Berge, André Joyal, Nicolaas Kuyper, André Lichnerowicz, Bernard Malgrange, Charles Pisot, Jacques Riguet, René Thom) avec une affection particulière pour Pisot qui parle de la conjecture de Goldbach à la page 72

-
25.9.2019 : Plaid écossais tropical (579)

-
15.9.2019 : Pgcd et Ppcm représentés sur diagrammes commutatifs (578)
 
-
31.8.2019 : si on s’intéresse aux complexes qui sont sur les 2 droites contenant les complexes de partie réelle 1/2 d’une part et les complexes de partie réelle -1/2 d’autre part, c’est-à-dire aux complexes de la forme ±1/2±bi et si on appelle m le module 1/4-b2, alors on a (1/2+bi)2=m+bi ; on a aussi (1/2-bi)2=m-bi (dans les deux cas, l’argument est conservé par l’élévation au carré) ; (577)
mais on a (-1/2+bi)2=m-bi, et on a (-1/2-bi)2=m+bi (dit rapidement, l’élévation au carré conjugue les arguments).
Quelle valeur prend ζ lorsqu’on l’applique au carré d’un nombre complexe (i.e. que vaut ζ(s2) ?).
A-t-on une expression de cette valeur en fonction de la valeur de ζ(s) ?
-
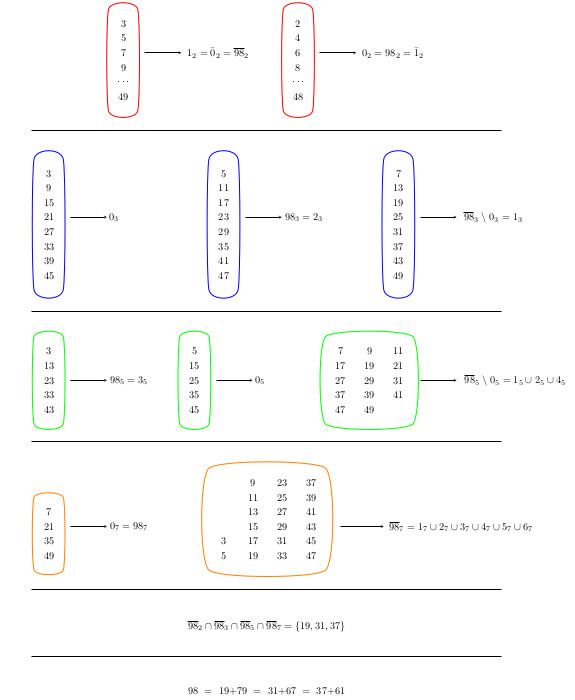
23.8.2019 : Ensembles (576)
-
♥♥ 10.7.2019 : un ensemble, une transformation, des traces de premiers (575)
 
-
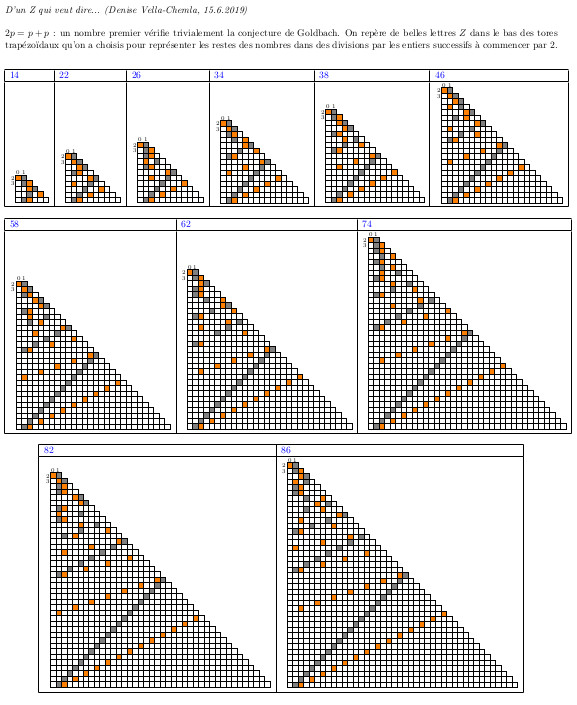
15.6.2019 : d’un Z qui veut dire... (574)
-
15.6.2019 : matrices circulantes (573)
 
-
12.6.2019 : On n’aura qu’à l’appeler le tore trapézoïdal (572)
-
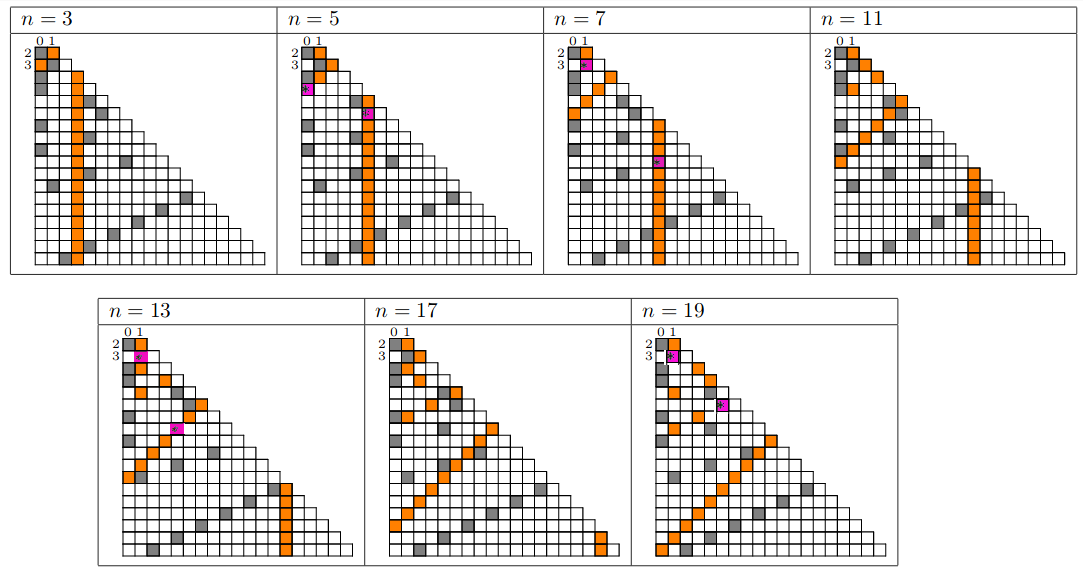
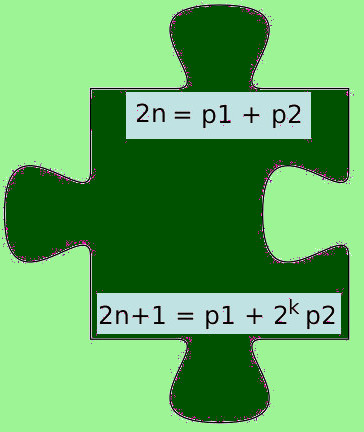
5.6.2019 : Conjecture de Goldbach et les impairs (571)
-
31.5.2019 : Ô stop ! (570)

-
30.5.2019 : Colliers de décomposants (569)

-
22.5.2019 : Colliers (568)
 
-
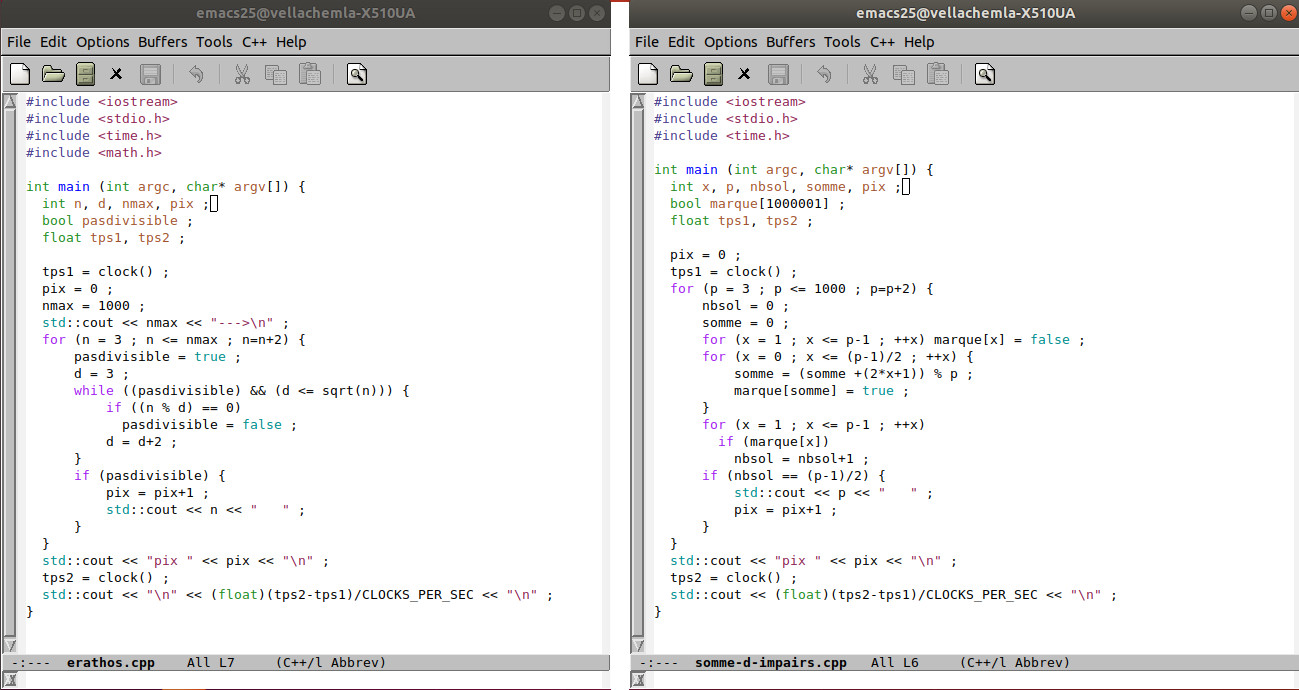
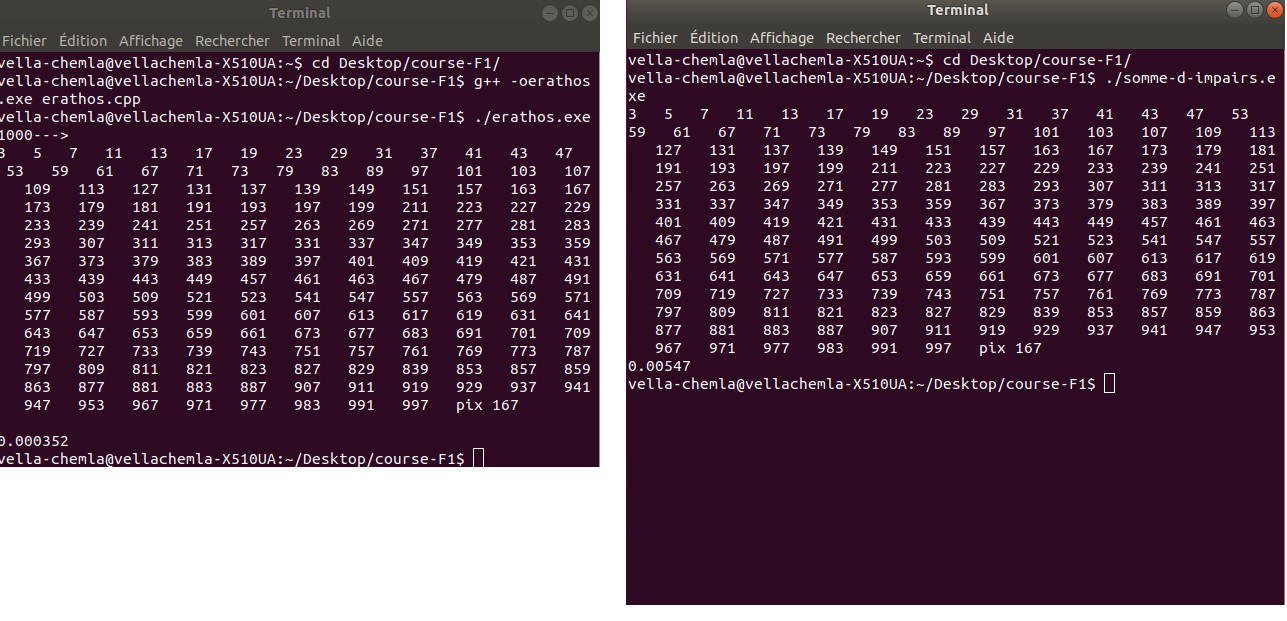
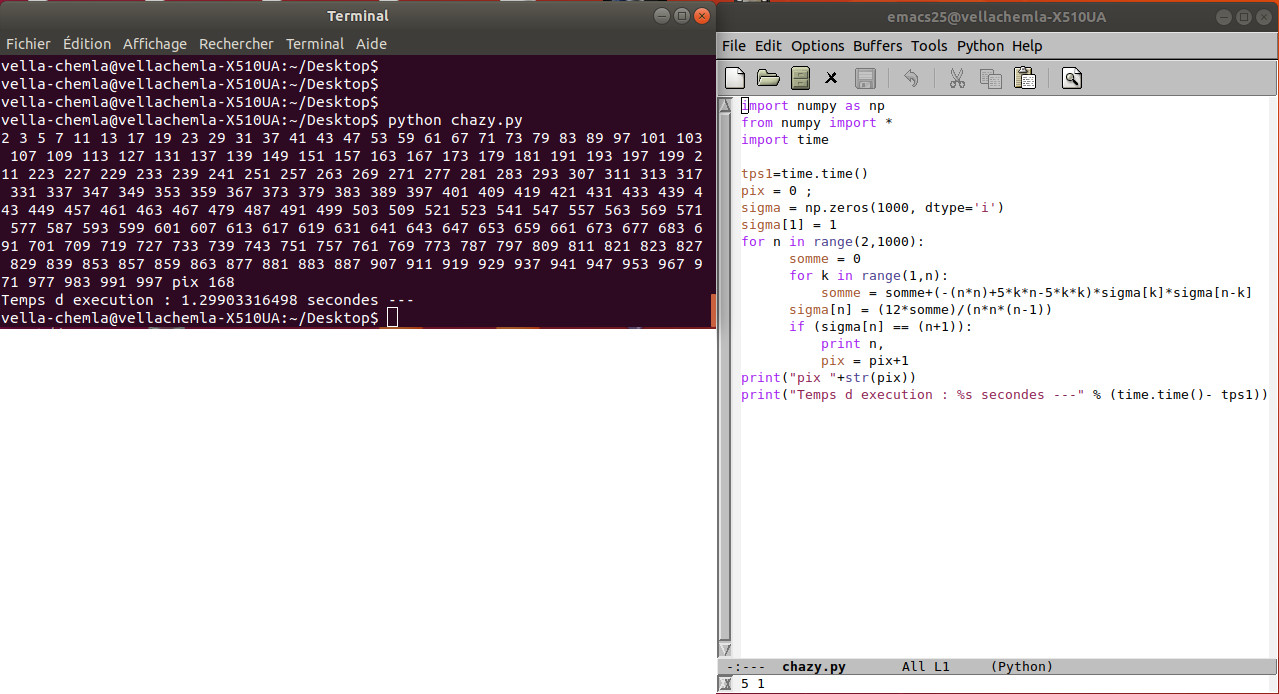
21.5.2019 : crible d’Eratosthène, sommes d’impairs, découverte d’Euler, différence de sommes de parties entières ? (567)
-
19.5.2019 : nombres premiers et aires dans un carré (566)

-
19.5.2019 : nombres premiers et résidus quadratiques des Recherches arithmétiques (565)

-
18.5.2019 : Des puissances et des palindromes (564)

-
16.5.2019 : Grouper par 4 (563)

-
11.5.2019 : caractérisation topologique des nombres premiers 4k+3 (562)
 
-
9.5.2019 : retour aux polynômes de Tchebychev et aux indices de Gauss (561)

-
7.5.2019 : Premiers 4k+1 de Gauss, sommes d’une seule manière de 2 carrés d’entiers (Fermat, Euler) (560)
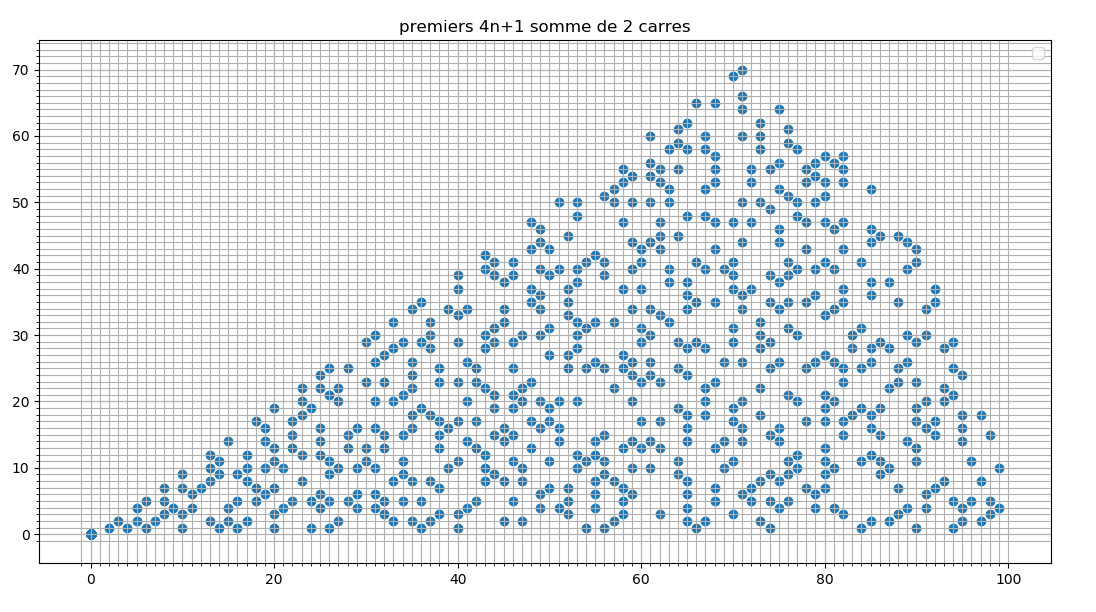
en rouge plus petit  Section 182 des Recherches arithmétiques de Gauss traitant de ce sujet
Section 182 des Recherches arithmétiques de Gauss traitant de ce sujet  ![]()
-
4.5.2019 : points presque entiers sur spirales logarithmiques en python (559)
 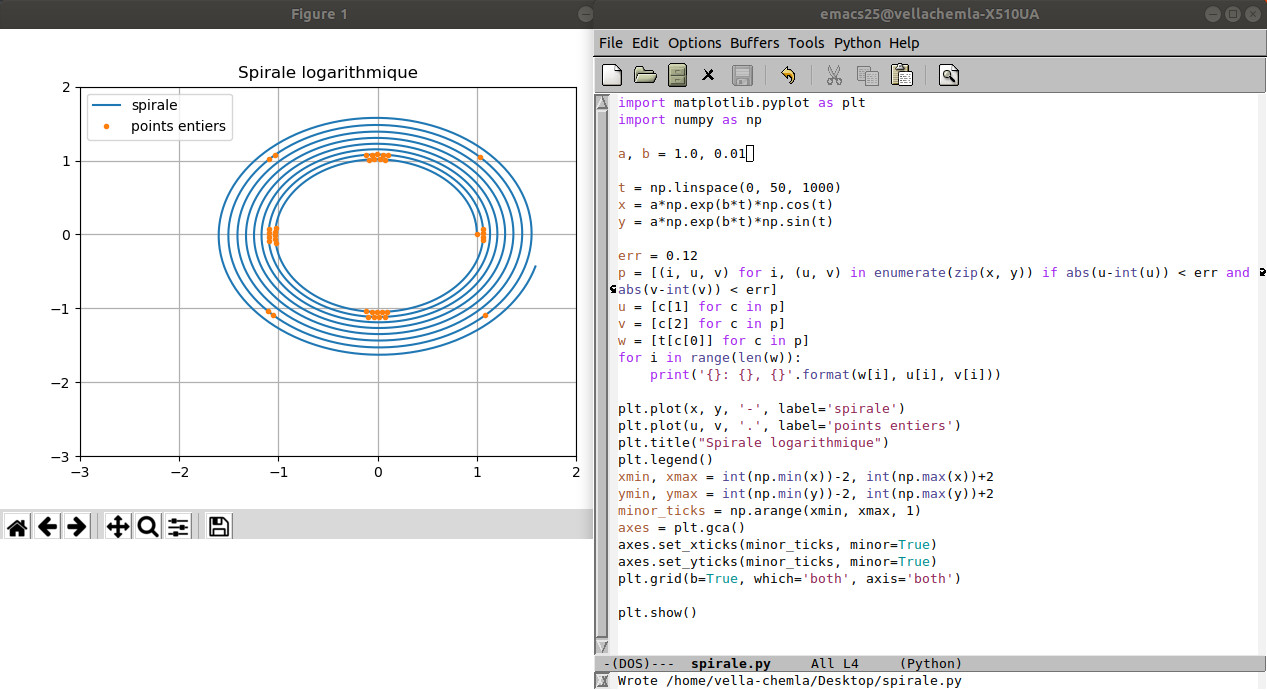 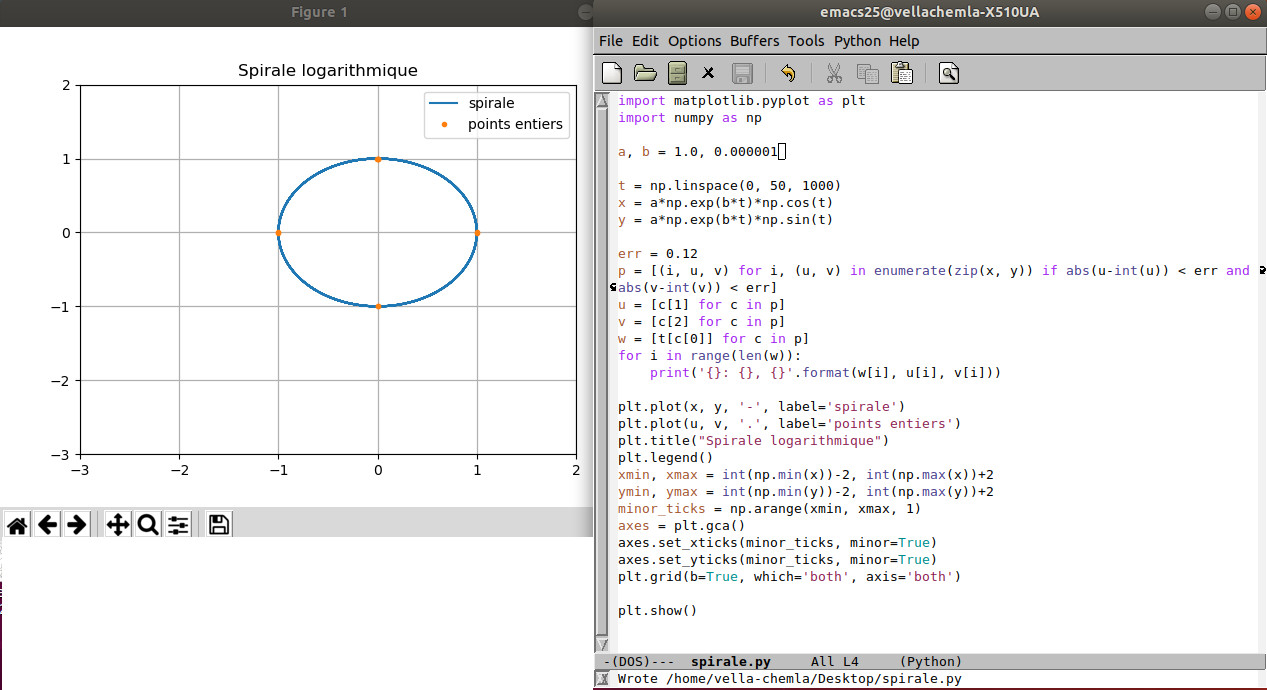
132=122+52 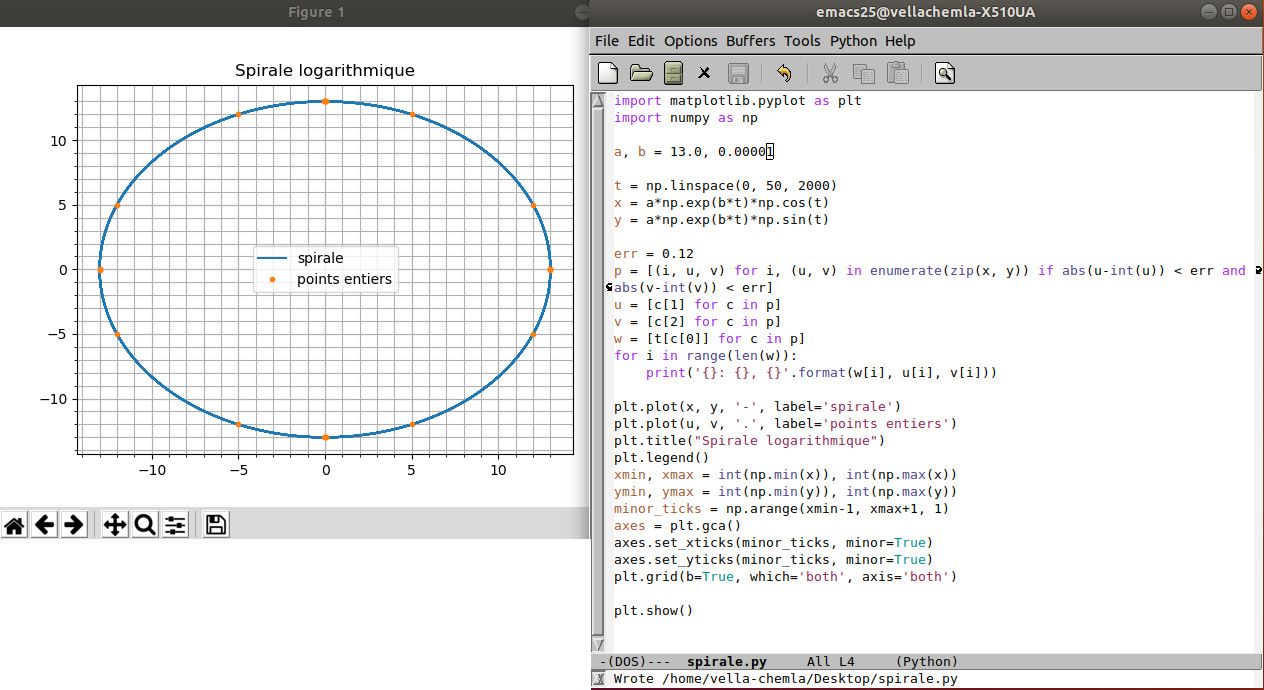
(pour voir 3 et 2 dans 13, cf. Quelques propriétés des carrés parfaits sur Images des mathématiques)
-
2.5.2019 : variations de la fonction qui s’annule pour les premiers (la seconde en divisant les cosinus par leur argument) (558)
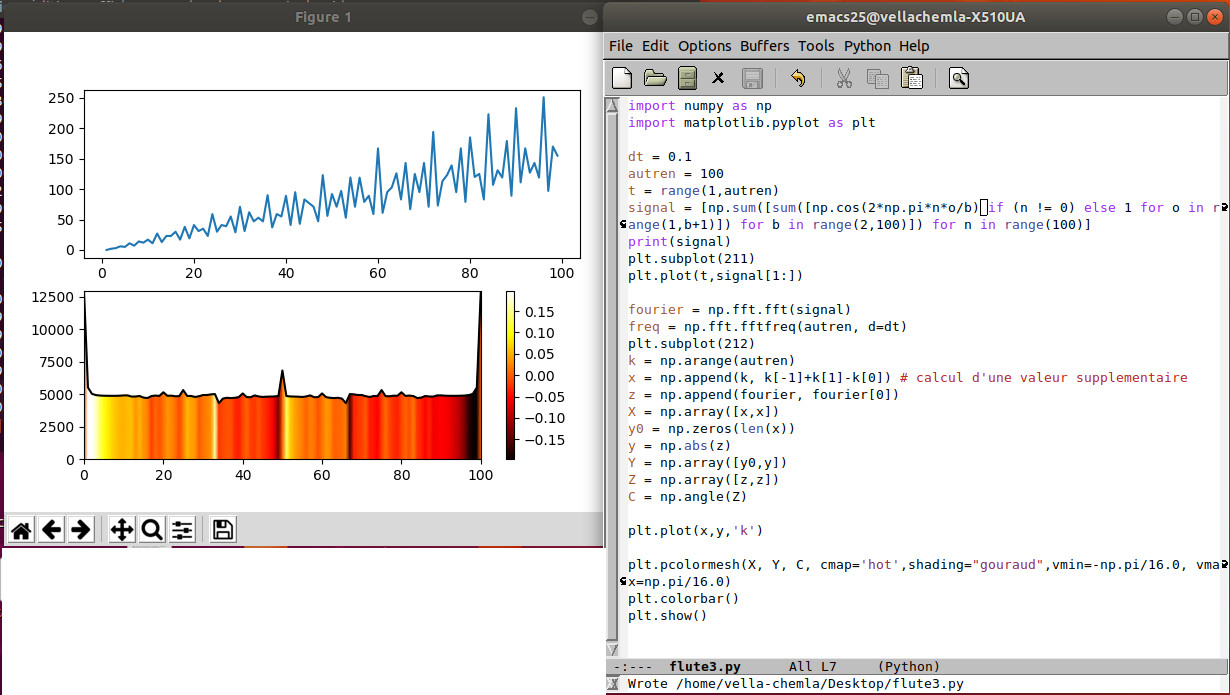 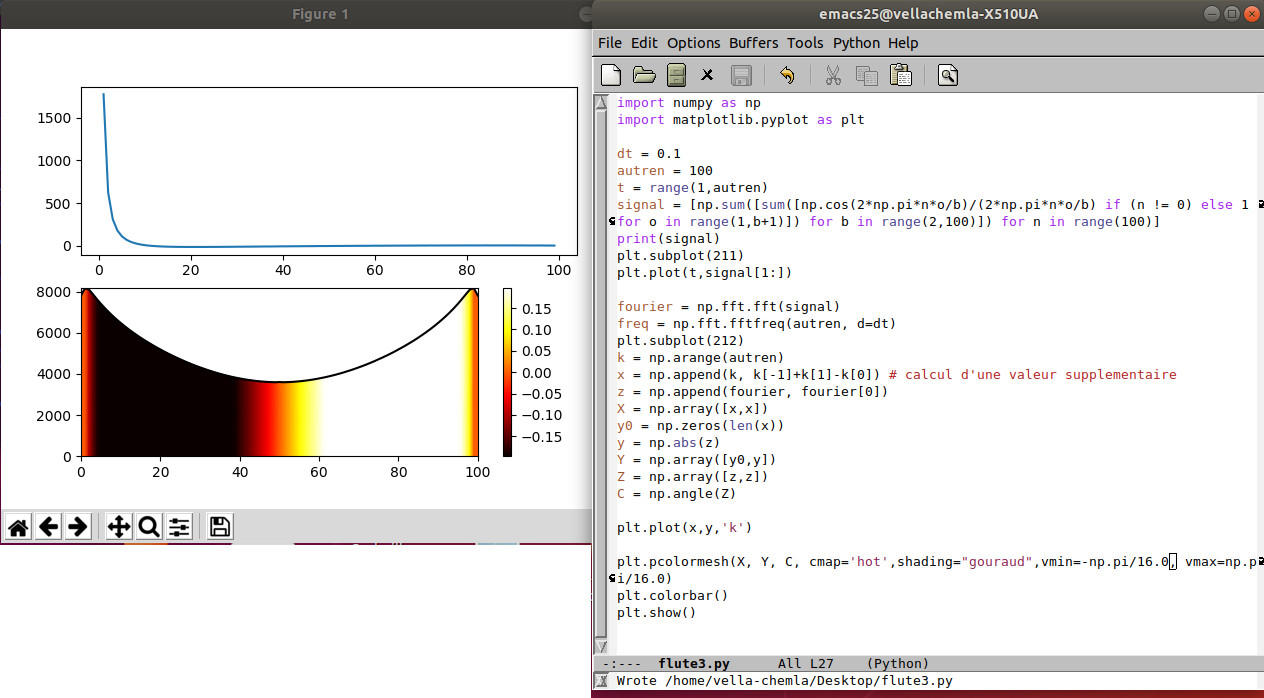 
-
2.5.2019 : Petits manèges des images du site (les autres sont en bas de la pages Notes) (557)








-
30.4.2019 : L’avenir des mathématiques (André Weil, 1947) (556)

-
♥ 29.4.2019 : compositions palindromiques (555)

-
26.4.2019 : Comme s’il en pleuvait (554)
   
-
25.4.2019 : entre deux (553)

-
22.4.2019 : picorer l’aléa (552)

-
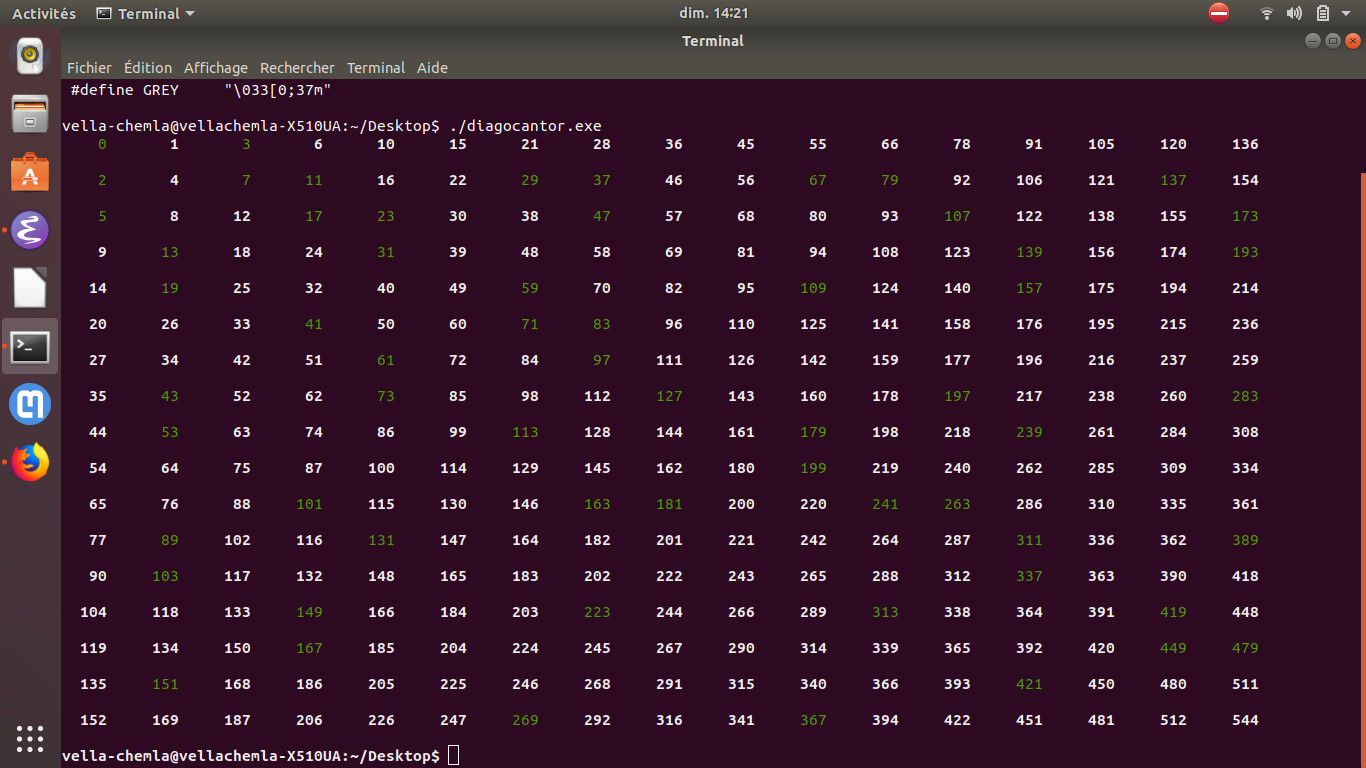
21.4.2019 : visualiser les premiers sur une numérotation ℕ2 → ℕ de Cantor ; on voit 3 colonnes sans premiers ! (551)

-
8.4.2019 : Guide-chant en python : il s’agissait de convertir les fréquences des notes de la gamme en une suite d’entiers successifs, à partir d’une note de base (ici Do=32.7) (550)
  avril 2025 avril 2025   propagation des ondes sonores, propagation de la chaleur propagation des ondes sonores, propagation de la chaleur 

-
28.3.2019 : Probabilités disjointes (549)

-
24.3.2019 : Mes gratitudes (je viens de lire le roman de Delphine Le Vigan) (548)

-
16.3.2019 : No need to ask, it’s a smooth operator (bis) (547)

-
17.3.2019 : probabilités stochastiques (546)

-
13.3.2019 : No need to ask, it’s a smooth operator (545)

-
12.3.2019 : une décomposition singulière en bonne forme (544)

-
10.3.2019 : une décomposition bien singulière ! (543)

-
7.3.2019 : tentative pour synthétiser l’information (décompositions en valeurs singulières) (542)

-
♥♥ 5.3.2019 : comment perçoit-on ? (titre : Spectre lumineux) où apparaît mystérieusement une fonction triangulaire (541)

-
4.3.2019 : transformée de Fourier de la fonction qui envoie les premiers sur eux-mêmes (la somme de somme de cosinus qui me plaît tant) (540)

-
3.3.2019 : 4 petits gifs pour faire appréhender l’aléa des décomposants de Goldbach (pgm python
 ) (539) ) (539)
n < 100 rapide  lent lent 
n >= 100 (de 100 à 3600 par pas de 100) rapide  lent lent 
-
16.2.2019 : Nombres et sphère quantique (538)

-
18.2.2019 : Probabilistiquement ou quantiquement (537) (ou il est question de polarisation)
 et les transparents de Grangier en référence, vers lesquels le lien sort bien sûr en erreur 404, à peine 6 ans après... et les transparents de Grangier en référence, vers lesquels le lien sort bien sûr en erreur 404, à peine 6 ans après... 
-
15.2.2019 : Théorème de Morley dans le corps des quaternions (536)

-
février 2019 : Une application de la démonstration d’Alain Connes du théorème de Morley, à ℤ/13ℤ (535), qui contient une racine cubique de l’unité
 . .
Programme Python pour preuve du théorème de Morley par Alain Connes à l’été 2020  Reprise par Jacques, article posté sur mon blog (15.2.2022) Reprise par Jacques, article posté sur mon blog (15.2.2022) 
-
13.2.2019 : la différence géométrique entre premiers et composés est que pour un polygone régulier d’un nombre premier p de côtés, il n’existe pas de rotation d’angle 2π/k pour k compris entre 3 et √p, autour du centre du polygone, qui laisse le polygone invariant. (534) (il faut que le nombre p soit supérieur ou égal à 7 pour que l’énoncé ci-dessus soit correct.)
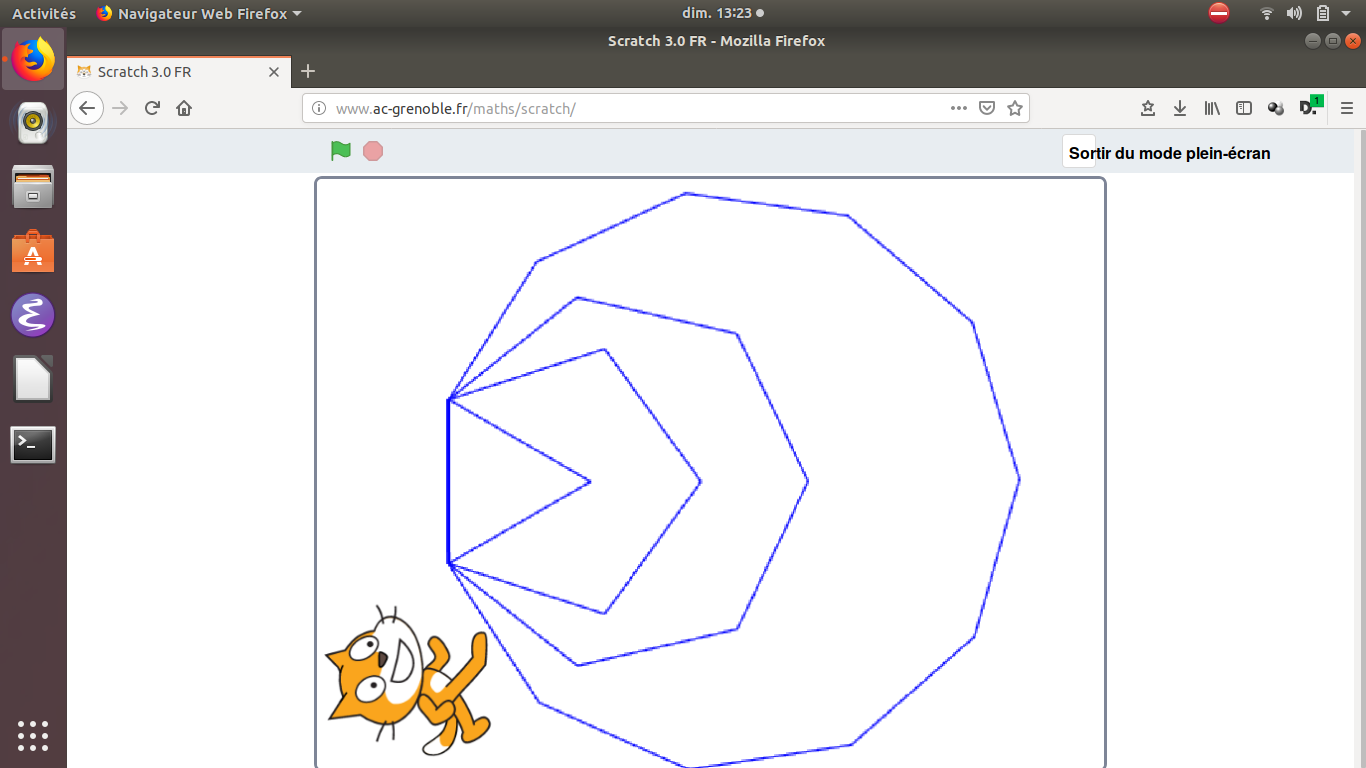
-
6.2.2019 : Représentation des nombres par des matrices du groupe affine (533)

-
28.1.2019 : Théorème de Morley dans ℤ/13ℤ (532)

-
26.1.2019 : où l’on retrouve ζ autrement (531)
 31.5.2019 : 31.5.2019 :  (en) (en)  23.7.2019 : annexe 23.7.2019 : annexe 
-
5.2.2019 : Divisions euclidiennes représentées par des matrices (530)

-
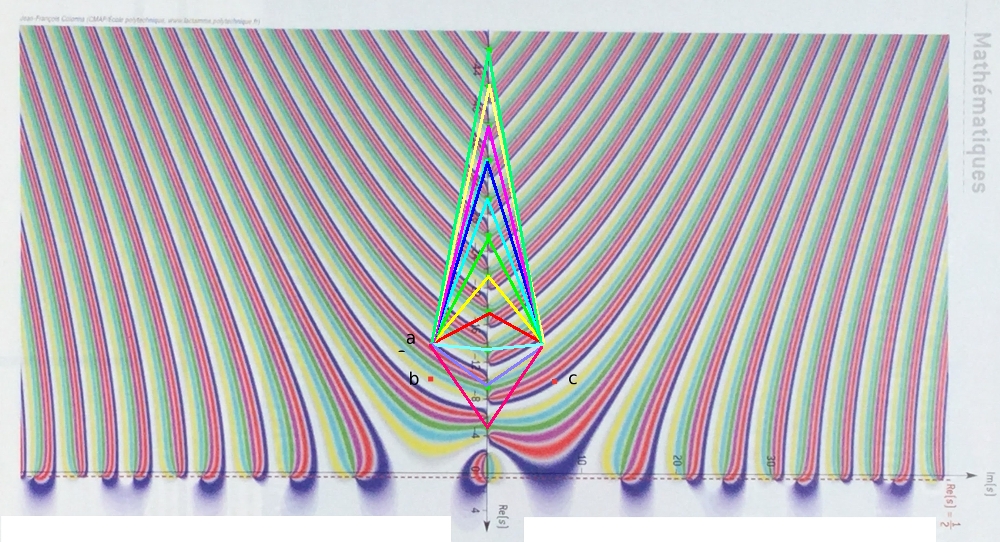
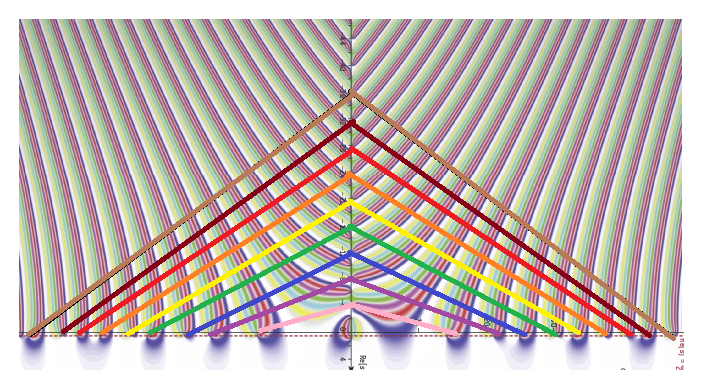
2.2.2019 : un jour, j’avais dessiné ça, je trouvais ça joli. Maintenant, j’aimerais savoir dessiner des triangles isocèles de sommets d’affixes complexes, isocèles en les zéros triviaux, et d’autres sommets les zéros non-triviaux et leur conjugué (un triangle isocèle a les affixes de ses sommets qui vérifient : a b+a b+c c = a c+ac+b b). (529)
-
19.1.2019 : motifs rythmiques (ou jouer aux dés) (528)

-
17.1.2019 : sauts quantiques ceci cela (527)

-
16.1.2019 : conjonctions de mots booléens
(526)

-
13.1.2019 : périodicité et palindromie dans les séquences booléennes (525)

-
9.1.2019 : formule du crible de Poincaré quand on élimine au maximum 2 classes de congruence sur p selon tout p premier(524)
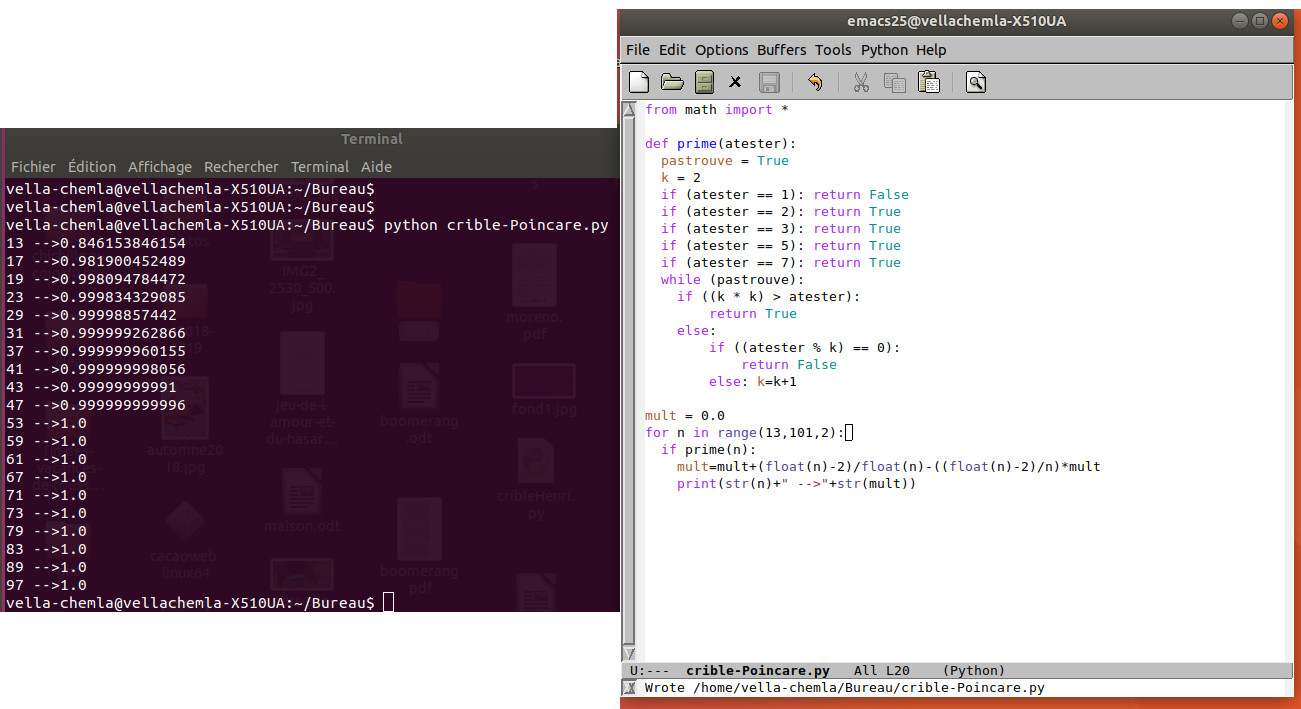
Rosser et Schoenfeld (Hadamard et La Vallée-Poussin)
 
-
9.1.2019 : ne garder que les premiers qui n’ont aucun reste commun avec n (523)

-
7.1.2019 : Mots périodiques ou comment projeter tous les restes sur 0 ou 1 (522)


-
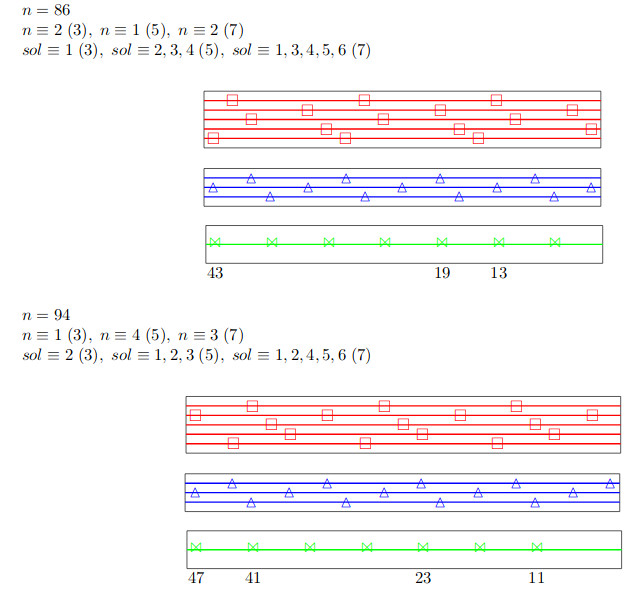
4.1.2019 : clef de Sol(utions), pavages du plan par des parallélogrammes (521)

-
3.1.2019 : maillage du tore par des polytopes dont les faces sont des parallélogrammes (520)

-
3.1.2019 : gâteau 3-frères (519)

-
2.1.2019 : Où sont les tores ? (518)

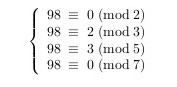   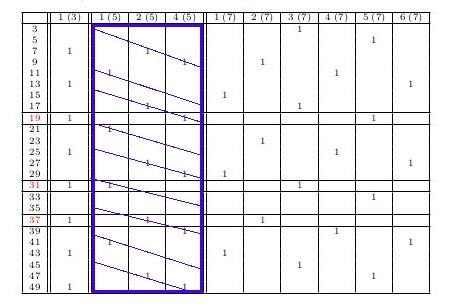 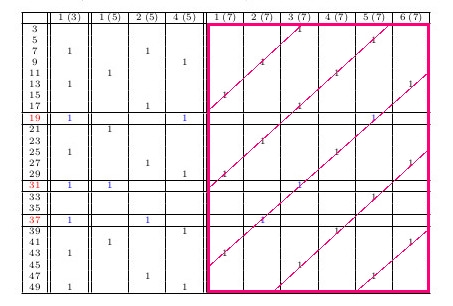  (ou des guirlandes de Noël à la topologie...)
(ou des guirlandes de Noël à la topologie...)
-
31.12.2018 : Dancing Links pour Conjecture de Goldbach, selon le Christmas tree de Donald Knuth (517)

 
traductions d’interviews        
-
26.12.2018 : programme de l’équation fonctionnelle vérifiée par ψ(x) qui est
2ψ(x)+1=(1/√x)*(2ψ(1/x)+1)   (jusqu’à 8, j’adore !) (516) (jusqu’à 8, j’adore !) (516)
Article de Jacobi en référence de l’équation fonctionnelle 
Référence à Siméon-Denis Poisson et définition de θ_4 
-
25.12.2018 : Essayer de calculer par programme les fonctions ψ(x) et ξ(t) de Riemann (515)

-
22.12.2018 : Essayer de comprendre la formule de Riemann (514)

-
9.12.2018 : Insister sur la somme de cosinus qui associe : (513)
- 0 aux nombres premiers,
- (pk-p)/(p-1) aux puissances pures de nombres premiers,
- une somme combinatoire aisée à calculer aux produits de nombres premiers simples
dont la factorisation ne contient pas au moins un carré
(ex : scd(2.3.5)=2+3+5+2.3+2.5+3.5)
- un produit récursif aisé à calculer aux nombres
dont la factorisation contient au moins un carré de premier
scd(pkx)=(p+1)scd(pk-1x)
 
-
5.12.2018 : pgcd et matrices (512)

-
3.12.2018 : Séparer (511)
-
2.12.2018 : Calculer pour tout entier n la somme des pgcd(n,k), k allant de 2 à n-1.
On voit bien les points alignés sur la droite y=x-2 pour les x qui sont des nombres premiers ! (510)
-
2.12.2018 : Somme des diviseurs par formule de récurrence (de Chazy ?). (509)
On voit bien les points alignés sur la droite y=x+1 pour les x qui sont des nombres premiers !
-
2.12.2018 : Coder le vrai par -1 (somme de booléens divise=-1, ne divise pas = 1) (508)

On voit bien les points alignés sur la droite (la plus haute) y=x+1 pour les x qui sont des nombres premiers !
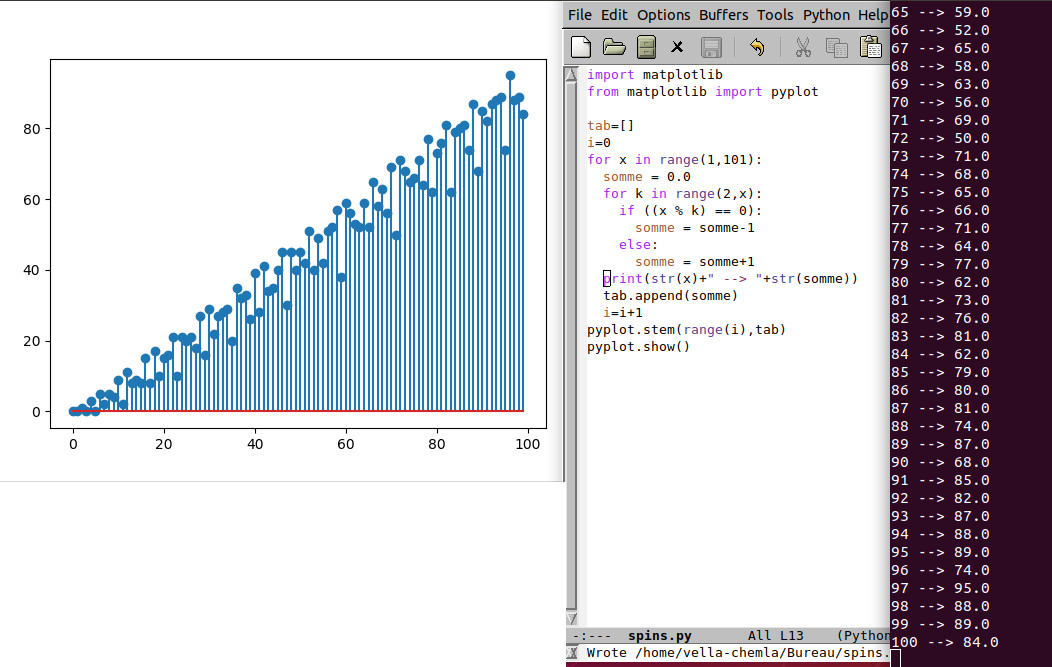 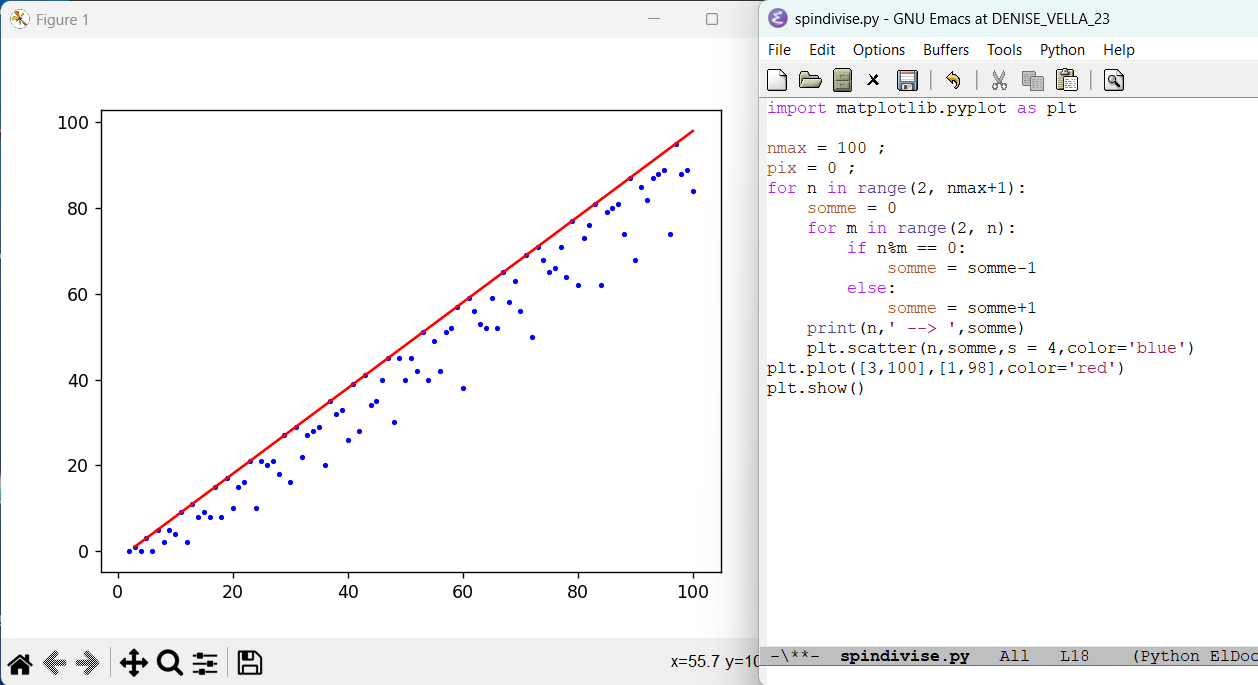
Explication de Jacques : 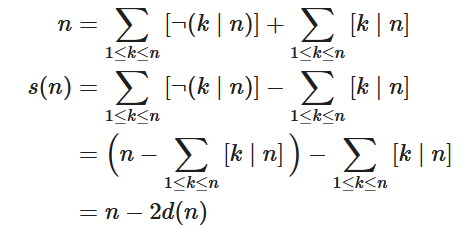
-
30.11.2018 : triplets Goldbachiques (507)

-
6.11.2018 : différence de logarithmes intégrals (506)
 
-
4.11.2018 : une somme alternée de cosinus tout à fait surprenante (505)

-
4.11.2018 : écarts entre deux nombres premiers consécutifs : distribution (504)
jusqu’à 10000  jusqu’à 100000 jusqu’à 100000  jusqu’à 1000000 jusqu’à 1000000 
-
28.10.2018 : alterner (503)


-
14.10.2018 : Arêtes (502)

-
13.10.2018 : multiplier les dendrites (501)
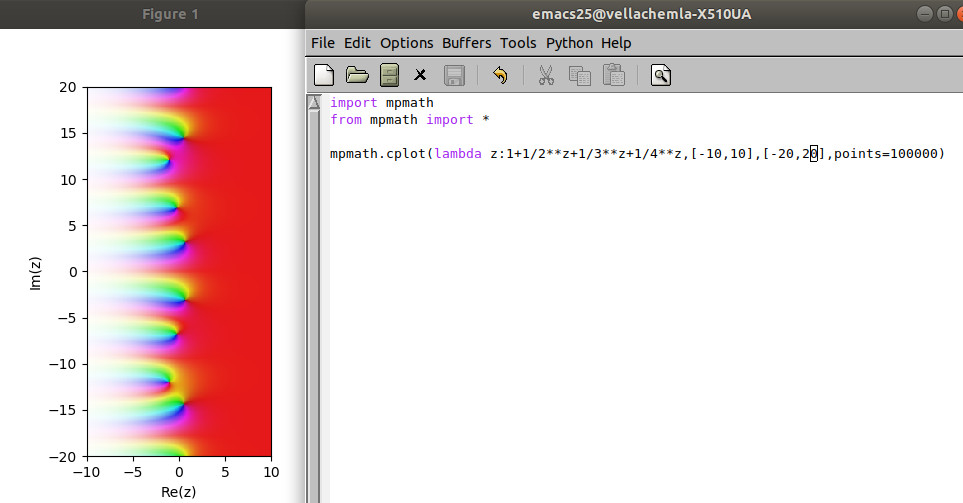 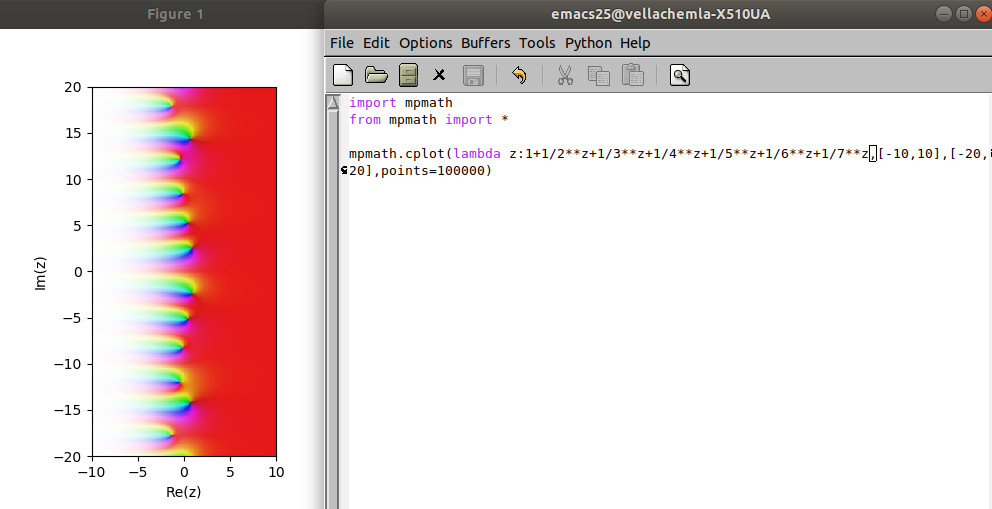
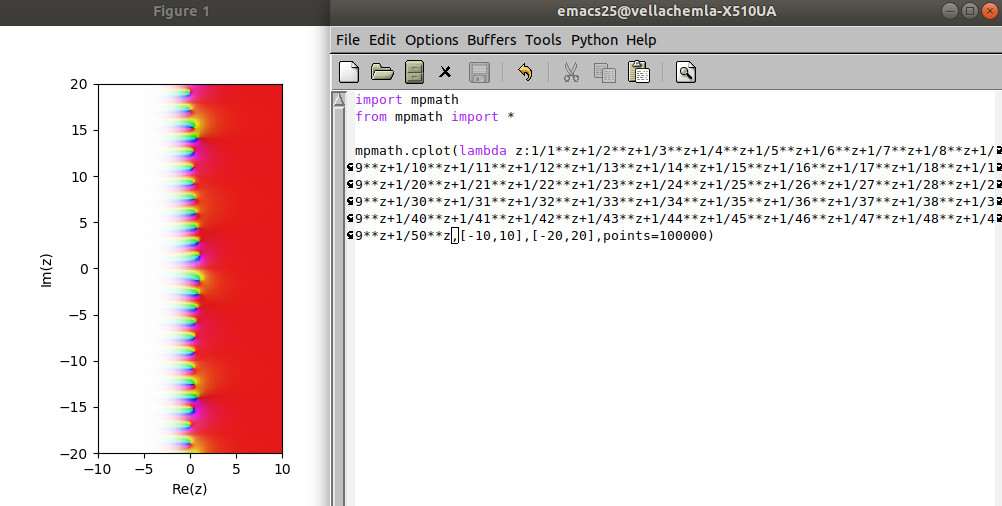 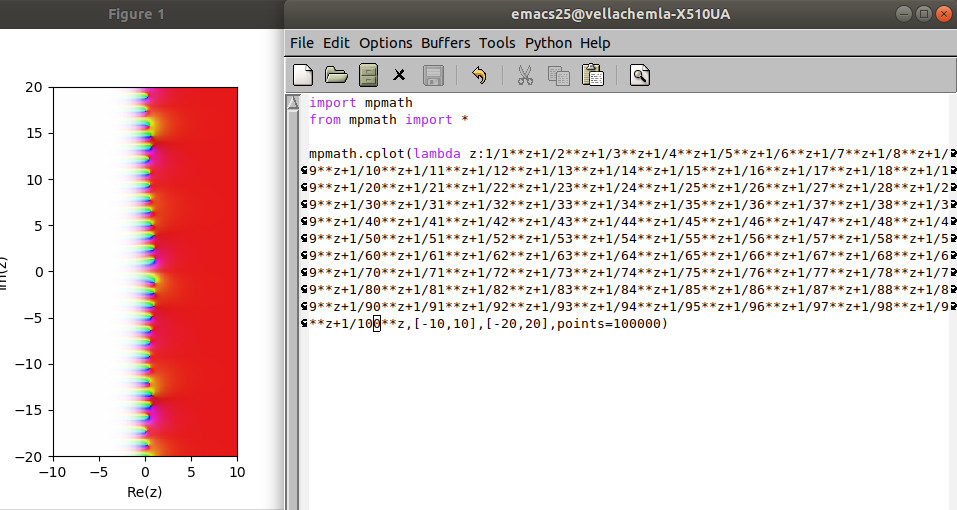
-
6.10.2018 : On réalise par programme qu’on peut remplacer le signe de l’intégrale définissant li(x) par un signe somme. (500)
Explication : la différence entre la somme et l’intégrale est contrôlée car la dérivée de 1/log(x), qui est -1/(xlog(x)2), est intégrable.
Il faudrait du coup réussir à comprendre pourquoi Σde y=2 à x 1/ln y permet de compter π(x) le nombre de nombres premiers inférieurs ou égaux à x.
La somme des inverses des logarithmes népériens vaut par exemple 78627 pour 106 quand π(x) vaut 78498.
Elle vaut 664918 pour 107 quand π(x) vaut 664579.  
-
6.10.2018 : Danses serpentines (499)

-
29.9.2018 : Arbres et chip-firing, that’s fun ! (498)

-
25.9.2018 : Sommes des lignes d’une matrice et nombres premiers (497)

-
19.9.2018 : Une fonction de comptage des nombres premiers (496)
  ainsi qu’une fonction plus simple, jusqu’à la racine ainsi qu’une fonction plus simple, jusqu’à la racine   fourvoiement complet dans cette seconde version : j’ajoute 1 sur les premiers et 0 sur les autres en prenant le floor d’un nombre entre 0 et 1, dur ! fourvoiement complet dans cette seconde version : j’ajoute 1 sur les premiers et 0 sur les autres en prenant le floor d’un nombre entre 0 et 1, dur !
-
19.9.2018 : Compter les nombres composés (495)

-
2.9.2018 : Peau de tambour (494)

-
1.9.2018 : Vers 1/2 (493)

-
30.8.2018 : petit dessin comme ça (492)

-
28.8.2018 : quantifier les nombres premiers (491)
 (en) (en) 
-
27.8.2018 : décomposants de Goldbach sur planche de Galton (490)
 (en) (en) 
-
25.8.2018 : un nombre p > 4 est premier si (p-1)!/p n’est pas un entier. On imagine la courbe dans le plan d’une fonction, qui grimpe à toute vitesse (f(6)=120, f(8)=6720, f(9)=40320, ...), cette courbe ne croise pas la trame reliant les points de coordonnées entières quand l’abscisse d’un point est un nombre premier alors qu’elle le fait lorsque l’abscisse est un nombre composé (ces factorielles me trottent dans la tête depuis mai 2006) (489)
 Des courbes qui grimpent trop vite Des courbes qui grimpent trop vite 
Rappel :
- un nombre premier apparaît à l’exposant 1 dans la factorisation de sa propre factorielle ;
- un nombre premier ne divise pas la factorielle de l’entier qui le précède,
le quotient (p-1)!/p n’est jamais entier
(à relier au théorème de Wilson) ;
- un nombre composé apparaît au moins au carré dans la factorisation de sa propre factorielle ;
- un nombre composé divise la factorielle de l’entier qui le précède.
-
20.8.2018 : Conjecture de Goldbach, chip-firing game, matrices 2x2 et descente infinie (488)



-
19.8.2018 : Conjecture de Goldbach et chip-firing games (487)

-
18.8.2018 : Hyperboloïde à une nappe (486)

-
17.8.2018 : Memo pour les puissances 10ièmes (485)

-
14.8.2018 : L’été, revenir à des calculs simples (484)

-
9.8.2018 : Souvenir : SNURPF, exemple (483)

-
9.8.2018 : Par hasard ? (482)

-
7.8.2018 : Deviendrons-nous tous des produits ? (481)

-
On constate par programme jusqu’à 106 qu’il existe toujours une décomposition de Goldbach p+q de n un nombre pair non double de premier pour laquelle on trouve r nombre premier avec p2+r=0 dans ℤ/nℤ. (480)
-
1.8.2018 : Vouloir connaître leurs structures (479)
 
-
28.7.2018 : Nouvelle idée (478)

-
21.7.2018 : solde de tout compte (477)

-
♥ 12.7.2018 : palindromes (476)


-
1.7.2018 : Faire ses comptes (475)
 (en) (en) 
-
30.6.2018 : Proposition de démonstration de la conjecture de Goldbach (474)
 (en) (en) 
-
29.6.2018 : Croît (473)

-
29.6.2018 : Préciser (472)

-
24.6.2018 : Errer (471)

-
23.6.2018 : Je dois corriger encore plus : un bête petit d qui se transforme en a et c’est la catastrophe. (470)

-
23.6.2018 : Je dois corriger : en fait, la note ne fait que démontrer le fait suivant, peut-être ; si un ensemble de nombres vérifient la conjecture, alors vérifient également la conjecture les doubles de ces nombres, et du coup, les doubles de leur double, et les doubles des doubles de leur double, etc. (469)
On sait que Goldbach est vraie pour tous les pairs jusqu’à 4.1018 (test sur ordinateur d’Oliveira e Silva en 2014), appelons l’un d’entre eux n, je crois avoir démontré que CG est vraie pour tout 2k n.
Suite au prochain épisode, j’espère, mais ça me paraît peu probable car autant par le passage d’un nombre simple à son double, ce qui est pratique, c’est que les petits et les grands sommants des décompositions de Goldbach du nombre simple devenant tous des petits sommants des décompositions du nombre double, on arrive à avoir des relations entre les nombres de décompositions, autant lorsqu’on prend un multiple du simple par k (ou p premier idéalement, ça doit être plus judicieux), je ne sais pas si on peut obtenir de telles relations.
-
3.6.2018 : petites expérimentations autour de ζ (468)



-
2.6.2019 : Conjecture de Goldbach et les impairs (467)
 
-
2.6.2018 : sommes de cosinus, polynômes de Tchebychev, annulation de polynômes sur le disque-unité complexe...
(466)

-
29.5.2018 : d’où viennent les idées ? (465)

-
12.5.2018 : des hauts et des bas (464)
 (en) (en) 
-
12.5.2018 : Comprendre ce que l’on n’avait pas compris (463)

-
8.5.2018 : hier, Alain Connes m’a envoyé un petit texte qui explique où il a l’impression que mon raisonnement pêche. (462)
Je pense que si on a toujours Xd(n)-Xa(n) = n/4-π(n) et qu’à partir d’un certain rang Xd(n) > n/4-π(n), alors Xa(n) sera toujours supérieur ou égal à 1 à partir du rang en question. L’exercice subsidiaire visait à fournir une explication intuitive du fait qu’à partir d’un certain rang, Xd(n) > n/4-π(n).

Programme python correspondant au petit texte et son résultat


Comme on peut le constater, bien que de différence quasi-constante,
Xa(n) et Xd(n) subissent de sacrées variations d’un pair au suivant.
Un jeu d’images pour étayer les réflexions

-
26.4.2018 : Quel ordre ? (correction de calculs)
(461)

-
7.4.2018 : Article factice généré avec Mathgen (460)

-
7.4.2018 : Des tours et des détours (459)

-
2.4.2018 : Aujourd’hui, j’ai découvert une (presque-on-m-a-dit-)égalité qui m’épate, elle est peut-être déjà connue : (458)
e((-ln 3)/2) ≈ γ.
où γ est la constante d’Euler-Mascheroni

-
1.4.2018 : Couleur (457)

-
18.3.2018 : Nombres orthogonaux (456)

-
17.3.2018 : Différences de nombres orthogonaux (455)

-
9.3.2018 : Moyenne des parties fractionnaires des parties réelles des zéros de zêta (454)

-
7.3.2018 : Fonctions en dents-de-scie (453)

-
2.3.2018 : Courbe de Hilbert en python-Logo (452)
 mars 2024 : pour Olivier, la traduction par Google de l’article de Hilbert présentant sa courbe
mars 2024 : pour Olivier, la traduction par Google de l’article de Hilbert présentant sa courbe 
-
25.2.2018 : Faire le point (451)
 avril 2025 : prolonger un peu cela avril 2025 : prolonger un peu cela 
 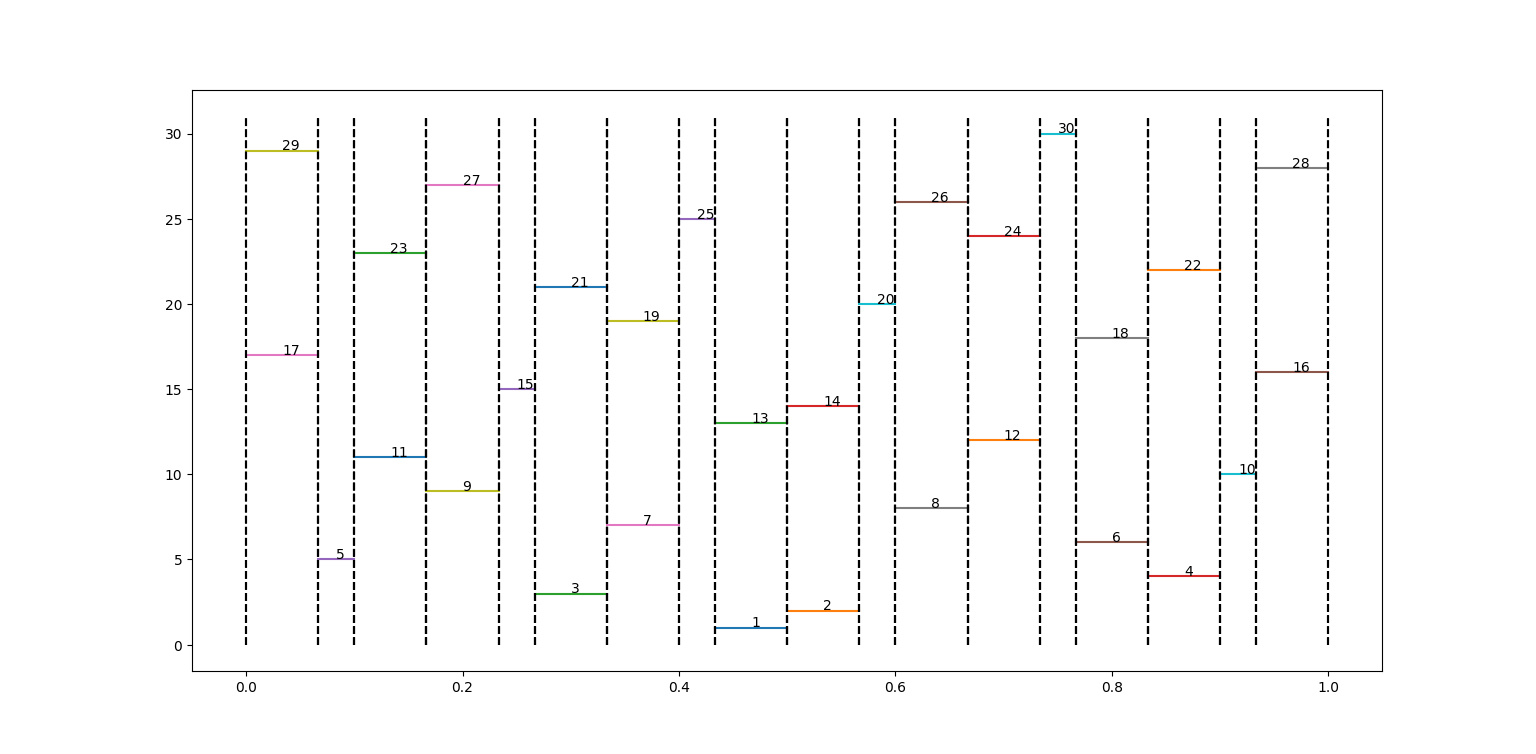 
-
21.2.2018 : Littéralement (450)

-
3.1.2018 : Cantique des nombres premiers (449)

-
2.1.2018 : Pollen (448)

-
2.1.2018 : Moins surprenant le 2 janvier que le jour du nouvel an (447)

-
26.12.2017 : Tout juste réalisé ; 2 et 5 partagent une propriété, ils sont les deux seuls nombres tels que tout autre nombre ayant même dernier chiffre qu’eux est composé. (446)
-
24.12.2017 : Recherches arithmétiques de Gauss, sections 121, 122 et 123.
 ![]()
-
23.12.2017 : tentative d’explication des conjectures (445)

-
20.12.2017 : Conjectures : (444)
- un nombre n qui se termine par 1
est un nombre premier ou une puissance d’un nombre premier
si et seulement si
l’équation modulaire x10 = 1 (mod n) a exactement 10 solutions.
- un nombre n qui se termine par 3, 7 ou 9
est un nombre premier ou une puissance d’un nombre premier
si et seulement si
l’équation modulaire x10 = 1 (mod n) a exactement 2 solutions.
-
18.12.2017 : Nombre de solutions de l’équation x^5=1 (mod n) avec n de dernier chiffre 1. (443)


-
16.12.2017 : Lien entre le nombre de racines quatrièmes de 1 modulo n et
le nombre de nombres premiers de la factorisation de n impair de chaque type (4k+1 ou 4k+3). (442)

-
15.12.2017 : Compter les racines quatrièmes de 1 (441)

-
5.12.2017 : Compter les racines de 1 modulo n pour trouver le nombre de nombres premiers de la factorisation de n, un nombre impair. (440)
 correction correction 

Dans ℤ/nℤ, n impair, 1 a 2k racines carrées, avec k le nombre de nombres premiers différents intervenant dans la factorisation de n.
-
3.12.2017 : j’avais mal énoncé la conjecture que voici, et on m’en a donné la démonstration : "le nombre de solutions de l’équation x2=x (mod n), pour n impair est égal à 2^k avec k le nombre de facteurs premiers de la décomposition de n." (439)





-
♥♥ 29.11.2017 : à chaque primorielle, le nombre de points fixes augmente d’une puissance de 2. (438)

-
29.11.2017 : Carrés fixes, carrés nuls (437)



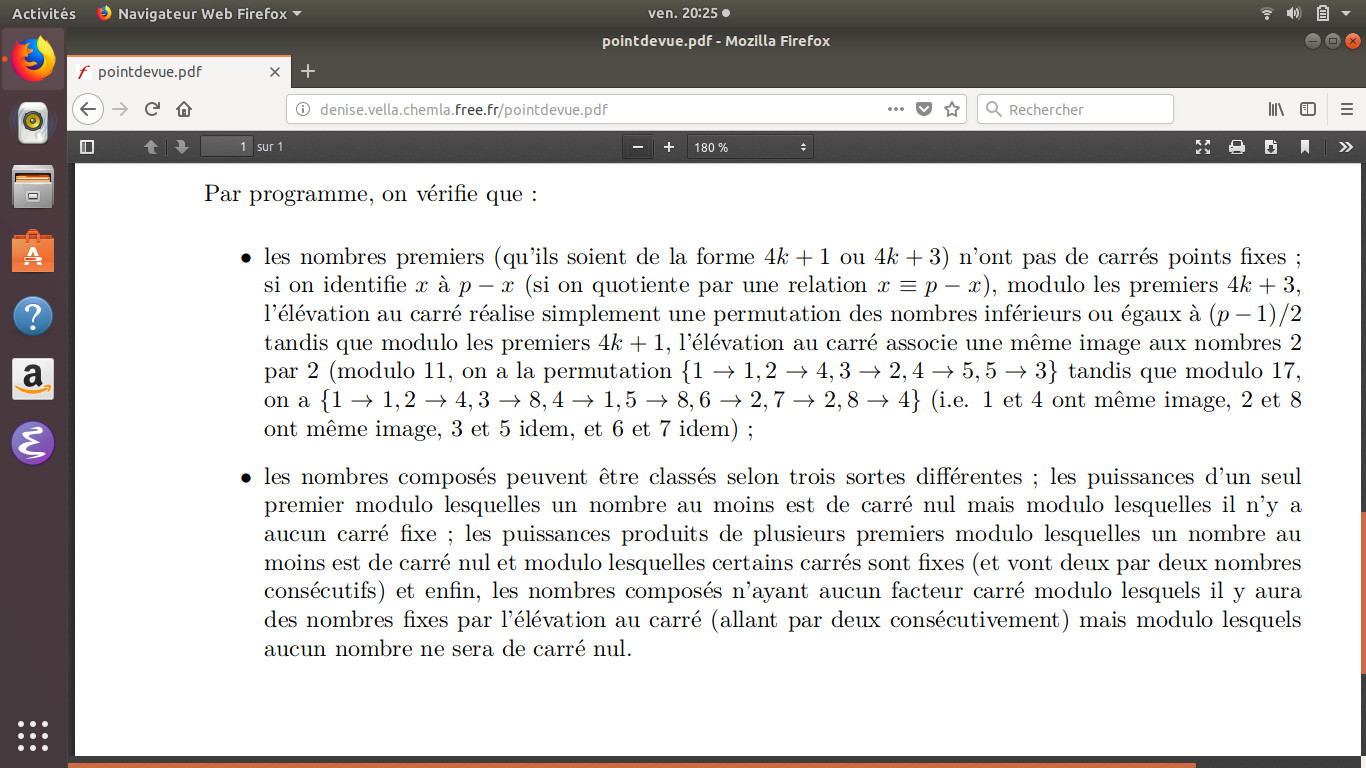 
-
25.11.2017 : Diagrammes (436)

-
22.11.2017 : Tautologies (435)

-
16.11.2017 : Motifs rythmiques (434)


-
10.11.2017 : alignements dans la table "est un résidu quadratique de" (les nombres premiers, c’est connu, maximise le nombre de résidus quadratiques, i.e. correspondent à des lignes horizontales à forte densité de points) (433)
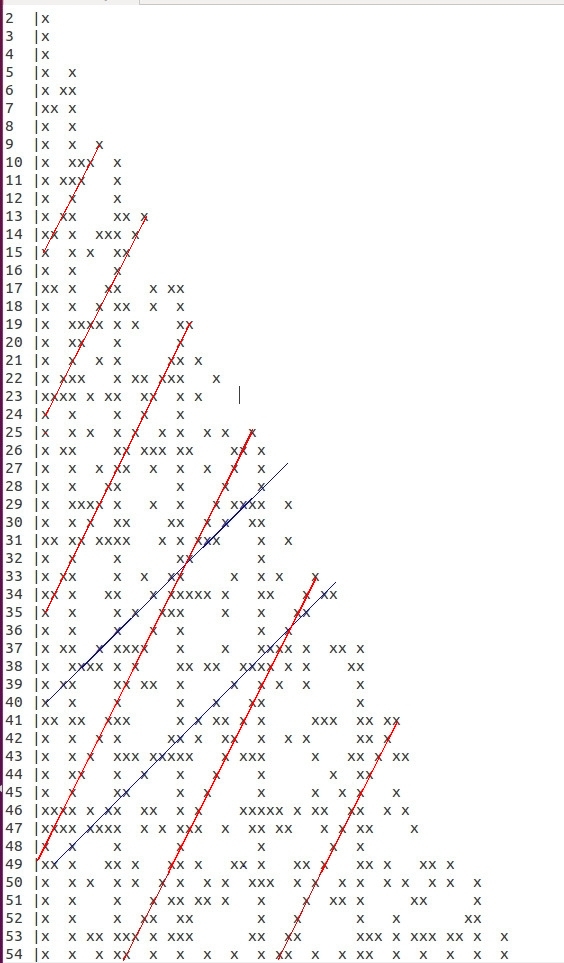  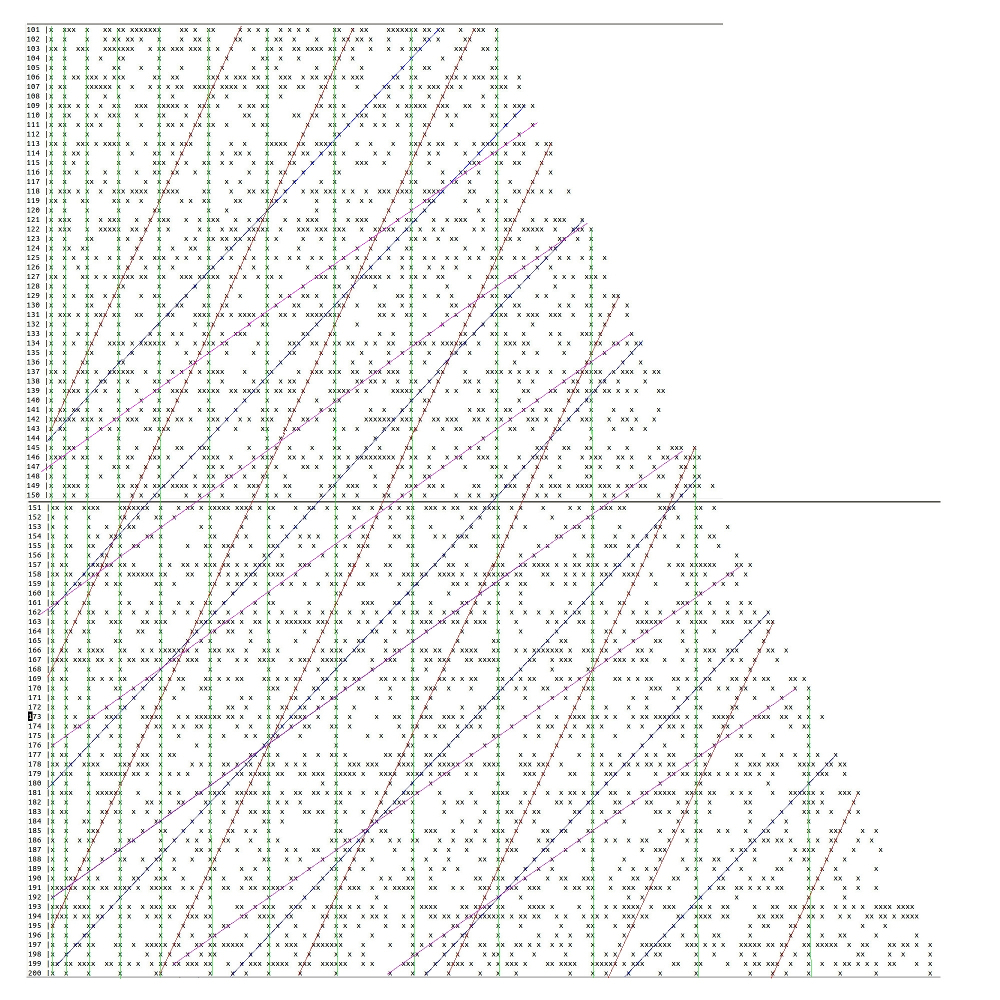
-
9.11.2017 : Tiens, c’est marrant ! (432)
  Il suffisait d’aller jusqu’à 100 000 Il suffisait d’aller jusqu’à 100 000   
-
8.11.2017 : la table "est un résidu quadratique de" de Gauss (apériodicité qui engendre de la périodicité) (431)

-
6.11.2017 : Racines de -1 et primalité (430)

-
5.11.2017 : Causer ou ne pas causer (429)

-
2.11.2017 : Simplicité : compter les produits valant -1. (428)
φ(n) nombres sont solutions de l’équation xy=-1

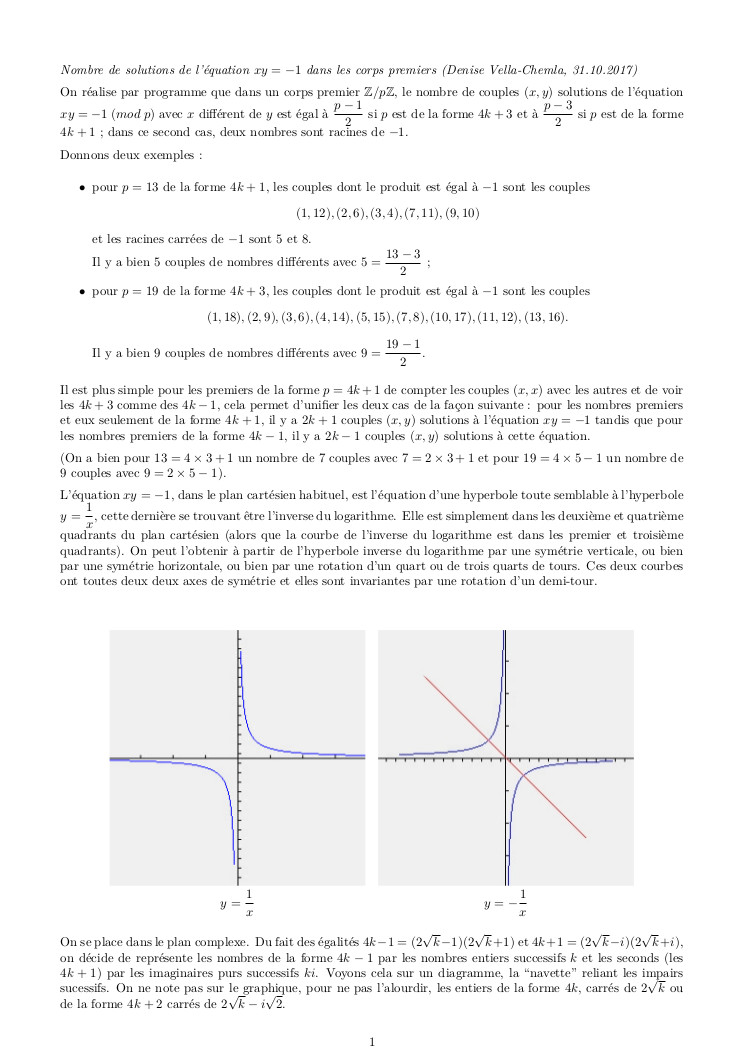 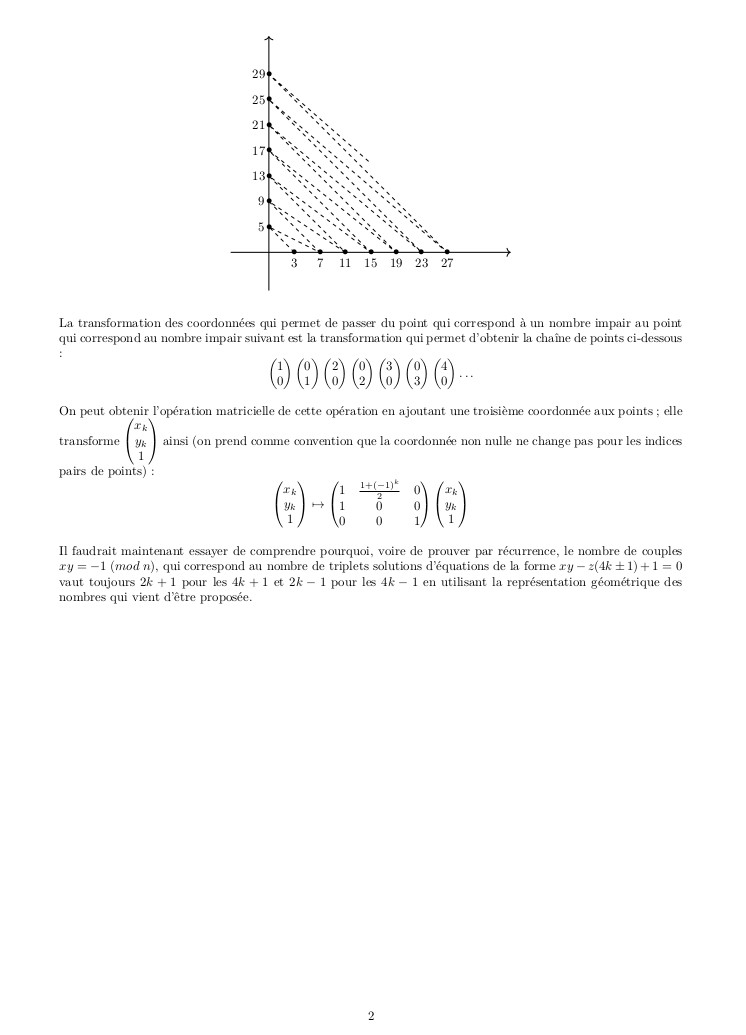
-
29.10.2017 : simplifier le guide-chant (427)
 avril 2025 avril 2025   
-
27.10.2017 : Calcul matriciel pour somme de diviseurs (426)

 
-
27.10.2017 : Spirale infernale (425)
 
-
17.10.2017 : Pile la moitié ! (424)
 
    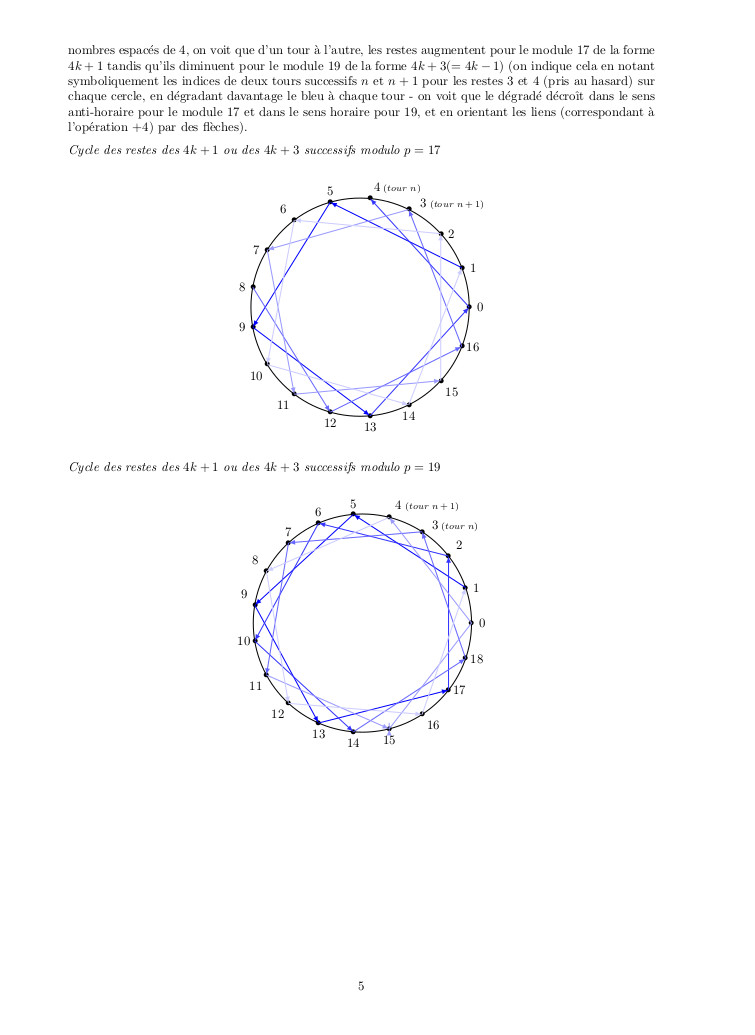 
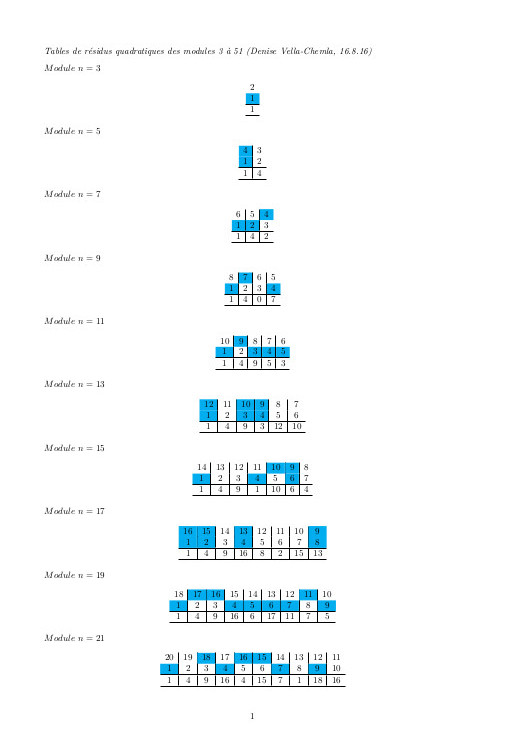 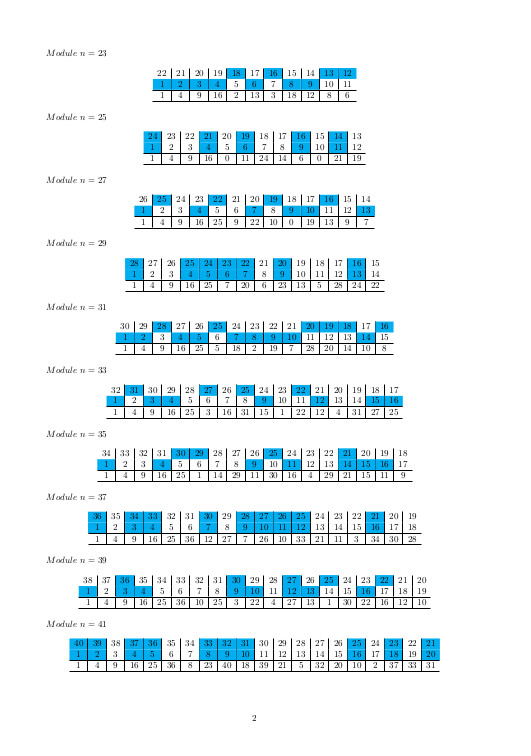 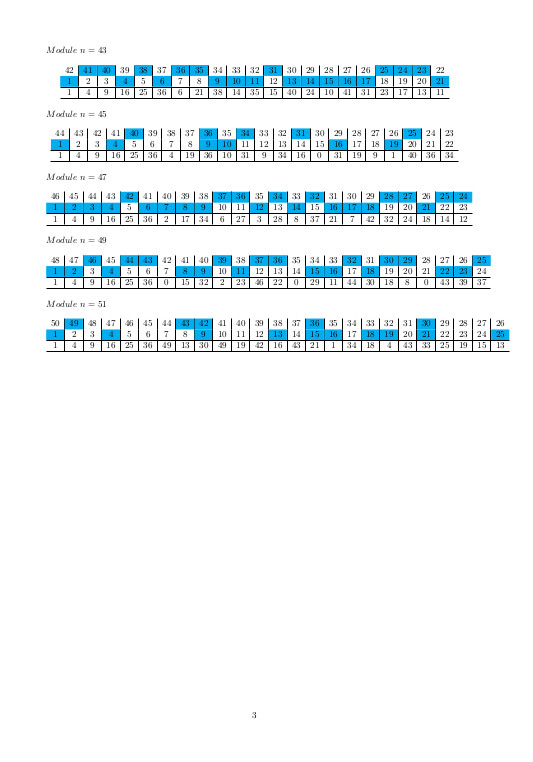
-
19.10.2017 : Continuer à chercher la trace d’un opérateur (423)

-
22.8.2017 : Moyennes des résidus quadratiques et moitiés des nombres (422)

-
22.8.2017 : Différence entre les fonctions f et F de l’article de Riemann (421)

-
17.8.2017 : Sommes de résidus modulaires (420)
  
-
12.8.2017 : géométrie modulaire et quantique (419)

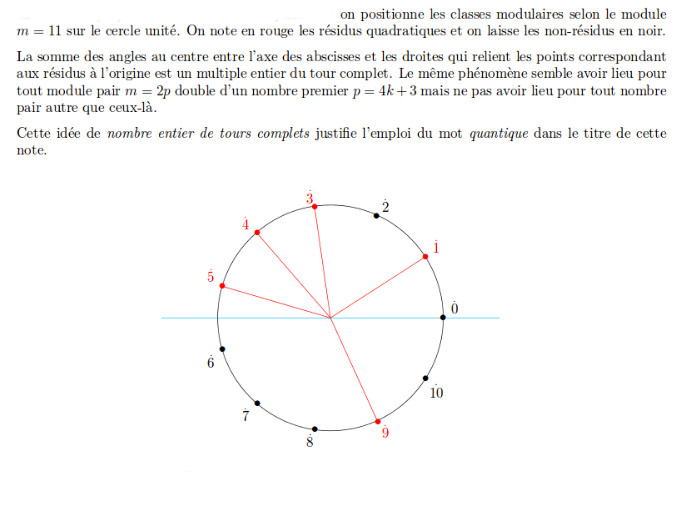
-
12.8.2017 : Valuations p-adiques dans les factorielles (418)


-
11.8.2017 : Transcription en Latex de wikisources d’Evariste Galois (417)


 

-
7.8.2017 : Spirale (416)

-
15.7.2017 : je crois que du fait que Zêta s’appuie sur Gamma, il faut chercher pour comprendre Zêta du côté de la divisibilité des factorielles (Gamma est l’extension de la factorielle au plan complexe). J’ai lu dans la Théorie des nombres de Lucas un théorème intéressant sur la divisibilité des factorielles. Pour trouver l’exposant de 7 dans la factorielle de 10000, il divise itérativement 10000 par 7 et il ajoute les quotients. Cela a comme conséquence qu’un nombre premier p apparaît à puissance de 1 dans la factorisation de sa factorielle (ainsi que dans les factorisations des nombres de p inclus à 2p exclus), les premiers plus petits que lui peuvent apparaître à puissance plus grande. Cette propriété mise au jour par Lucas fournit une fonction qui permet de distinguer les nombres premiers des nombres composés (associer au nombre sa factorielle, puis trouver sa propre valuation p-adique dans le nombre obtenu) ; les nombres premiers sont les seuls antécédents de 1 par cette fonction. (415)
-
13.7.2017 : Divisibilité des factorielles (Lucas) (414)

-
13.7.2017 : Preuve de Victor Varin du Keldysh Institute de Moscou que la somme de cosinus s’annule pour les premiers et uniquement eux (la somme de cosinus calcule la somme des diviseurs et la somme de diviseurs d’un nombre premier p vaut p+1). (413)

-
12.7.2017 : Vue de mes yeux vue : elle, c’est simple, je l’adore ! (412)
Pour sûr, elle part à l’infini, mais à chaque fois qu’elle redescend sur terre, c’est pour indiquer un nombre premier...
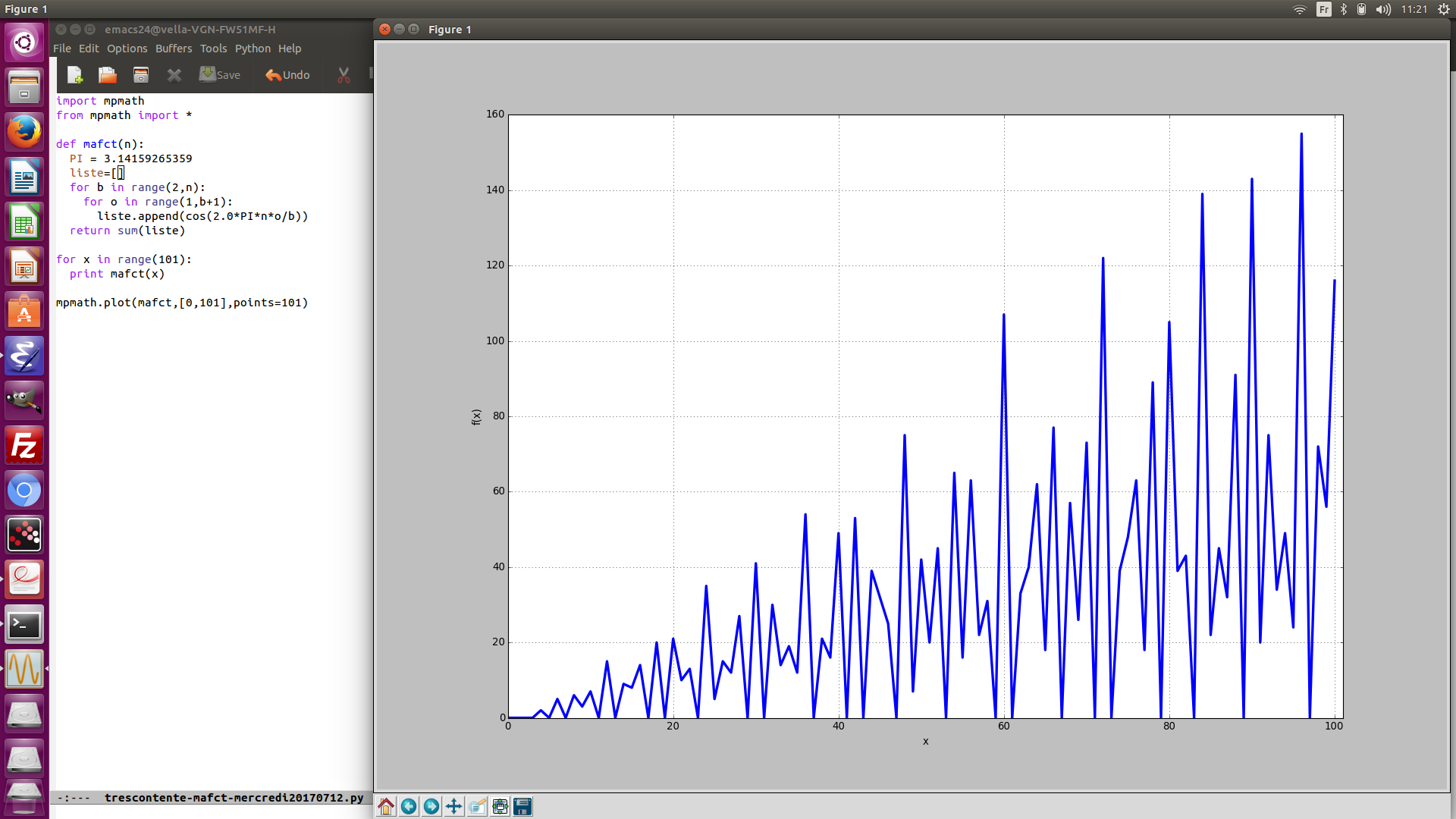
-
11.7.2017 : memo (411)

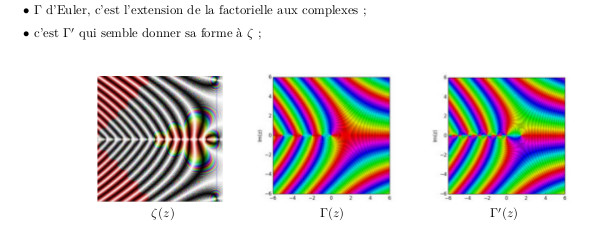
-
8.7.2017 : Programmer les fonctions de l’article de Riemann (correction dans la formule principale de Riemann : +ln 2 en -ln 2+πi) (410)

 Emerveillement (raccarreepourpi.pdf)
Emerveillement (raccarreepourpi.pdf) 
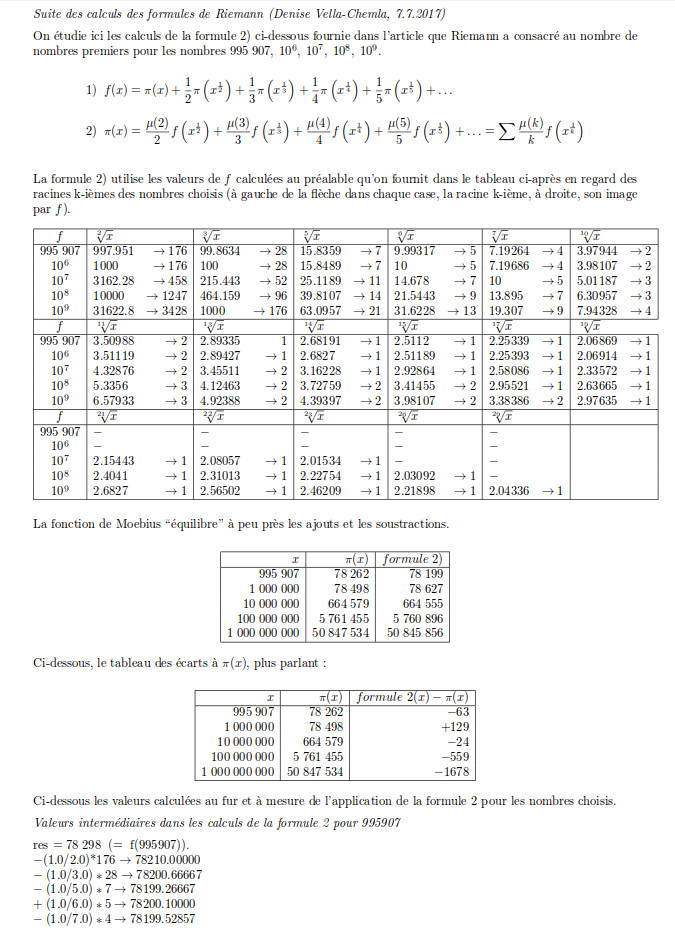 
-
7.7.2017 : se détendre (409)


-
2.7.2017 : Représentations colorées des fonctions Id, Li(z) (ou logarithme intégral Li(z)=li(z)-li(2) avec li(2)=1.4516378011749) et z/ln(z) dans le plan complexe : (408)
fonction Identité (Id)
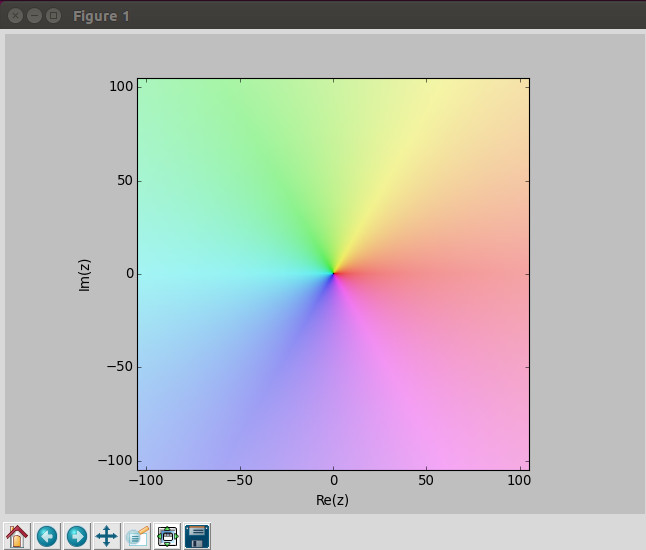 fonction logarithme intégral (Li(z))
fonction logarithme intégral (Li(z))
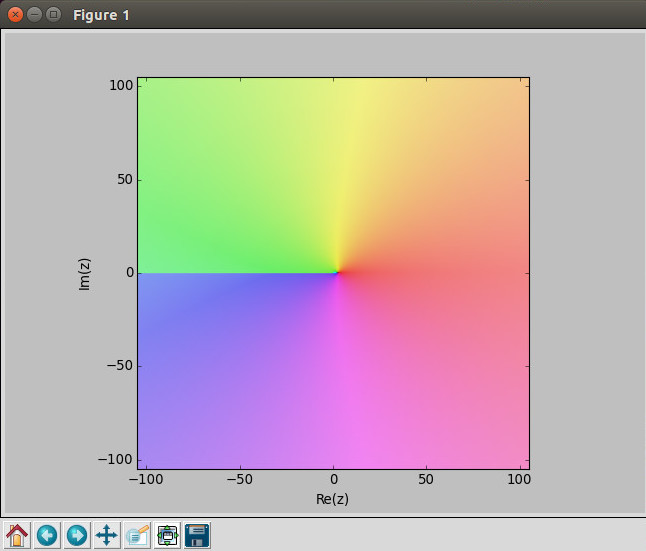 fonction logarithme intégral (Li(r))
fonction logarithme intégral (Li(r))
 fermeture-éclair
fermeture-éclair
 fonction z/ln(z)
fonction z/ln(z)
 fonction 7^z
fonction 7^z
 fonction 7^z-1
fonction 7^z-1
 fonction Li(z) (ici)
fonction Li(z) (ici)
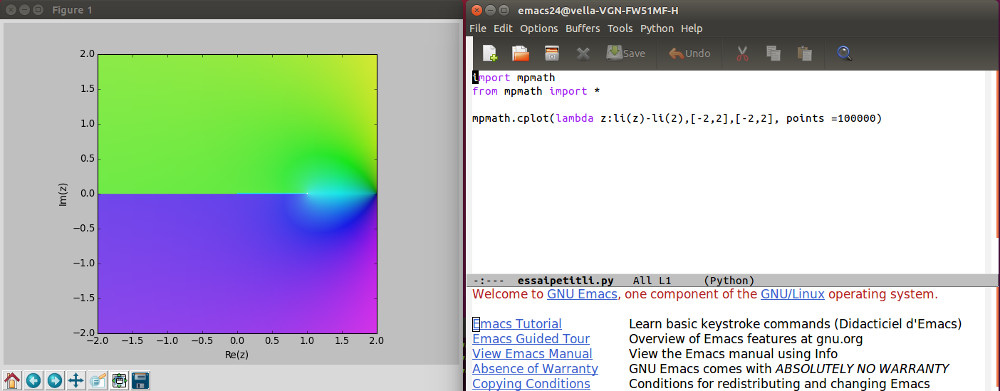 fonction Li(z) (là) fonction Li(z) (là)
 fonction Li(z) (ou bien là)
fonction Li(z) (ou bien là)
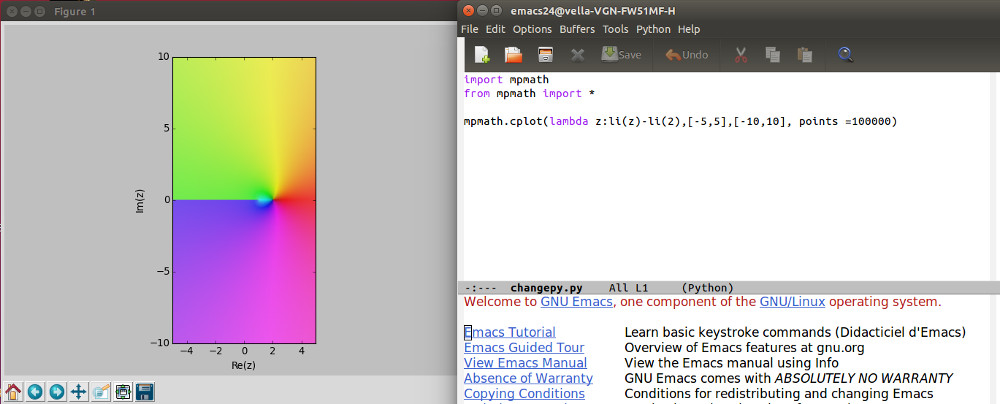 fonction √(z) fonction √(z)
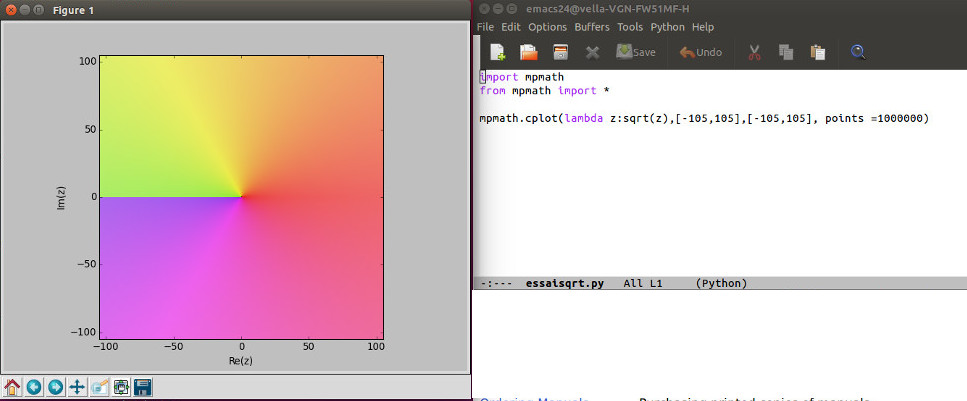 fonction cos(z) fonction cos(z)
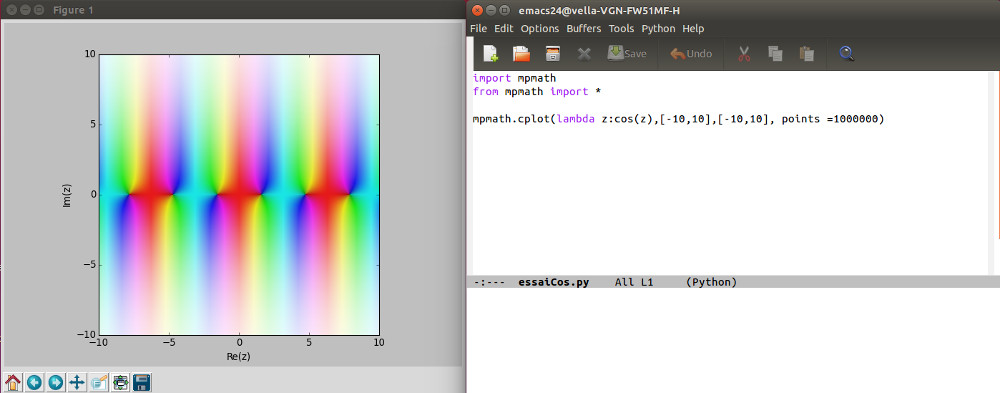
-
26.6.2017 : Calculer, à nouveau, des différences, ici entre deux parties imaginaires de deux zéros successifs de zêta, puis faire des statistiques (histogrammes) : on a réalisé, en observant ces différences, que certaines d’entre elles apparaissaient plus souvent, à un epsilon près. On ne conserve, en toute fin de listing (p.1563 et 4 pages suivantes) que les différences qui, à 10^{-5} près, apparaissent plus de 100 fois sur 100000 zéros. (407)

 (On s’est ramené à des entiers en multipliant tout par 10^5 et en tronquant les décimales (en prenant la partie entière)).
(On s’est ramené à des entiers en multipliant tout par 10^5 et en tronquant les décimales (en prenant la partie entière)).
-
25.6.2017 : Je sais que ça ne correspond à rien, mais c’est joli, quand même, non ? (406)
-
24.6.2017 : transcription de l’article de Riemann "Sur le nombre de nombres premiers inférieurs à une grandeur donnée" (405)
 
-
22.6.2017 : constantes (404)

-
20.6.2017 : atan, attends ou à temps. (403)

-
18.6.2017 : les nombres pairs doubles de nombres premiers ont un nombre impair de décomposants de Goldbach tandis que les nombres pairs doubles de nombres composés en ont un nombre pair. (402)
-
11.6.2017 : carré (401)

-
10.6.2017 : refaire ses gammes (400)

-
5.6.2017 : les points de l’espace de Goldbach commutent-ils ? (399)

 
-
1.6.2017 : mon but était de voir si, en introduisant un peu d’alea dans un pavage de Penrose, je n’aurais pas pu trouver un pavage identique à celui que j’ai utilisé dans ma tentative de démonstration de CG mais le problème est que je n’arrive pas à faire en sorte que les contraintes locales se propagent au pavage dans sa globalité (triangles nord-est tous de même couleur le long des diagonales et triangles sud-ouest tous de même couleur verticalement). (398)
 
-
31.5.2017 : Je n’arrive pas encore à trouver comment faire se propager les contraintes locales sur les couleurs. (397)
 Programme de pavage en asymptote
Programme de pavage en asymptote
-
27.5.2017 : vers un pavage de Penrose (396)

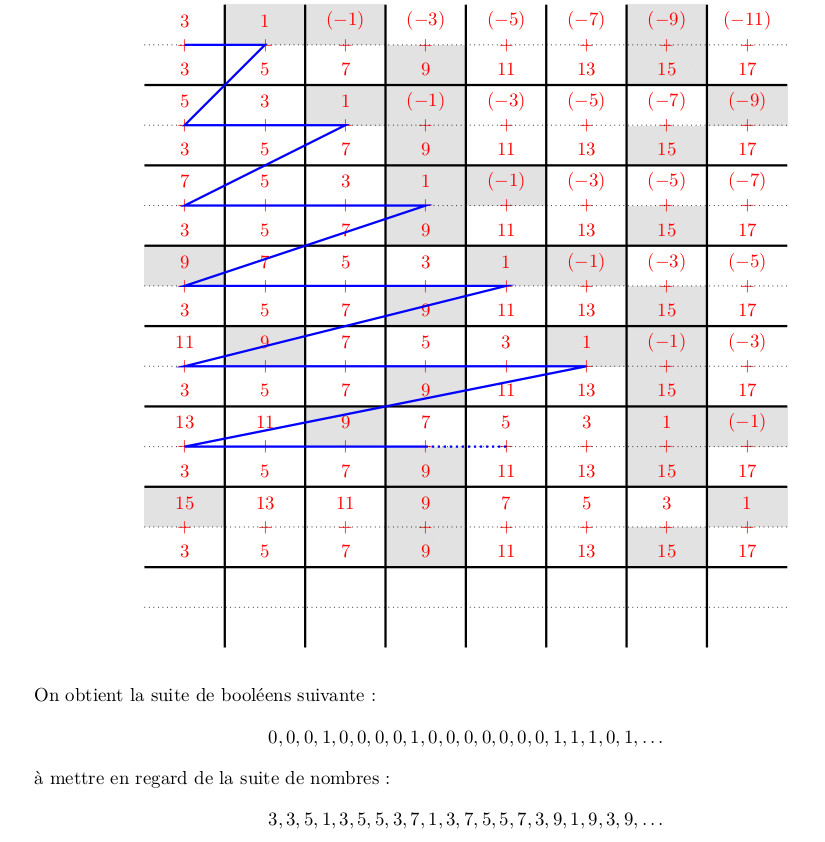 
-
24.5.2017 : rappel en image de la zone de comptage pour CG (395)

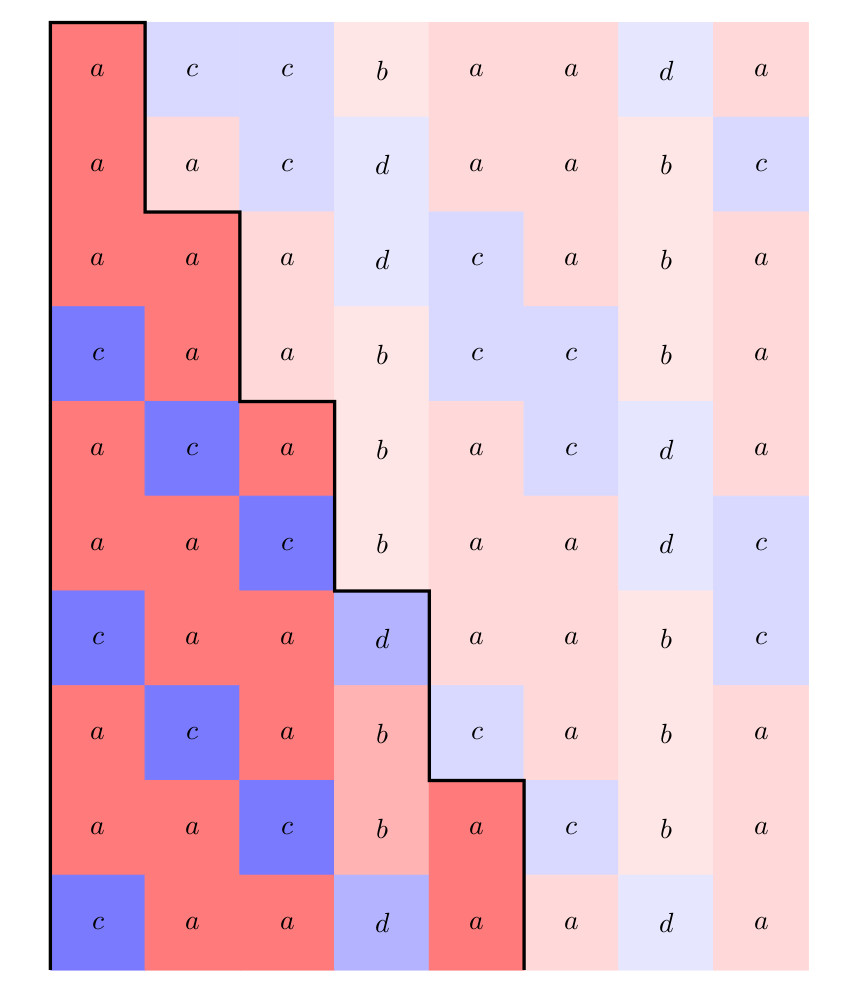
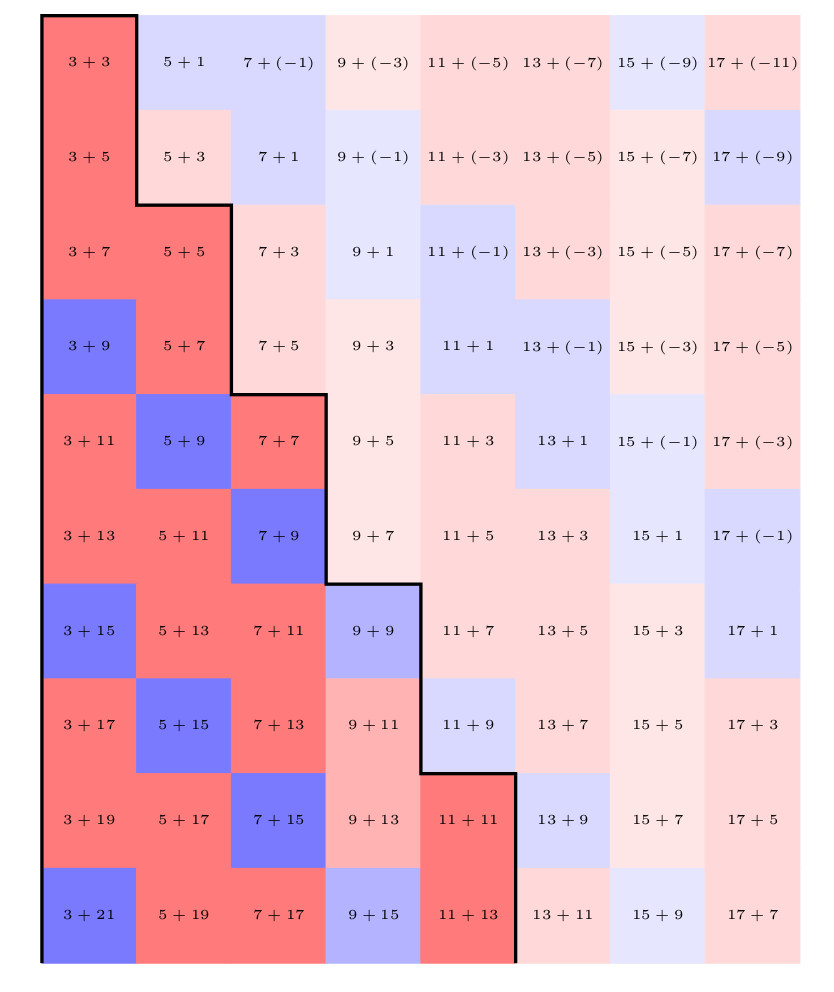
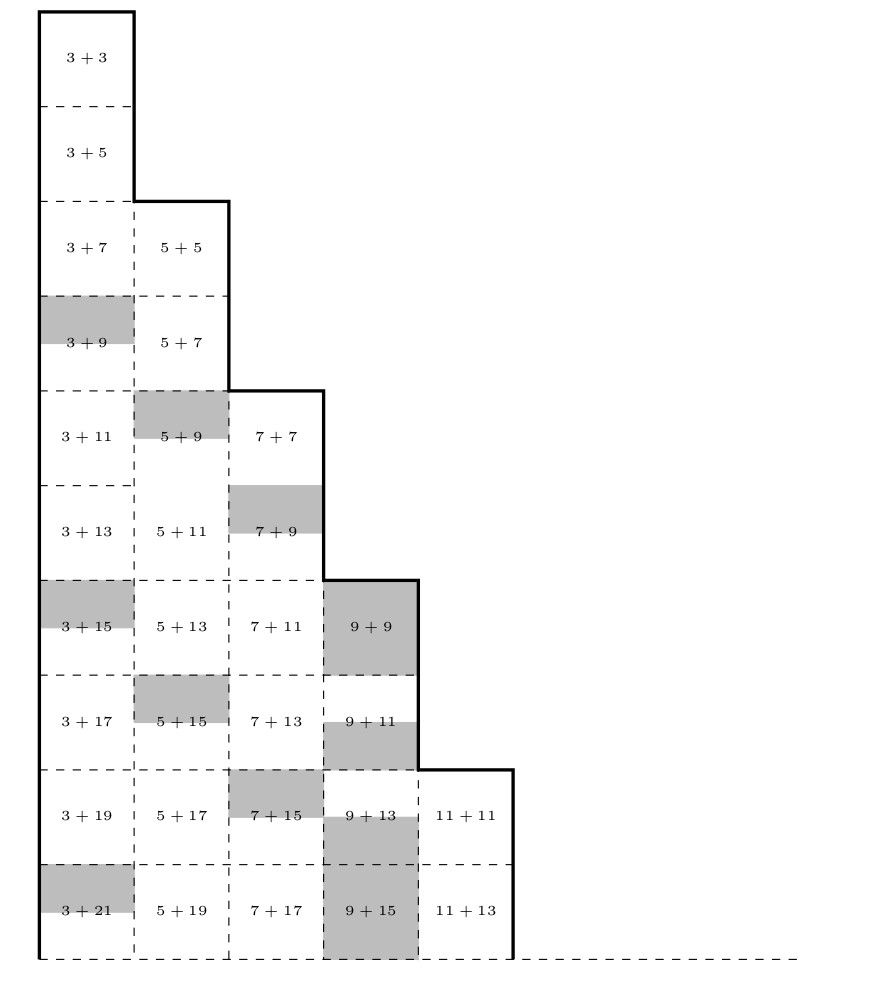

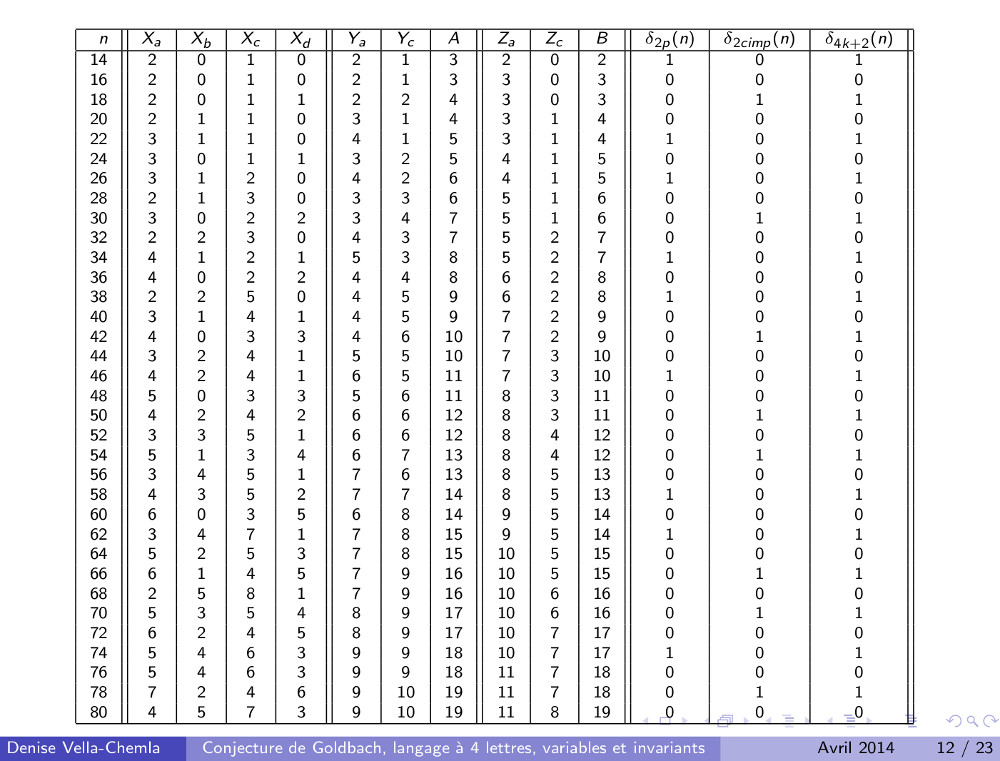
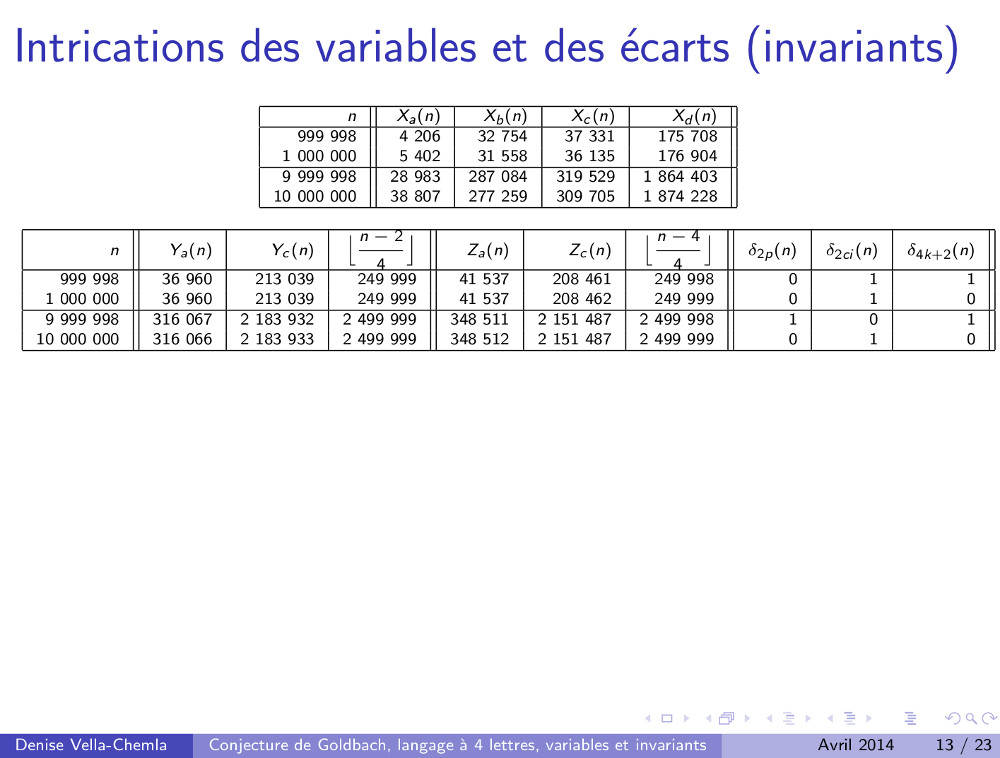


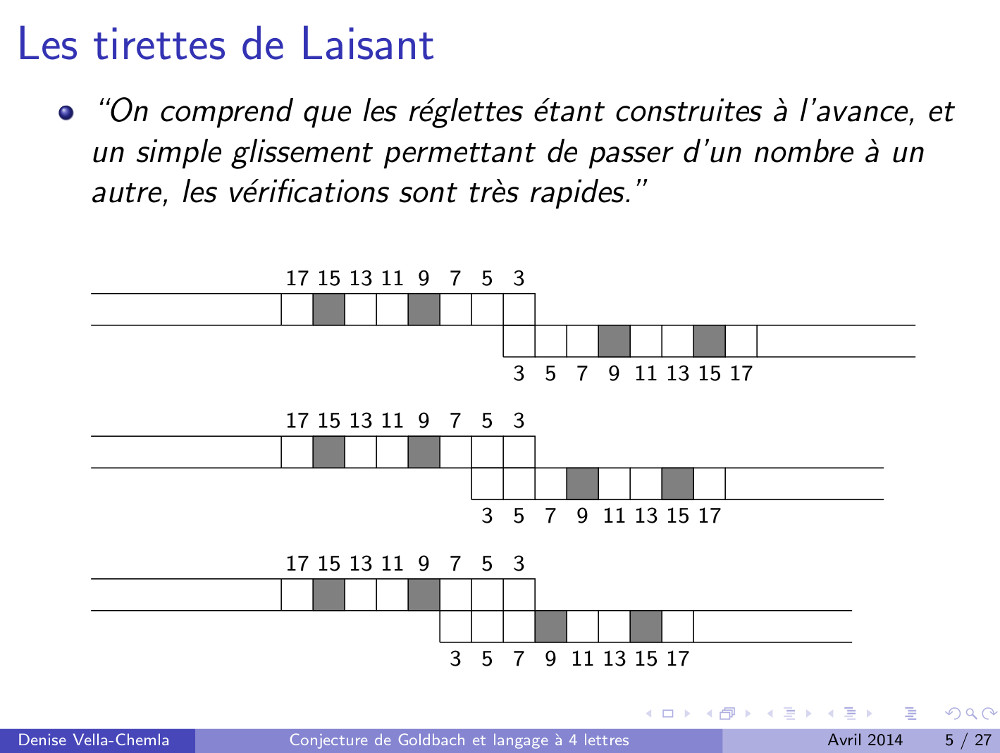
-
23.5.2017 : tuiles contenant des rectangles (doubles carrés) (394)

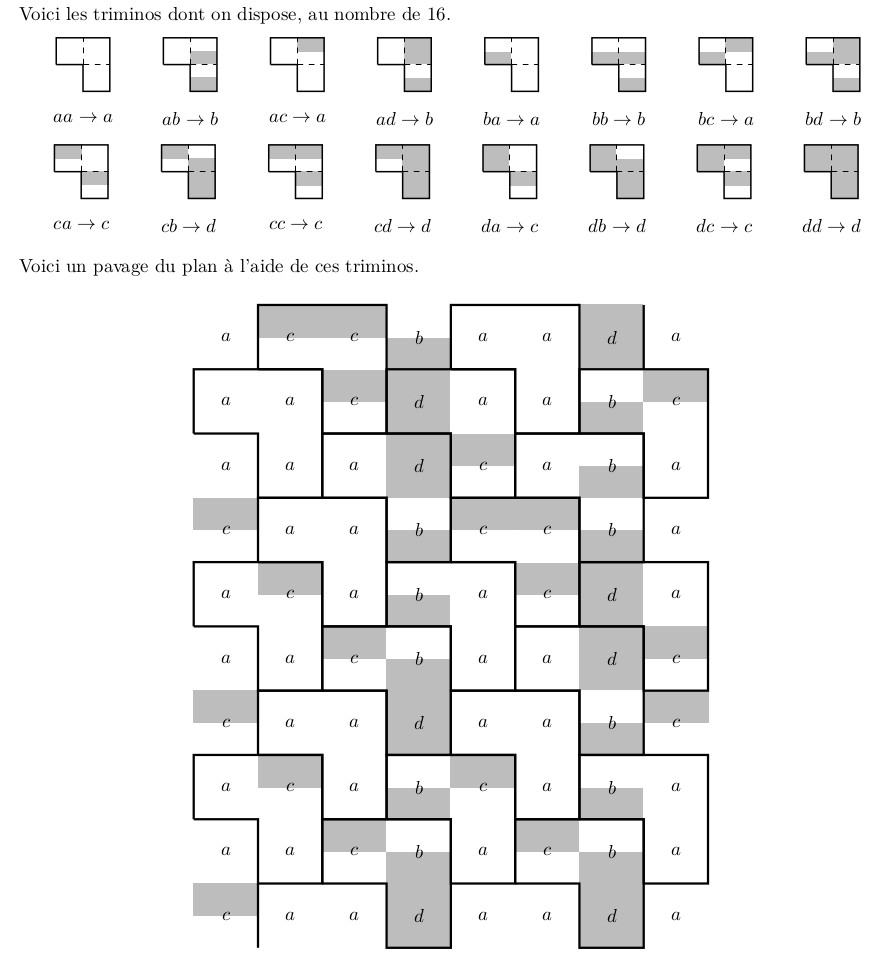
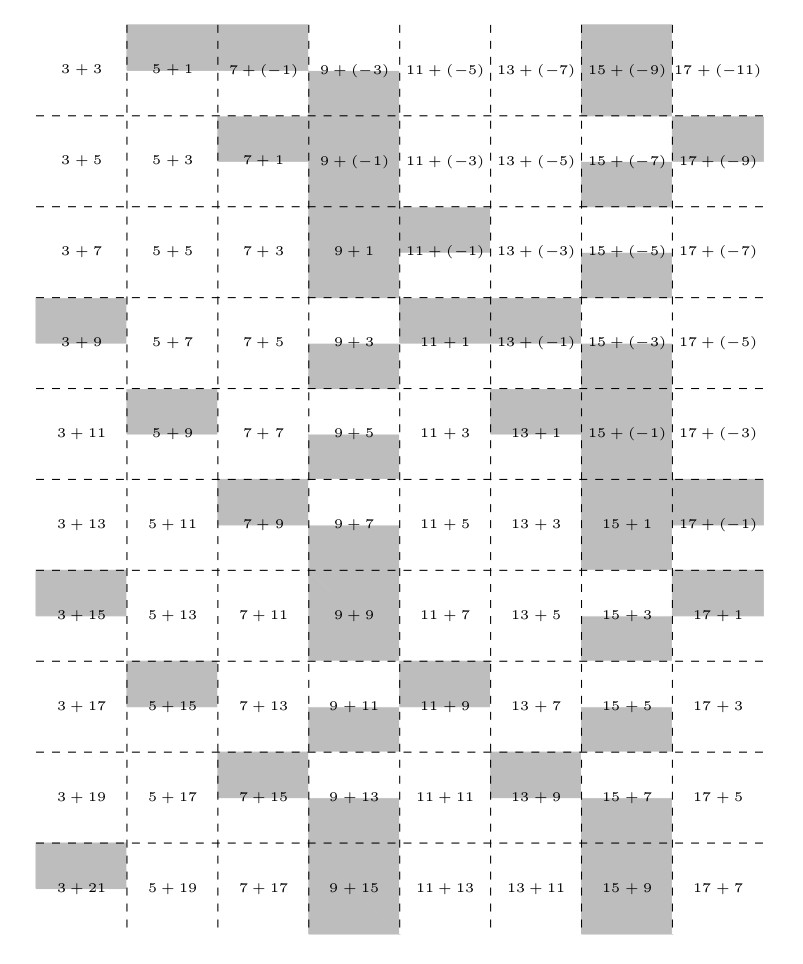
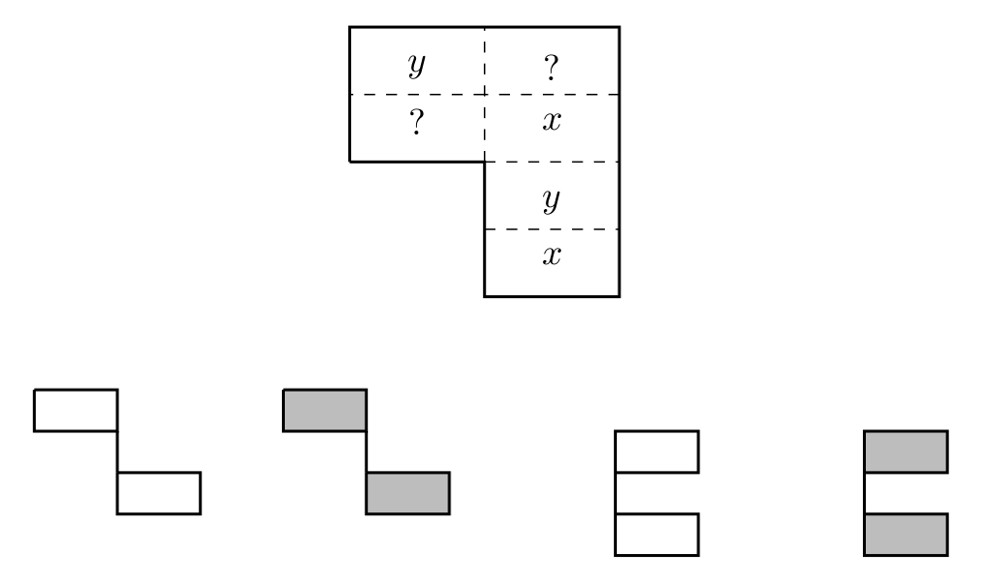
-
22.5.2017 : tuiles contenant des triangles isocèles bicolores (393)

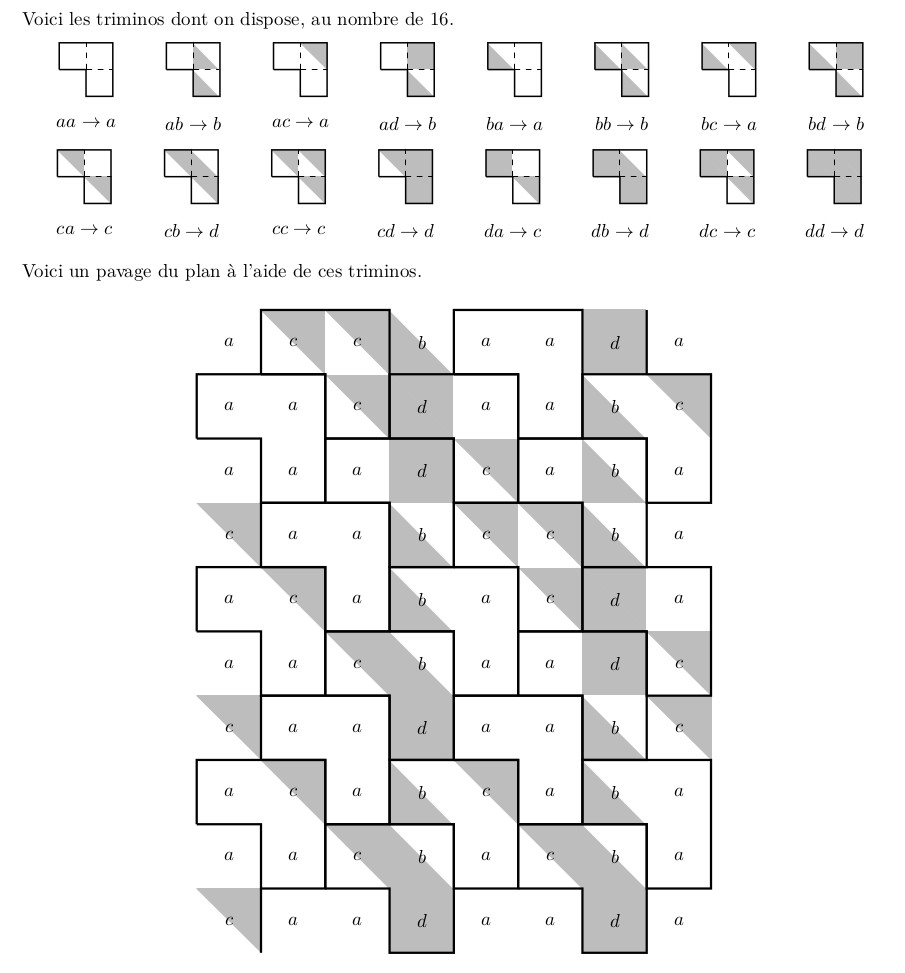

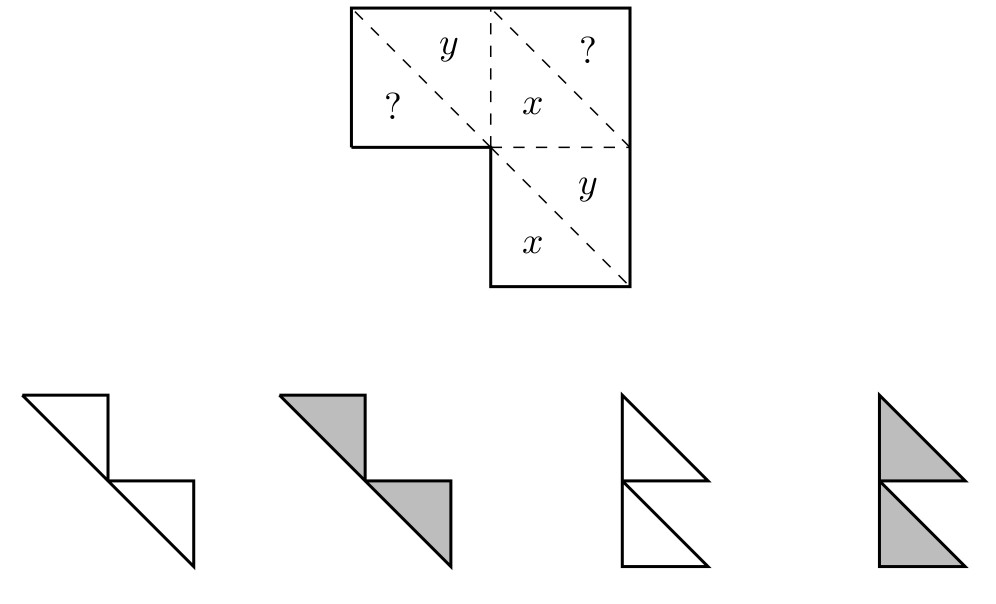
-
21.5.2017 : espace de nombres premiers et pavage du plan par triminos colorés (392)

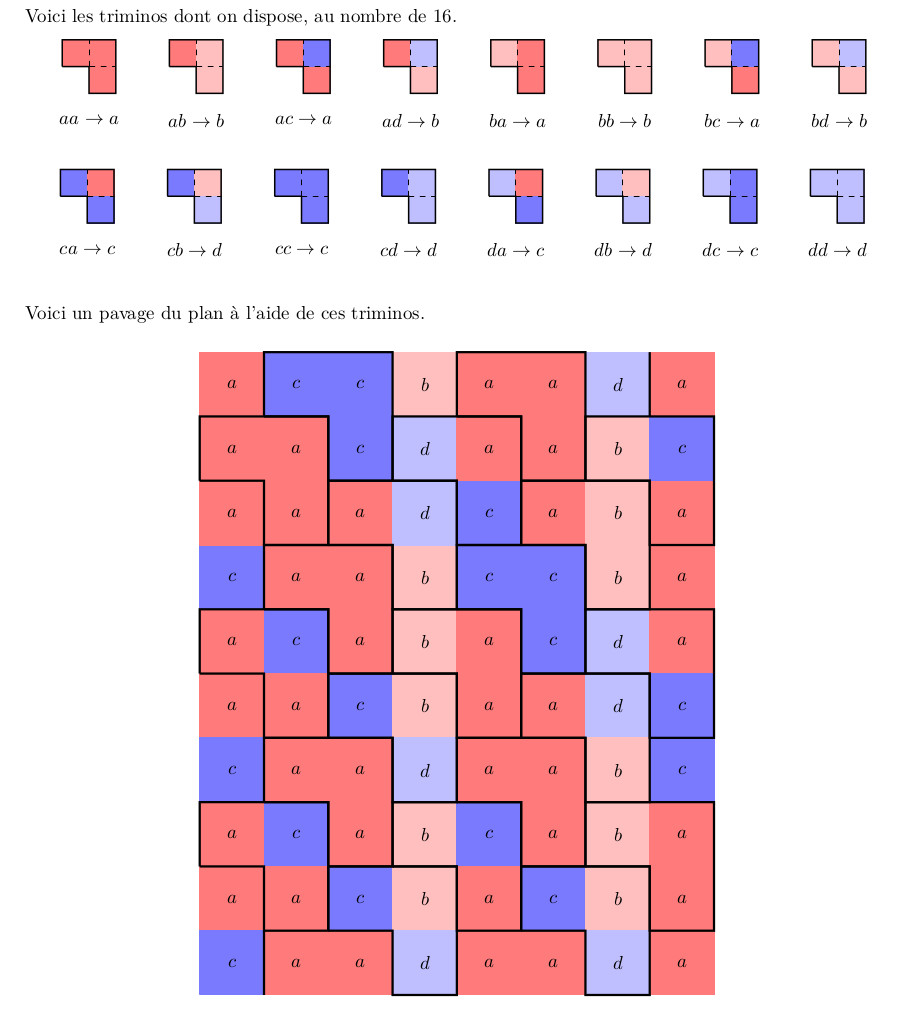
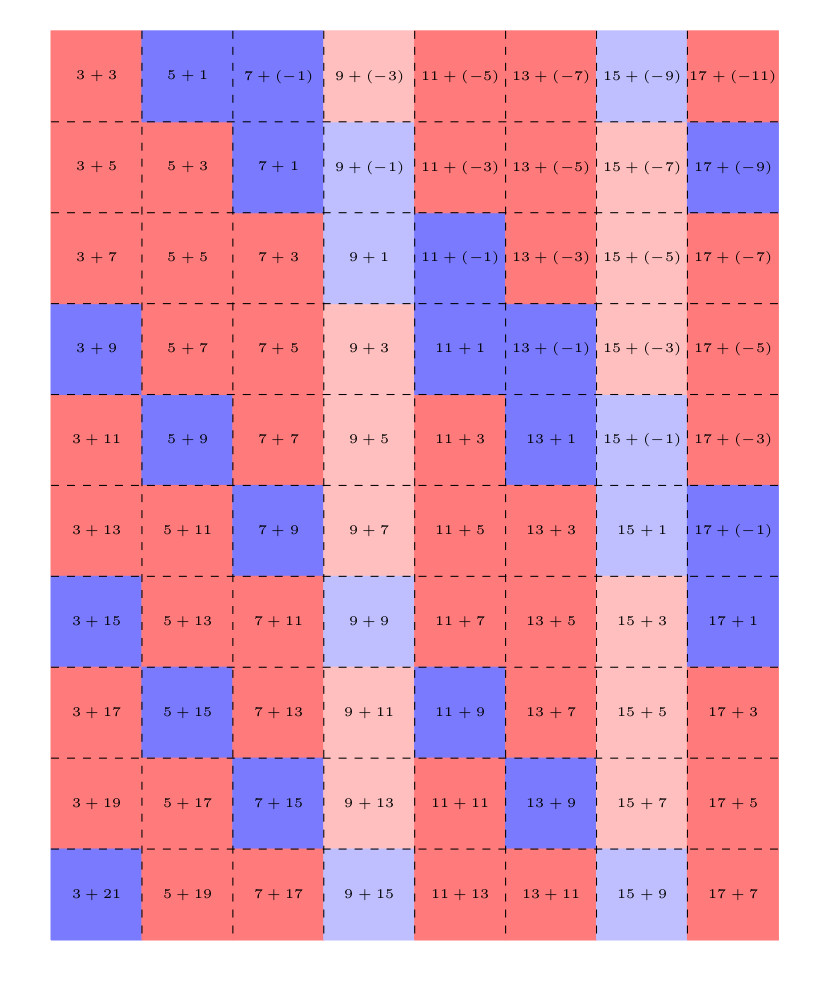
-
20.5.2017 : définition d’un nombre en or : c’est un nombre dans lequel, phonétiquement, on entend un nombre pair et l’un de ses décomposants de Goldbach ; par exemple, 361 est un nombre en or car 61 est décomposant de Goldbach de 300 dans la mesure où 300=61+239 avec 61 et 239 premiers tous les deux. Voici d’autres exemples : 103, 17, 53, 67, 863, 883, 1383. (391)
-
14.5.2017 : Voir les nombres premiers dans le triangle de Pascal (390)

-
8.5.2017 : Chercher à dénombrer exactement (388)

-
30.4.2017 : Polygones modulaires (387)

-
15.4.2017 : Redondire (386)

-
8.4.2017 : images de l’approche par les mots sous hyperboles (385)

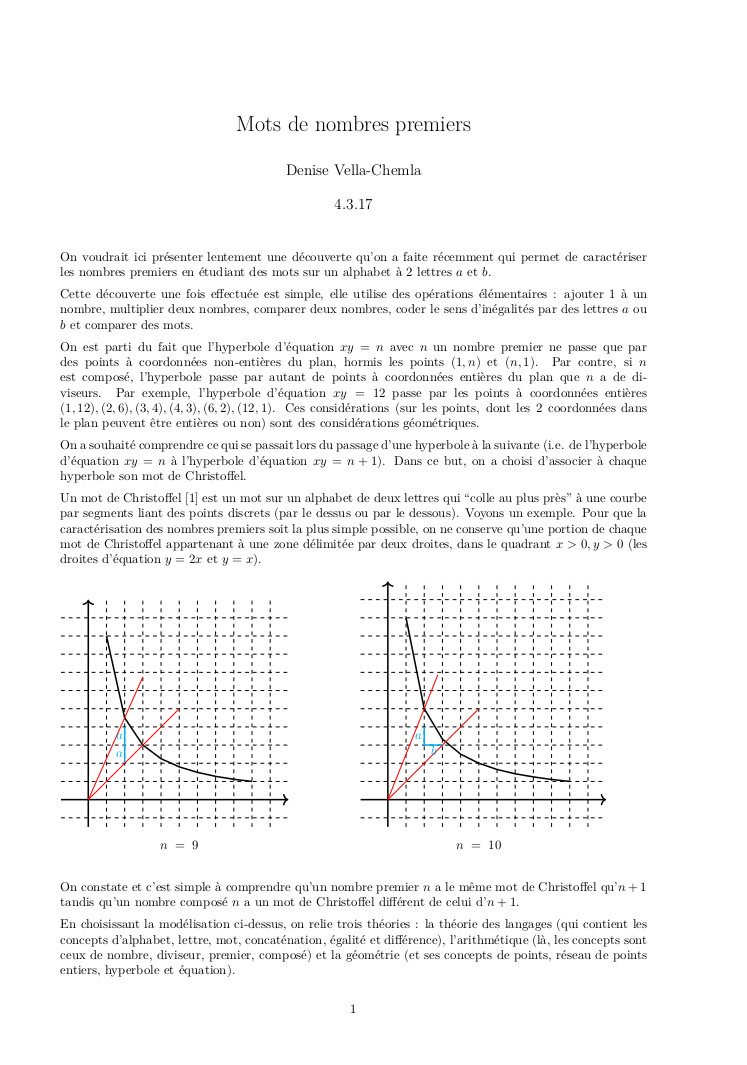
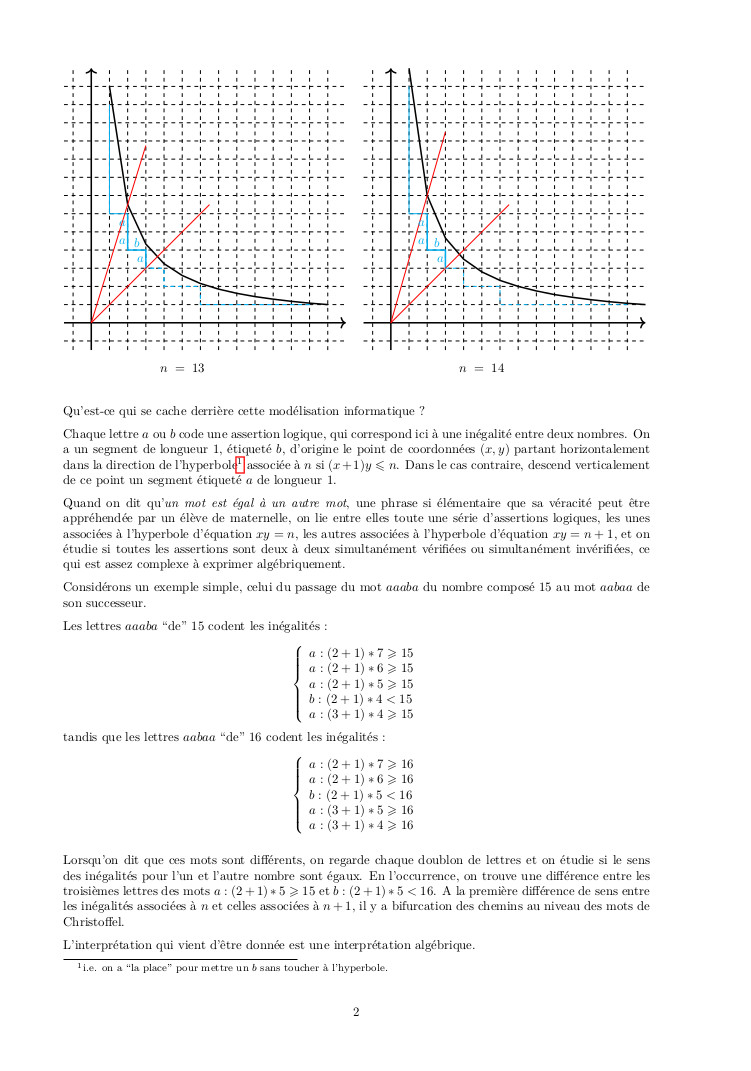


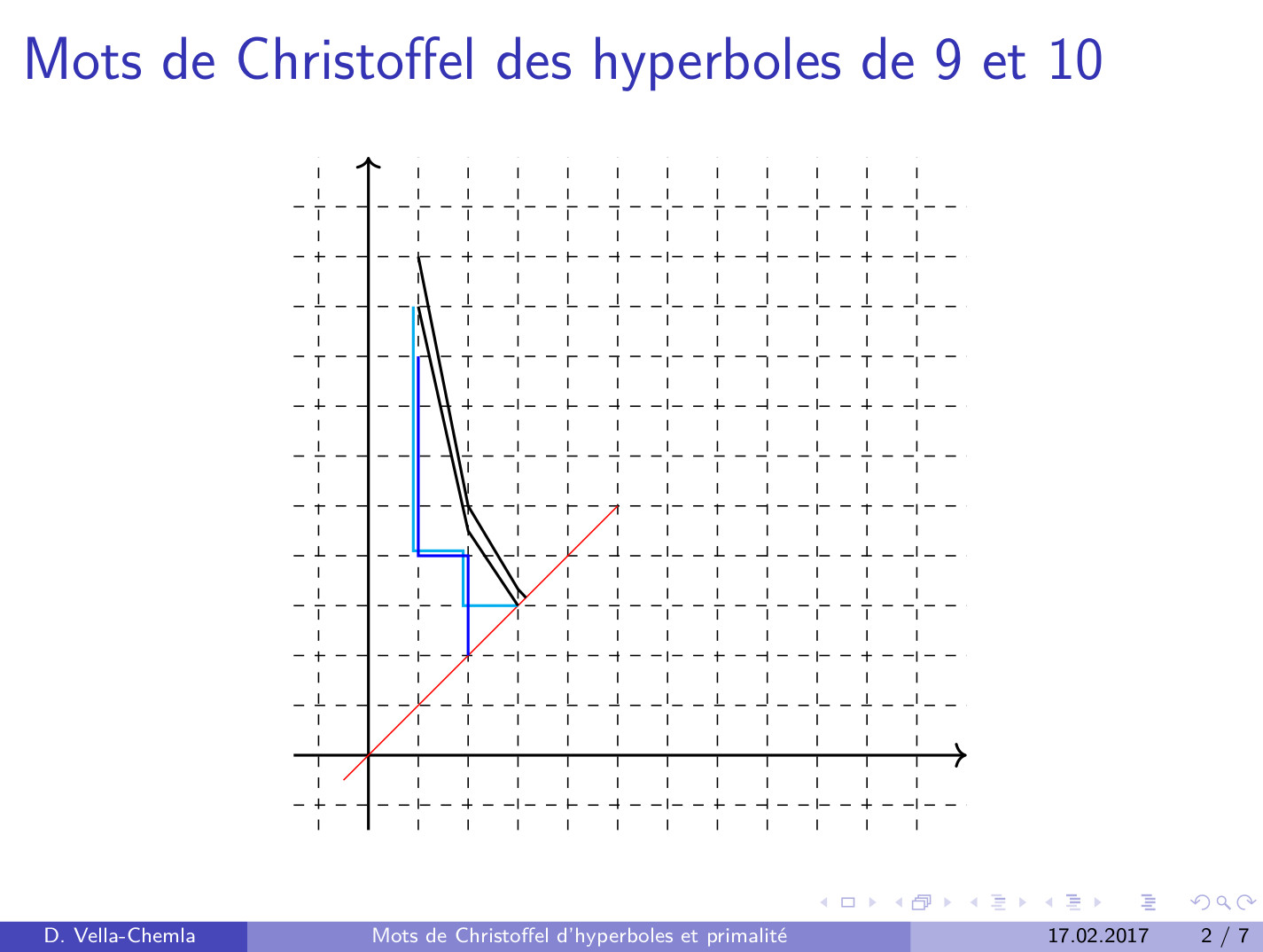
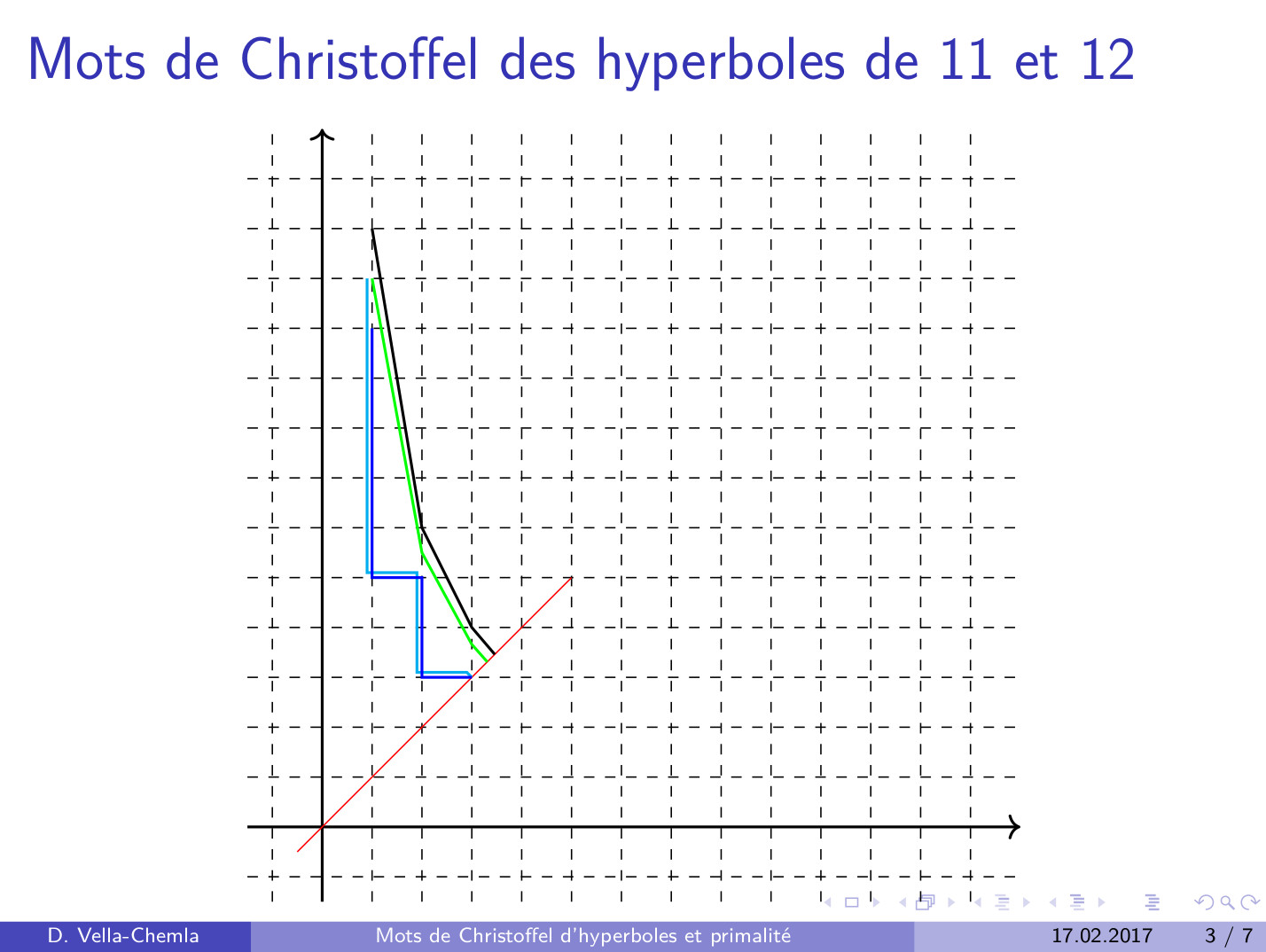




-
2.4.2017 : Nombres premiers, identité des fonctions (384)

-
1.4.2017 : Les plus grands des plus petits (383)

-
31.3.2017 : Comparaison du sens des inégalités deux à deux (382)

-
30.3.2017 : Fonctions sur des inégalités (381)

-
19.3.2017 : Coder les mots booléens par des entiers (380)

-
5.3.2017 : Mots de nombres premiers (379)

-
1.3.2017 : Un programme à mots plus courts pour connaître la primalité des entiers (378)
 Trahtenbrot (programme python) Trahtenbrot (programme python) 
-
28.2.2017 : C’est marrant ! (377)


-
20.2.2017 : Un programme si surprenant pour tester la primalité des entiers : ici, on compte des relations entre 2 assertions logiques (on compare les sens d’inégalités codées par des booléens) et ces relations entre assertions sont aussi des assertions (i.e. sont aussi codées par des booléens). (376)

-
17.2.2017 : Mots de Christoffel d’hyperboles et primalité (375)



-
17.2.2017 : essai de formalisation bicolore (374)

-
16.2.2017 : Comptage de lettres dans des mots de Christoffel (373)

-
15.2.2017 : rassurant ? (372)

-
14.2.2017 : Hyperboles et mots de Christoffel (371)

-
12.2.2017 : compositions puis 22N (370)


  
-
5.2.2017 : Graphe de produits (369)

-
30.1.2017 : Pour qui a du mal à mémoriser l’orthographe des noms de sites, voici un QR-code à flasher pour accèder directement à la page de garde (faire un clic-droit sur l’icône pour enregistrer le QR-code où on veut ; il suffit alors de le flasher avec une application de lecture de QR-code, comme flashcode ou autre, téléchargeable sur ordinateur, tablette ou mobile) (368)

-
29.1.2017 : Points entiers sur hyperboles (367)

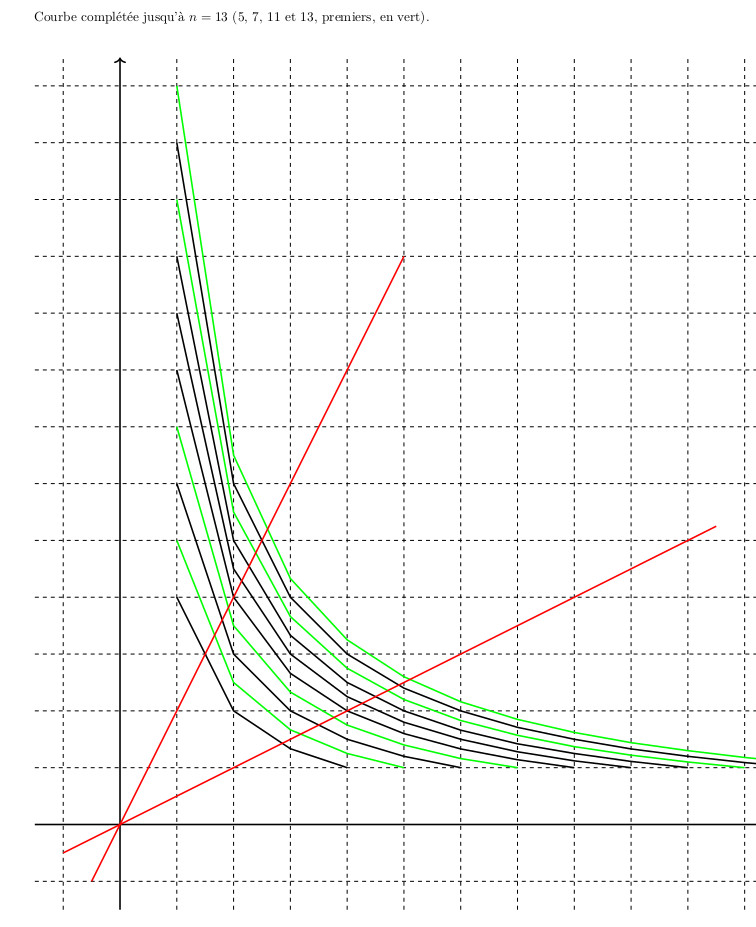
-
23.1.2017 : Hyperboles traversant des mailles (366)

-
17.1.2017 : Compositions & minimiser un périmètre (365)

-
15.1.2017 : Essayer de comprendre comment les points établissent des corrélations entre fonctions
 (364) (364)
Spectres de surfaces vibrantes isopérimétriques
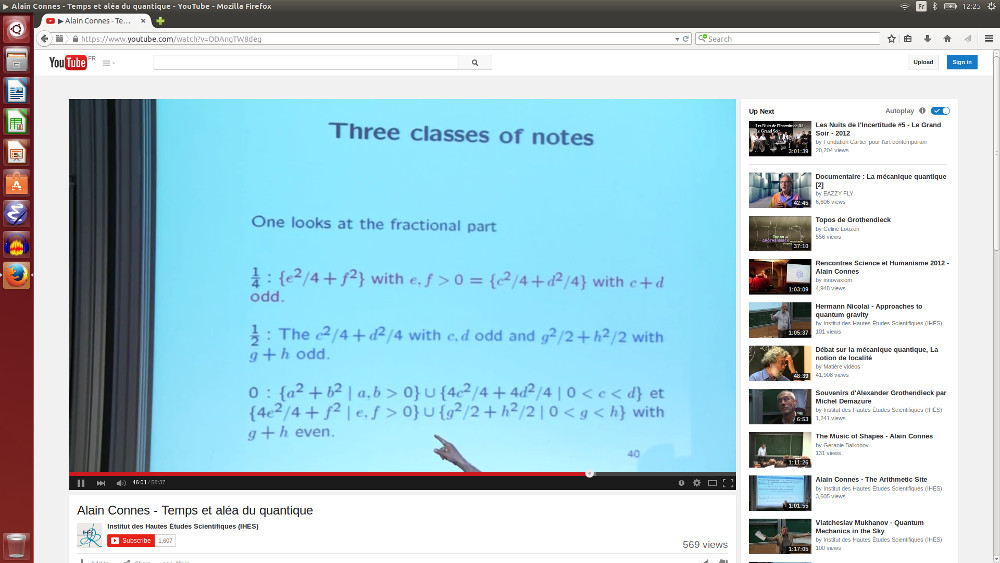  Programme (à la va-vite)
Programme (à la va-vite)
-
5.1.2017 : Suites arythmiques (363)

-
12.11.2016 : la fameuse lettre transcrite en Latex (362)
 
 
-
6.11.2016 : Une récurrence pour l’indicateur d’Euler trouvée dans l’OEIS (361)

-
24.10.2016 : Papier pointé (360)

-
23.10.2016 : Cherche une visualisation parlante (359)

-
Toussaint 2016 : Souvenirs de septembre : problème des officiers d’Euler, Sudokus de l’IHES (358)
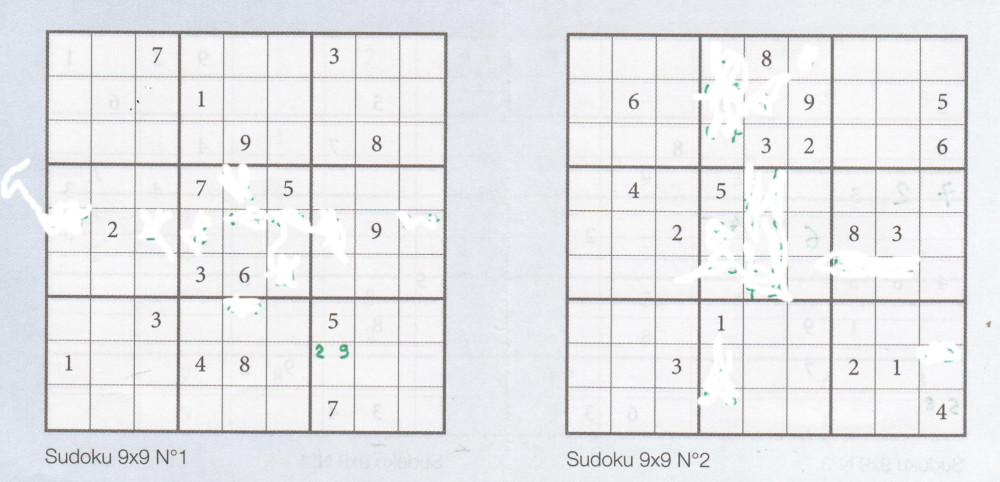
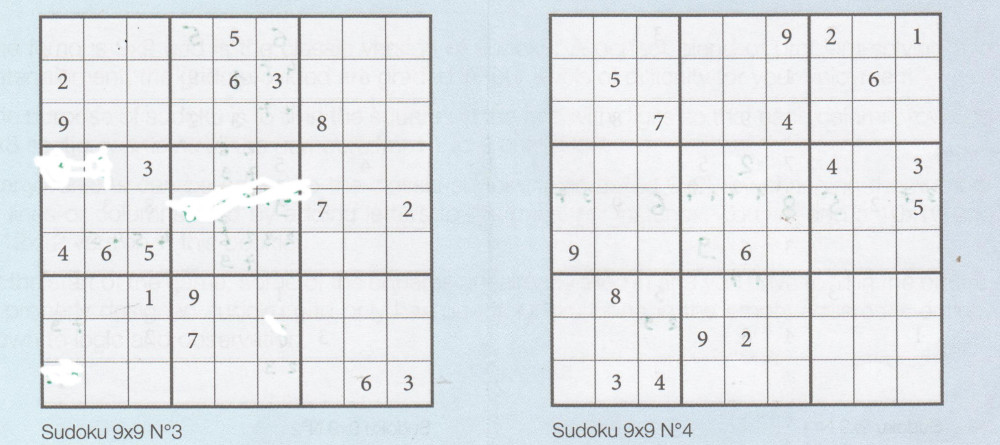













-
23.10.2016 : Pgcd et trajets de booléens (357)

-
22.10.2016 : Pgcd et diagonales de booléens
(356)

-
11.9.2016 : Racines de l’unité (355)
 Programme à la va-vite
Programme à la va-vite Racines de l’unité jusqu’à 500
Racines de l’unité jusqu’à 500 Exposants possibles des racines de l’unité jusqu’à 2016 et indicateurs d’Euler
Exposants possibles des racines de l’unité jusqu’à 2016 et indicateurs d’Euler

-
10.9.2016 : A la recherche d’une formule... constats effectués sur les nombres de résidus cubiques non nuls (ou bien biquadratiques, "quintiques", "sixtiques") puis infirmés mais en faisant une découverte intéressante, à relier peut-être à la propriété de Dedekind évoquée dans les petites questions de fin d’été (on rappelle que les nombres x et p-x ont même résidu de puissance pour les puissances paires et des résidus opposés pour les puissances impaires). (354)

-
7.9.2016 : Distinguer les nombres premiers des nombres composés en suivant l’article 53 des Recherches arithmétiques de Gauss (353)

 Section troisième des Recherches arithmétiques de Gauss
Section troisième des Recherches arithmétiques de Gauss
-
30.8.2016 : Questions de fin d’été (352)

-
28.8.2016 : Nombre de résidus quadratiques des nombres premiers et composés (351)
 en
en
-
27.8.2016 : Dans la thèse de Jenny Boucard "Un "rapprochement curieux de l’algèbre et de la théorie des nombres" : études sur l’utilisation des congruences en France de 1801 à 1850" (9.12.2011), on trouve la référence d’une note de Cauchy aux Comptes-rendus de l’Académie des Sciences du 16.3.1840 dans laquelle Cauchy étudie le nombre de résidus quadratiques d’un nombre inférieurs à sa moitié. Il faudrait comprendre cette note. (350)

-
25.8.2016 : Tables de résidus quadratiques (349)

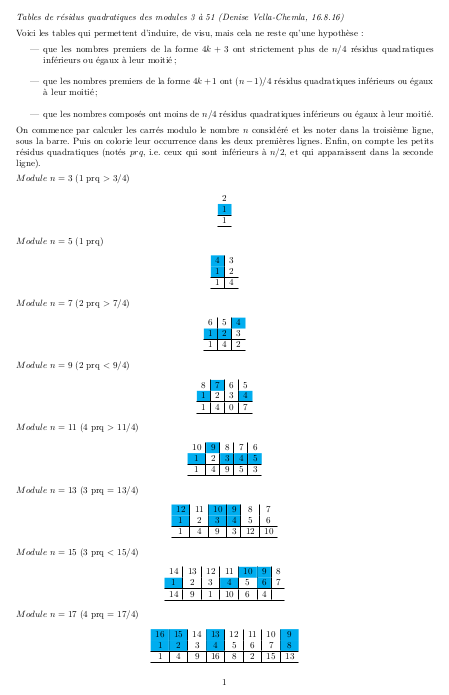 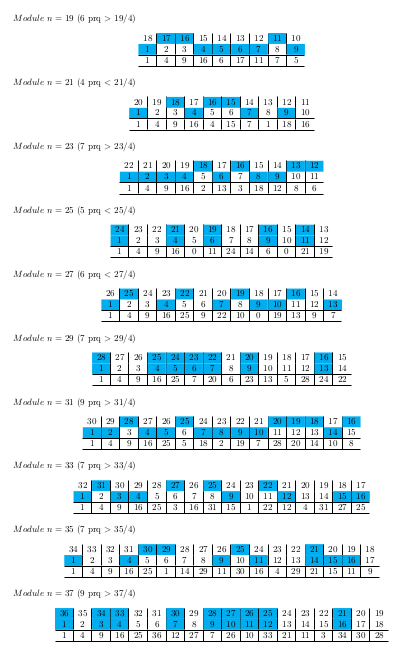 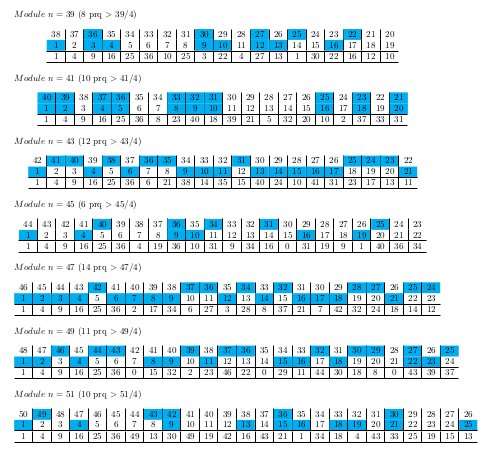
-
25.8.2016 : Table de multiplication modulaire, mod 49, coupée en 2 verticalement. Observer la "presque-symétrie" horizontale sur chaque moitié. A cause de tous les nombres non-premiers à 49=7^2, il y a moins de résidus quadratiques que de non-résidus quadratiques, c’est l’une des causes de l’absence de symétrie. (348)


 
-
25.8.2016 : Nombre de résidus quadratiques d’un nombre entier inférieurs à sa moitié (347)
 (en)
(en)
-
25.8.2016 : Tables de résidus quadratiques
(346)

  
-
19.8.2016 : Peut-être faudrait-il considérer les nombres premiers impairs de la forme 4k+1 comme des produits de la forme (2√k+i)(2√k-i) et les nombres premiers impairs 4k+3 comme des produits de la forme (2√k+1)(2√k-1). (345)
-
19.8.2016 : Soient deux opérateurs du plan: (344)
f qui échange les coordonnées et g qui oppose la première coordonnée.
Faisons les agir l’un avant l’autre, puis l’un après l’autre sur un point (x,y).
Dans le premier cas (g ○ f), on obtient :
(x,y) → (y,x) → (-y,x).
Dans le second cas (f ○ g), on obtient :
(x,y) → (-x,y) → (y,-x).
Rotation horaire, rotation anti-horaire, "remonter" le temps.
-
19.8.2016 : Ce qui est plaisant, ce n’est pas tant de voir la pensée en mouvement, c’est plutôt d’éprouver ce qui la fait accélérer. (343)
-
17.8.2016 : De visu (342)

-
16.8.2016 : Plus de la moitié (341)

-
12.8.2016 : Nombre de résidus quadratiques d’un nombre entier inférieurs à sa moitié (340)

-
2016 : Images (339)


-
4.8.2016 : Revenir à la somme des diviseurs d’Euler (338)

-
2.8.2016 : en tentant de fabriquer des couples de nombres premiers d’écart 2 comme s’il en pleuvait, on a trouvé 7 couples sympathiques, parce qu’on les obtient par multiplication : (337)
72 = 6.12 = 4.18, ou bien 108 = 6.18, ou encore 432 = 6.72 = 4.108 ou enfin 2592 = 6.432. Les factorisations de ces nombres contiennent exclusivement des 2 et des 3.
Les couples sympathiques sont (5,7), (11,13), (71,73), (17,19), (107,109) (431,433) et (2591,2593). Ce sont leur "pairs" qu’on multiplie.
Se reporter à ces pages pour tester la primalité


-
1.8.2016 : Etudier des nombres d’écarts (336)

-
17.7.2016 : Continuer (335)
 



-
10.7.2016 : Tout nombre est somme de 3 nombres triangulaires ou somme de 4 nombres carrés. (334)
Décomposition des nombres en 3 triangulaires en C++
Décomposition des nombres en 4 carrés en C++
Décomposition des nombres en 3 triangulaires en python
Décomposition des nombres en 4 carrés en python
Eureka de Gauss
 Lien vers le journal de Gauss
Lien vers le journal de Gauss
Résultat du programme de décomposition en trois triangulaires
Résultat du programme de décomposition en quatre carrés
-
3.7.2016 : Conjecture de Goldbach : programme en Python au lieu de C++ (333)

-
25.6.2016 : Images (332)

-
19.6.2016 : Polygones, circuits (331)

-
26.6.2016, 12.7.2016: essais oubliés (330)
 Si j’avais essayé de programmer, j’aurais vu qu’on peut difficilement obtenir un carré avec tous ces croisements... Si j’avais essayé de programmer, j’aurais vu qu’on peut difficilement obtenir un carré avec tous ces croisements...



-
12.6.2016 : Tamis, inéquations quadratiques
(329)

-
7.6.2016 : 2016 - 1742 = 274

-
22.5.2016 : Images parlantes


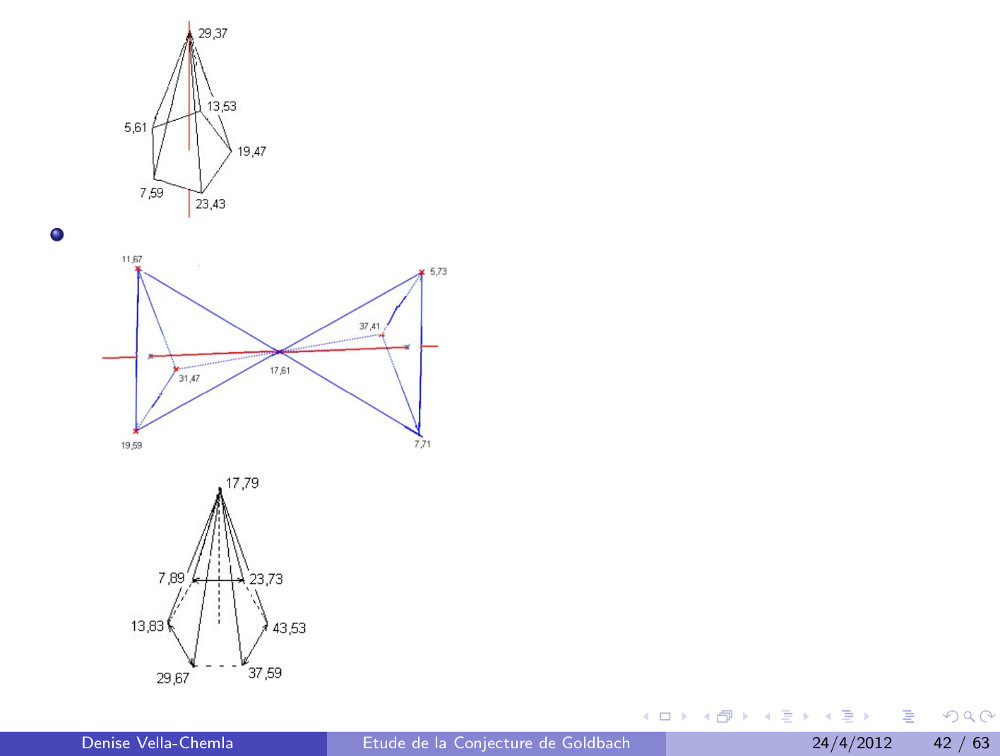
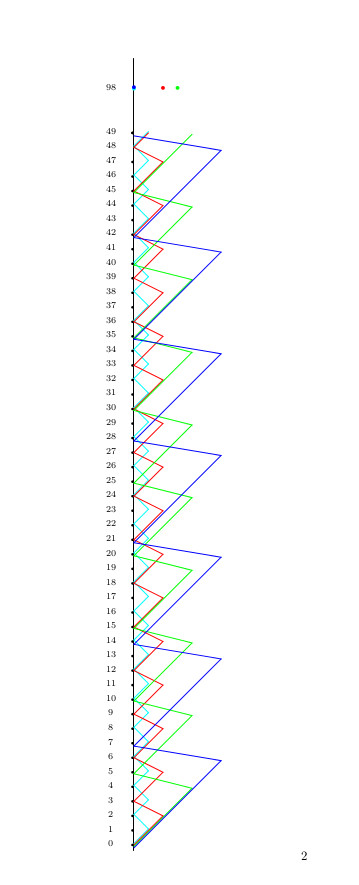




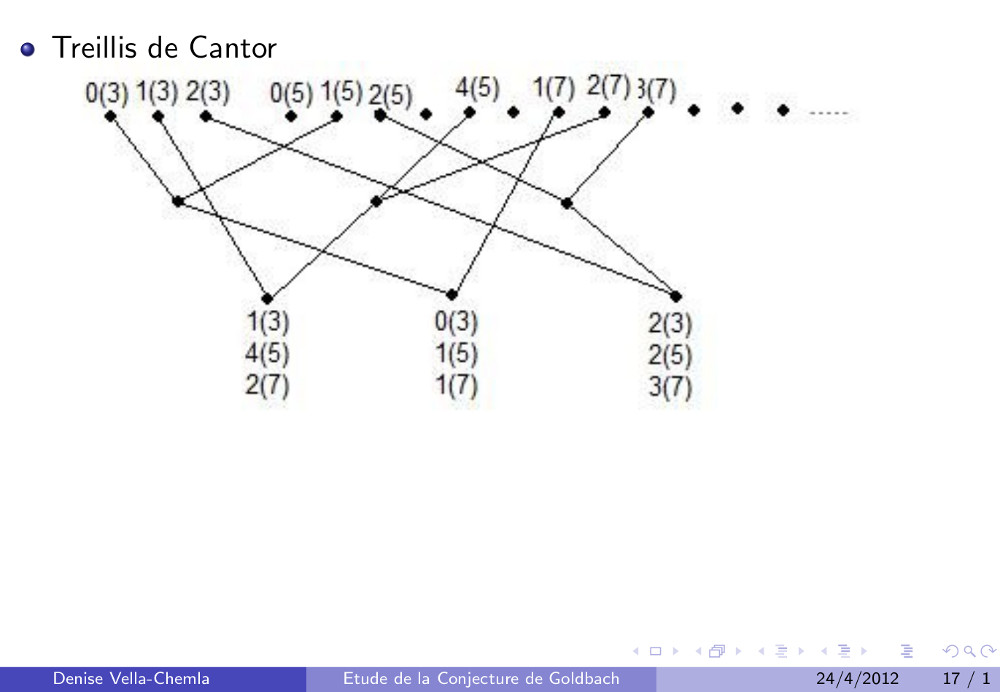
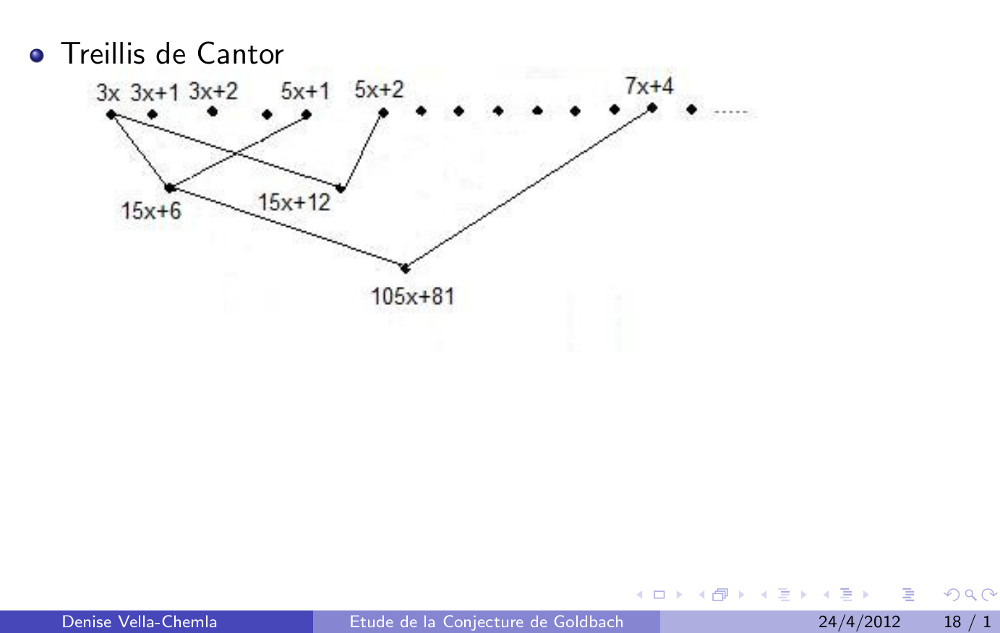

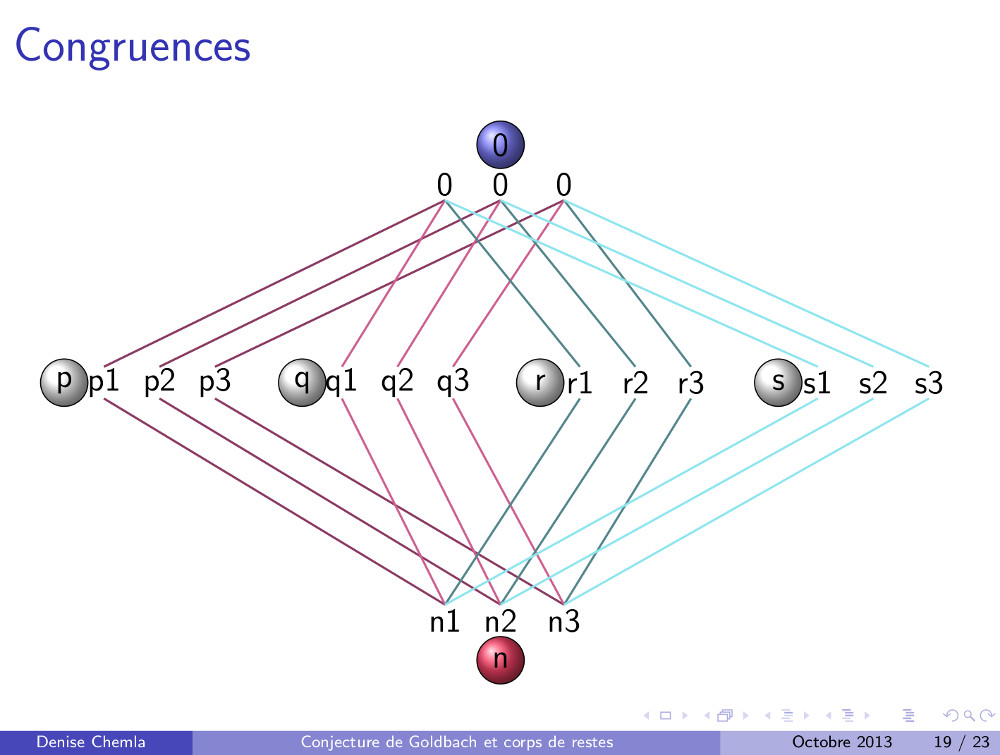

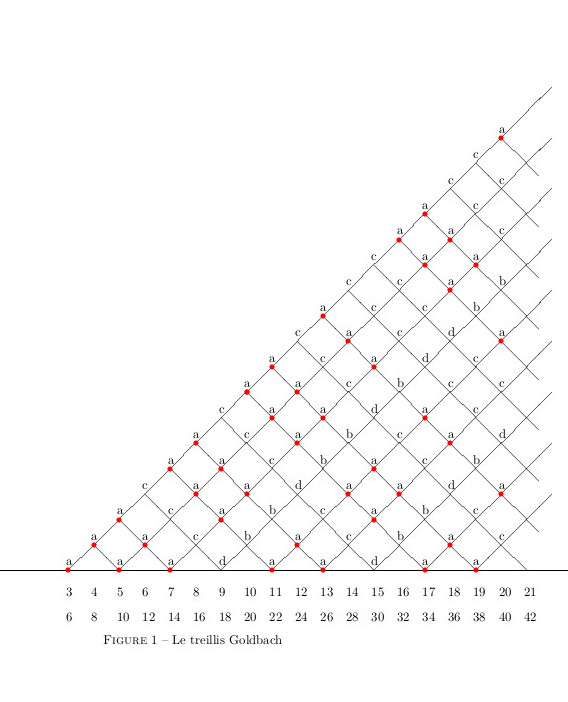

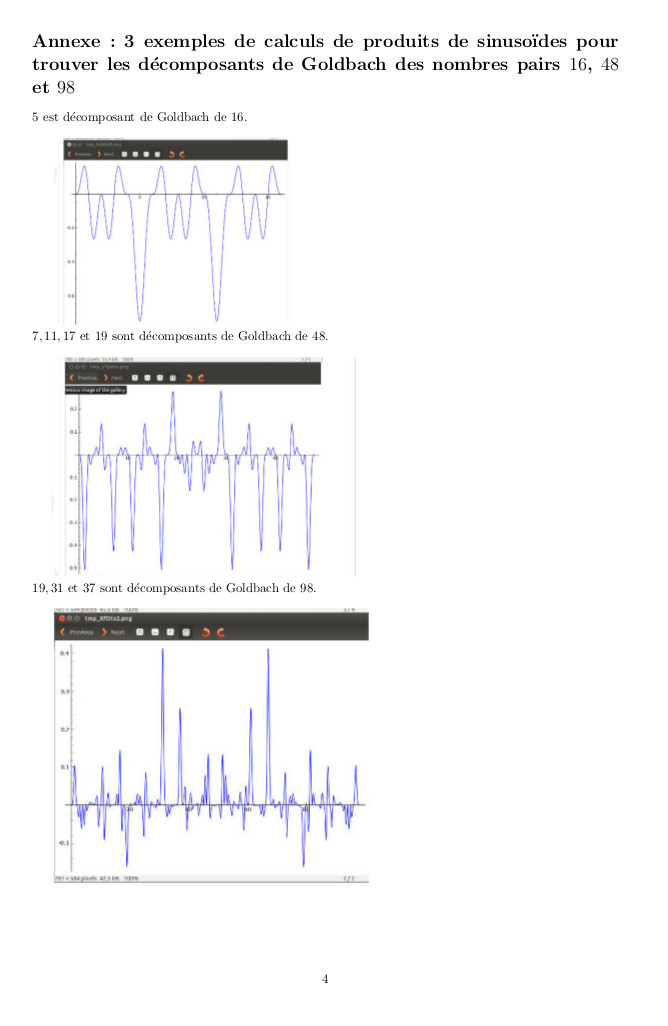
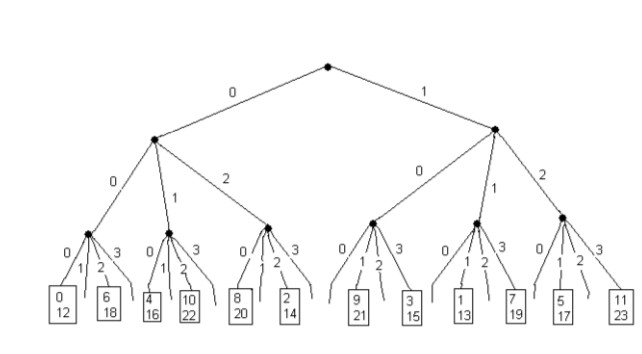

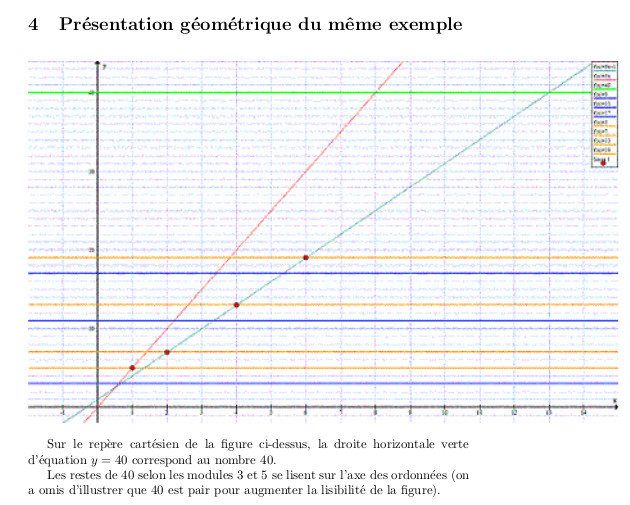
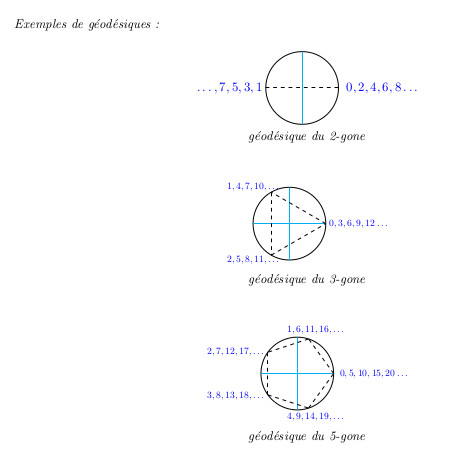
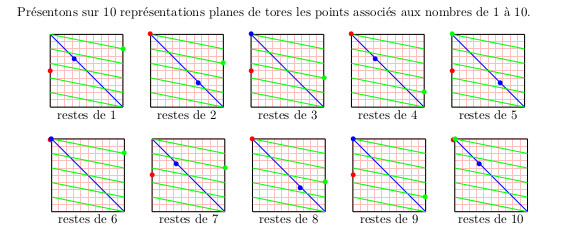












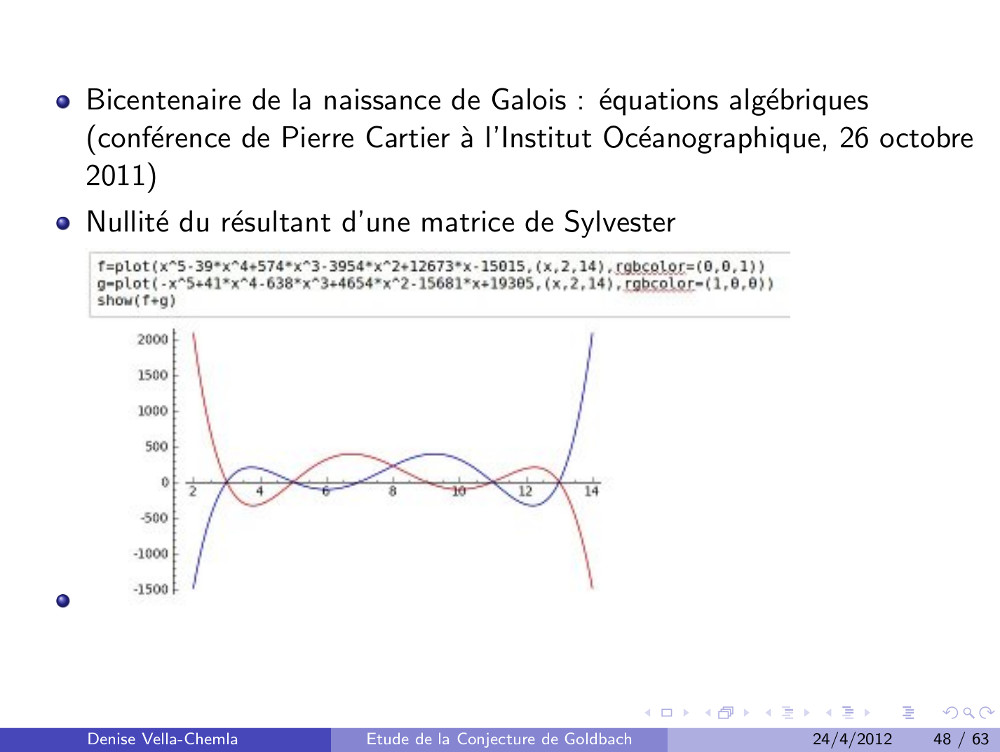




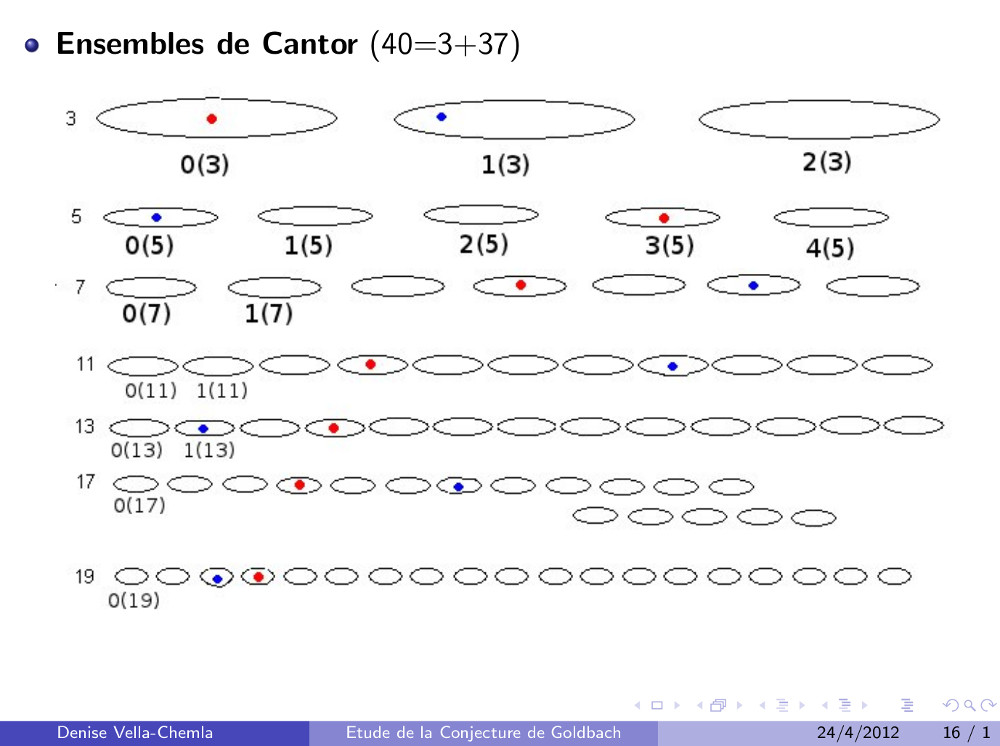
-
21.5.2016 : Coder pour jouer (328)

-
21.5.2016 : Programme préféré : somme de cosinus (327)

-
17.5.2016 : Insularité des nombres premiers (326)


-
14.5.2016 : Initiale G (325)

-
14.5.2016 : Premiers en 3D, symétrie centrale (324)

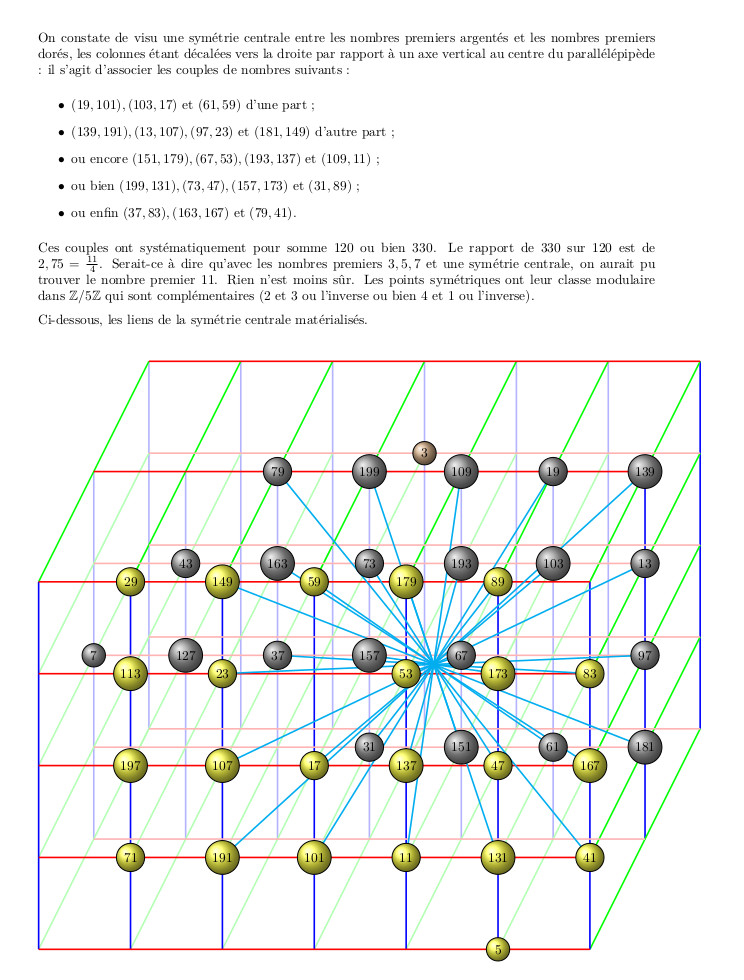 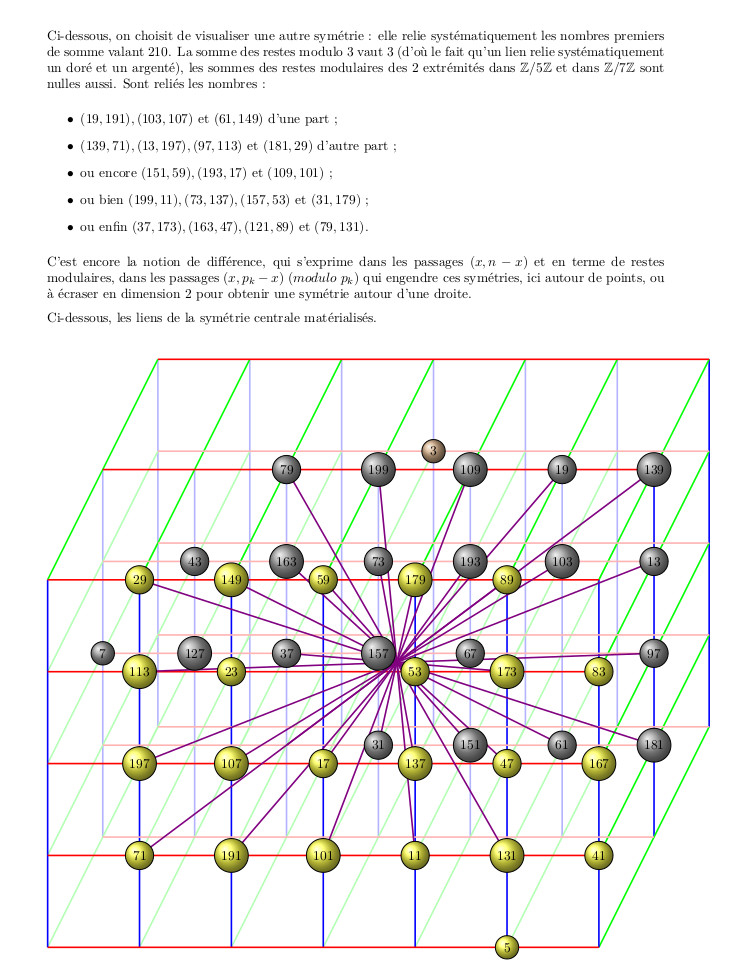
-
13.5.2016 : Premiers en 3D, pelote embrouillée (323)

-
10.5.2016 : Snurpf, reprisé (322)

-
8.5.2016 : Infiniment tore (321)


-
5.5.2016 : Cromagnon child (320)

-
4.5.2016 : Entrelacs premiers (319)

-
29.4.2016 : Pgcd tropical (318)

-
26.4.2016 : Rectangles (317)

-
26.4.2016 : cette nuit, la fusée Soyouz a décollé de Kourou pour lâcher dans l’espace le satellite Microscope (ainsi qu’un autre satellite). Ce petit laboratoire de l’espace est destiné à vérifier l’expérience de Galilée (tous les corps en chute libre tombent à la même vitesse) avec une précision inégalée (10-15). Souvenirs d’une belle expérience scolaire en lien avec la société ArianeEspace (tous les élèves avaient été très fiers de recevoir un pin et un stylo-fusée Ariane, pour les récompenser de leur investissement et de la pertinence de leurs questions.) (316)

-
24.4.2016 : Entiers de prince (315)

-
21.4.2016 : Nouvelle sidérante (ade4il2norstuv), Denise Vella tourne (ade4il2norstuv)... en rond ! Mieux ça que foncer dans le mur. (314)

-
8.4.2016 : Matrices gigognes (313)

-
6.4.2016 : Transitions (312)

-
6.4.2016 : Entrechocs, entrelacs (311)

-
29.3.2016 : Champ de lettres (310)

-
26.3.2016 : Matrices idempotentes (309)

-
20.3.2016 : Petit pont vers la mécanique quantique (308)

-
6.3.2016 : Je crois avoir atteint mon objectif en étudiant essentiellement 4 booléens.
On pourrait peut-être établir un pont vers une matrice de densité 2x2 composée de 4 éléments de valeur 1/2 ; cette matrice est la matrice d’une projection sur la diagonale principale, elle est idempotente. (307) 
-
13.2.2016 : Ecriture p-adique, écriture en base p (306)

-
8.2.2016 : Premiers les plus proches possible (305)

-
5.1.2016 : Pierre Boulez : Constellation-Constellation reflet, points, blocs, forme ouverte ou bien Répons.
"Un coup de dés jamais n’abolira le hasard" (Stéphane Mallarmé)
 Une vidéo de la collection "la mémoire du Collège de France"
Une vidéo de la collection "la mémoire du Collège de France"


-
3.1.2016 : Doubles de pairs entre deux nombres premiers, comptages de lettres, régularités (304)

-
2.1.2016 : Comptages de lettres, régularités (303)

-
12.12.2015 : Nombres premiers d’écart 2 et mots (302)

-
3.12.2015 : Pépite pour groupies (extrait d’une lettre de Donald Knuth à Antony Hoare, dans un transparent de Thierry Coquand, le concepteur de Coq - issu de sa présentation Théorie des types dépendants et axiome d’univalence - projet CATHRE) (301)

-
2.12.2015 : Nombres premiers d’écart 2 qui voient leurs restes perturbés (300)

-
1.11.2015 : Projections (299)

-
31.10.2015 : Champ de lettres (298)

-
19.10.2015 : C’est la première fois que je lis une portion du paragraphe contenant la fameuse citation de David Hilbert, extraite de son discours au Congrés des mathématiciens de 1900 à Paris ; l’extrait est encore plus sublime que la phrase seule : "Il ne faut pas croire ceux qui, aujourd’hui, avec un air philosophique et d’un ton supérieur, prédisent la décadence culturelle et se complaisent dans l’ignorabimus. Pour nous, il n’y a pas d’ignorabimus et selon moi, surtout pas en sciences. Au lieu d’un ignorabimus insensé, notre devise doit être au contraire : "nous devons savoir, nous saurons". (297)
-
30.9.2015 : Cherche une maille de taille 4 pour le tissage (296)

-
12.9.2015 : Revenir au maillage (295)

-
12.9.2015 : Opérateurs sans intérêt (294)

-
8.9.2015 : Tête qui tourne (une carte antipodale permet de situer le point opposé d’un point sur la sphère) (293)

-
24.8.2015 : Un cadeau ! (292)

-
24.8.2015 : Distance suprême (291)

-
♥ 1.8.2015 : Calculer l’indicateur d’Euler des nombres par un calcul matriciel (290)
 janv. 2026 janv. 2026 
-
30.7.2015 : Spectres (289)

-
♥ 29.7.2015 : Calculer les sommes de diviseurs par un calcul matriciel (288)
 janv. 2026 janv. 2026 
-
♥ 27.7.2015 : Matrices, sommes de diviseurs, produits de restes (287)

-
26.7.2015 : Continuer à chercher... un calcul matriciel (286)

-
18.7.2015 : Sommes de cosinus et polynômes de Tchebychev (285)

-
16.7.2015 : Sommes de cosinus et matrices (284)

-
15.7.2015 : À tore ou à raison ? (283)

-
14.7.2015 : Une citation d’Einstein, extraite de sa biographie par Abraham Pais "Subtle is the Lord" : "ce qui a peut-être été négligé, c’est l’irrationnel et l’incohérent, la drôlerie, voire la déraison que la nature, dans son activité inépuisable et, semble-t-il, pour son propre amusement, implante en chaque individu. Mais ces éléments, seul l’individu peut les discerner dans le creuset de son esprit". (282)
-
12.7.2015 : Tore et divisibilité (281)

-
10.7.2015 : "surface d’n pair" trouvée sur le forum les-mathematiques.net (euh, non, "surface d’Enneper") (merci au dessinateur) (280)

-
7.7.2015 : Epingler les restes modulaires sur le tore (279)

 9.7.2015 :
9.7.2015 : 
-
24.6.2015 : Matrices d’entiers et découverte merveilleuse d’Euler concernant la somme des diviseurs (278)

-
23.6.2015 : Discret / continu (277)

-
20.6.2015 : Autres petites idées (276)

-
17.6.2015 : Petites idées (275)

-
23.5.2015 : Moments chantés, môme enchantée (274)

-
11.5.2015 : Rêves sonores, rêves aquatiques (273)

-
11.5.2015 : Arpenter la sphère (272)

-
22.10.2014 : Relations invariantes entre nombres de décompositions de Goldbach codées dans un langage à 4 lettres (271)

Les variables doivent représenter des nombres d’assertions logiques sur les nombres plutôt que les nombres eux-mêmes
-
23.10.2014 : Invariant relations between binary Goldbach’s decompositions’numbers coded in a 4 letters language (270)

-
23.10.2014 : Poincaré à propos du raisonnement par récurrence, Euler à propos de la démonstration et Hardy à propos des créations des mathématiciens (269)

-
9.11.2014 : George Boole est un mathématicien britannique, créateur de la logique moderne, l’algèbre de Boole. Il est autodidacte et a exercé un temps le métier d’instituteur. Son but était de traduire des idées et des concepts en équations. Son algèbre binaire utilisent deux valeurs dites "de vérité" : 0 et 1. L’informatique repose sur la notion de bit, l’unité d’information binaire. On appelle variable booléenne une variable qui peut prendre l’une de ces deux valeurs exclusivement : 0 ou 1. (268)
-
d’octobre 2005 à octobre 2014 :
Merci à Donald Knuth, merci aux inventeurs de Wikipedia et Google, et merci à tous les professeurs et à toutes les institutions qui mettent en ligne gratuitement des articles scientifiques dont on peut essayer d’étudier les idées.
Merci également à la communauté du Libre (OpenSource community) pour avoir mis gratuitement à notre disposition le système d’exploitation Ubuntu, les logiciels ou langages ou bibliothèques gnu-emacs, pdflatex, asymptote, tikz, Filezilla et à une certaine société française qui héberge le site.
Merci à Daniel Diaz, concepteur de GNU-Prolog et de CLP(FD) (un langage de programmation dont l’acronyme signifie Constraint Logic Programming in Finite Domains), pour les sympathiques échanges et la bibliothèque GB-Tools d’outils dédiés à CG (hiver 2010-2011). Et merci à Dominique Ceugniet pour ses programmes optimisés.
Merci aux vulgarisateurs scientifiques, pour le bien-être que procurent leurs articles, émissions radiophoniques, films.
Et enfin, mes remerciements chaleureux à Annick Valibouze, Claude-Paul Bruter, Yves Meyer et Alain Connes, qui m’ont reçue et aidée. (267)
-
13.12.2014 : Qui, quand, où ? (266)

-
18.3.2015 : Extrait d’un essai de Werner Heisenberg La partie et le tout

-
Petite expérience vécue : Calculer avec des élèves de CM2 (ou CM1, ou CE2) la vitesse approximative de rotation de la Terre sur son orbite autour du soleil en km / h et voir alors ses élèves se retourner tous ensemble pour regarder par la fenêtre ! (265)
-
Textes (264)

-
Liens vers la physique quantique et textes (263)



Einstein, Podolsky, Rosen (EPR)
 Bell
Bell

Extraits de La nature de la physique de Richard Feynman

Un site superbe : plusieurs petites animations très chouettes qui expliquent certains effets quantiques

Collège de physique et de philosophie (3.10.2011)

-
Qui est qui ? (262)

-
21.10.2014 : Pour ceux qui aiment bien s’abaisser les dioptries et les dixièmes, un programme et son résultat (261)

 en python
en python 
-
20.10.2014 : Résumé de l’observation des relations invariantes entre nombres de décompositions de Goldbach codées dans un langage à 4 lettres (260)

-
14.9.2014 : dans la note du 17 mai, j’ai commis une grossière erreur page 8 ;
je vais essayer de la corriger en utilisant uniquement des démonstrations par récurrence (pages 6, 7 et 8) ; remerciements à D.Perrin qui a lu ma note et signalé l’erreur. (259)
-
5.8.2014 : Nuage rose le soir, de beau temps, l’espoir...
-
10.7.2014 : Primalité et zéros de sommes de cosinus ♥(ou bien "elle c’est simple, je l’adore !", première rencontre) (258)

-
19.6.2014 : Calcul simplifié de la somme des diviseurs (257)

-
23.5.2014 : Gauss a écrit : "Le problème de distinguer les nombres premiers des nombres composés et de décomposer ceux-ci en leurs facteurs premiers est connu comme un des plus importants et des plus utiles de toute l’Arithmétique. [...] En outre, la dignité de la Science semble demander que l’on recherche avec soin tous les secours nécessaires pour parvenir à la solution d’un problème si élégant et si célèbre."
-
17.5.2014 : Conjecture de Goldbach, langage à 4 lettres, variables et invariants (256)







-
♥ 17.5.2014 : continuer de suivre Galois (ajout du problème des nombres premiers d’écart 2) (255)



-
11.5.2014 : Un beau souvenir de 2005 : empilement de valuations p-adiques, en continuant de suivre Laisant (254)

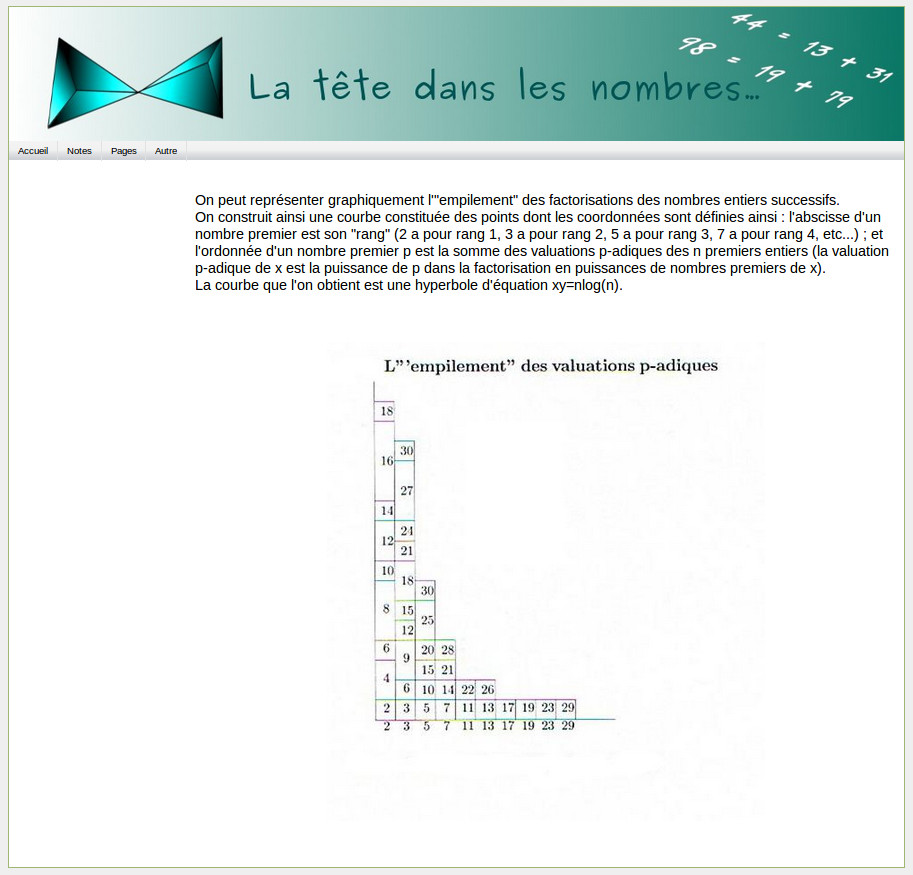
-
26.4.2014 : Essayer de remonter à la source des idées (253)

-
26.4.2014 : La leçon de mathématiques absurdes d’Eugène Ionesco (252)

-
23.4.2014 : Conjecture de Goldbach, langage à 4 lettres, variables et invariants (251)



-
18.4.2014 : Conjecture de Goldbach et langage à 4 lettres, grâce à l’aide de Claude que je remercie (250)

-
16.4.2014 : Les nombres sont des mots (249)

-
12.4.2014 : Diaporama Les nombres sont des mots (248)


-
12.4.2014 : Observer les mots (247)


-
12.4.2014 : Positionner les décompositions triviales de Goldbach sur la droite du plan complexe de partie réelle 1/2 (246)

-
28.3.2014 : Les points du maillage commutent-ils ? (245)

-
...27.3.2014 : On peut oublier l’indéterminisme sur la première lettre des mots en utilisant des mots infinis des deux côtés... (244)
-
27.3.2014 : Mots bouclés (243)

-
26.3.2014 : Programmer la note Découverte d’une loi tout extraordinaire des nombres par rapport à la somme de leurs diviseurs (242)

 6.4.2025 : programme python 6.4.2025 : programme python 
-
Euler et sa loi tout extraordinaire des nombres par rapport à la somme de leurs diviseurs (241)
 calculer les sommes de diviseurs par un calcul matriciel
calculer les sommes de diviseurs par un calcul matriciel

 
-
23.3.2014 : Conjecture de Goldbach et mouvement brownien, mais l’indéterminisme sur la première lettre des mots reste patent (on jette l’éponge) (240)
 (in english (in english  ) )
-
22.3.2014 : Retrouver Euler et son indicatrice (239)

-
calculer les indicateurs d’Euler par un calcul matriciel (238)

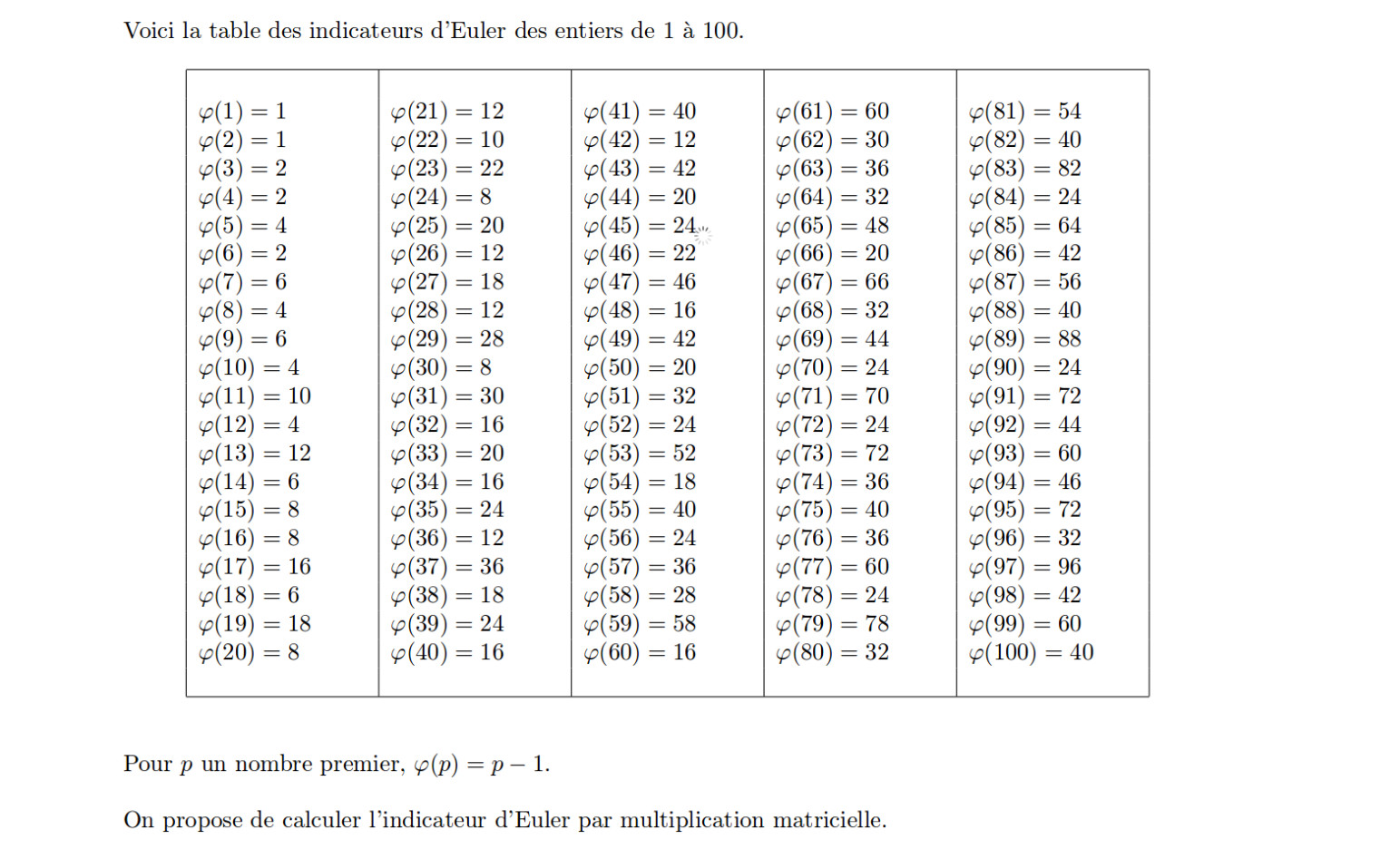
-
22.3.2014 : Récurrence mystérieuse pour la somme des diviseurs (237)

-
22.3.2014 : Des règles de réécriture et un indéterminisme patent complètement décourageants (236)

-
20.3.2014 : 1 monoïde, 2 booléens, 4 lettres, 16 règles, 1 invariant et des changements de parité (a+c fonction en espalier qui compte les doubles de premiers) (235)

-
21.2.2014 : Le petit baluchon (234)

-
16.2.2014 : Conjecture de Goldbach : écrire, réécrire, compter (233)

-
12.2.2014 : Conjecture de Goldbach, langage, réécriture (232)

-
8.2.2014 : où l’on retrouve le maillage d’octobre 2005 (231)

 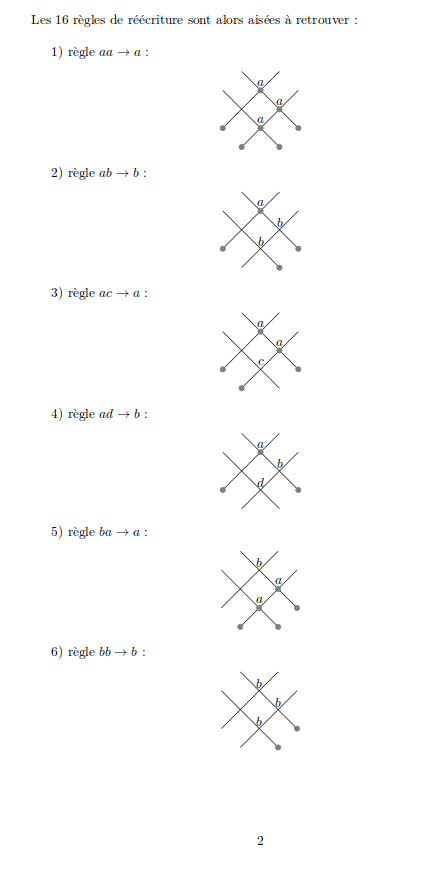 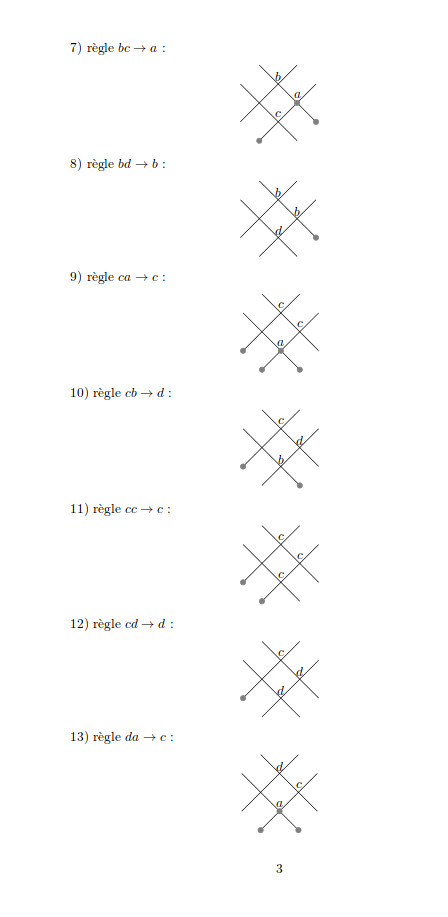  
-
5.2.2014 : Le petit livre orange de Trahtenbrot du professeur Yves Césari (que je remercie, ainsi que Michel Chein, Olivier Cogis, Jean-Paul Bordat, Hervé Dicky, Eric Terouanne, Max Vincent, Pierre Dujols, et les autres) qui traite entre autres du problème du mot (230)















 
-
4.2.2014 : conjecture de Goldbach, mots booléens, parité, imparité, invariant (229)

-
30.1.2014 : Conjecture de Goldbach, mots booléens, invariant (228)

-
18.1.2014 : Leçons de solfège et de piano (227)

-
18.1.2014 : Conjecture de Goldbach, mots booléens et LRQ (226)

-
13.1.2014 : Une drôle de relation (225)

-
12.1.2014 : Tirettes de Charles-Ange Laisant (224)


-
11.1.2014 : Mots cycliques (mots gris, mots bleus) conservant une lettre 0 par permutations (223)

-
4.1.2014 : Anagrammes de mots de restes (222)

-
30.12.2013 : Pierre Boulez : rechercher des formes
 (221)
Grilles (221)
Grilles
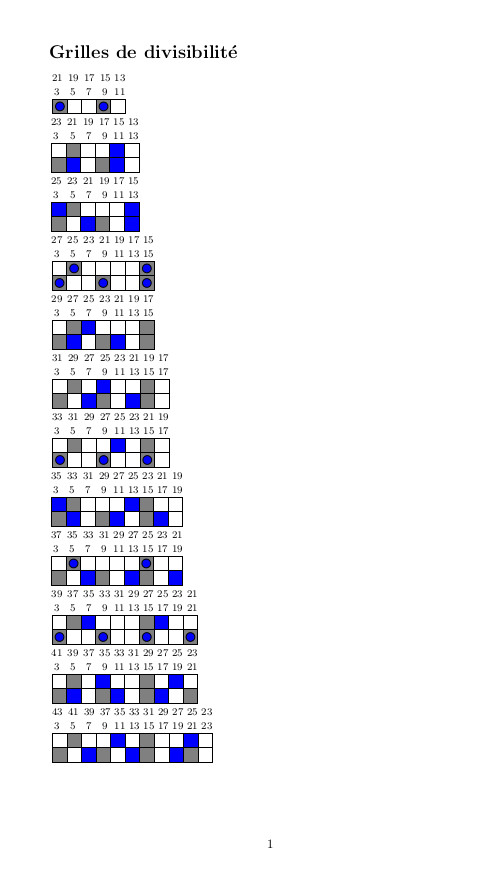
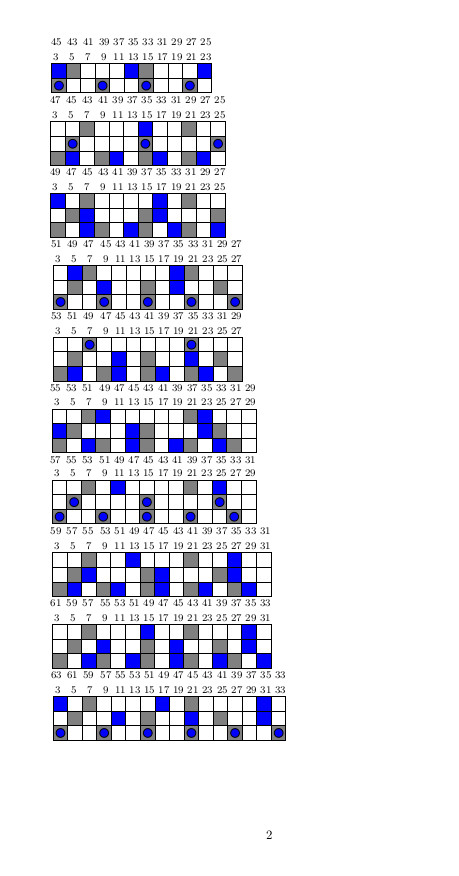


-
♥ 23.12.2013 : Analogie (220)

-
21.12.2013 : Continuer de suivre Galois (219)


-
18.12.2013 : Yves Meyer (que je remercie) présentera la preuve d’Harald Helfgott le 30 janvier, lors d’une conférence intitulée "Preuve de la conjecture de Goldbach", aux lycéens du Lycée Lakanal de Sceaux
 Yves Meyer a reçu le Prix Abel en 2017. Yves Meyer a reçu le Prix Abel en 2017.  (218) (218)
-
Sinusoïdes (217)

-
18.12.2013 : Résumé de l’approche par le produit des sinusoïdes (traitement d’un signal) (216)


-
24.11.2013 : Modélisation spatiale (215)

-
10.11.2013 : Minimiser / maximiser (214)

-
6.11.2013 : Approche vectorielle (213)

-
31.10.2013 : Echanger (212)

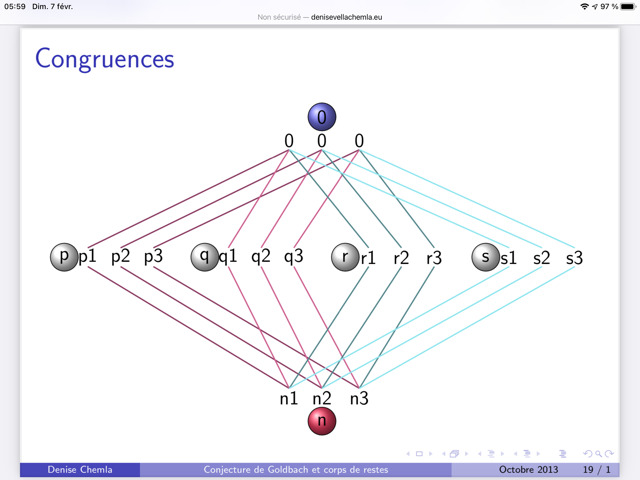 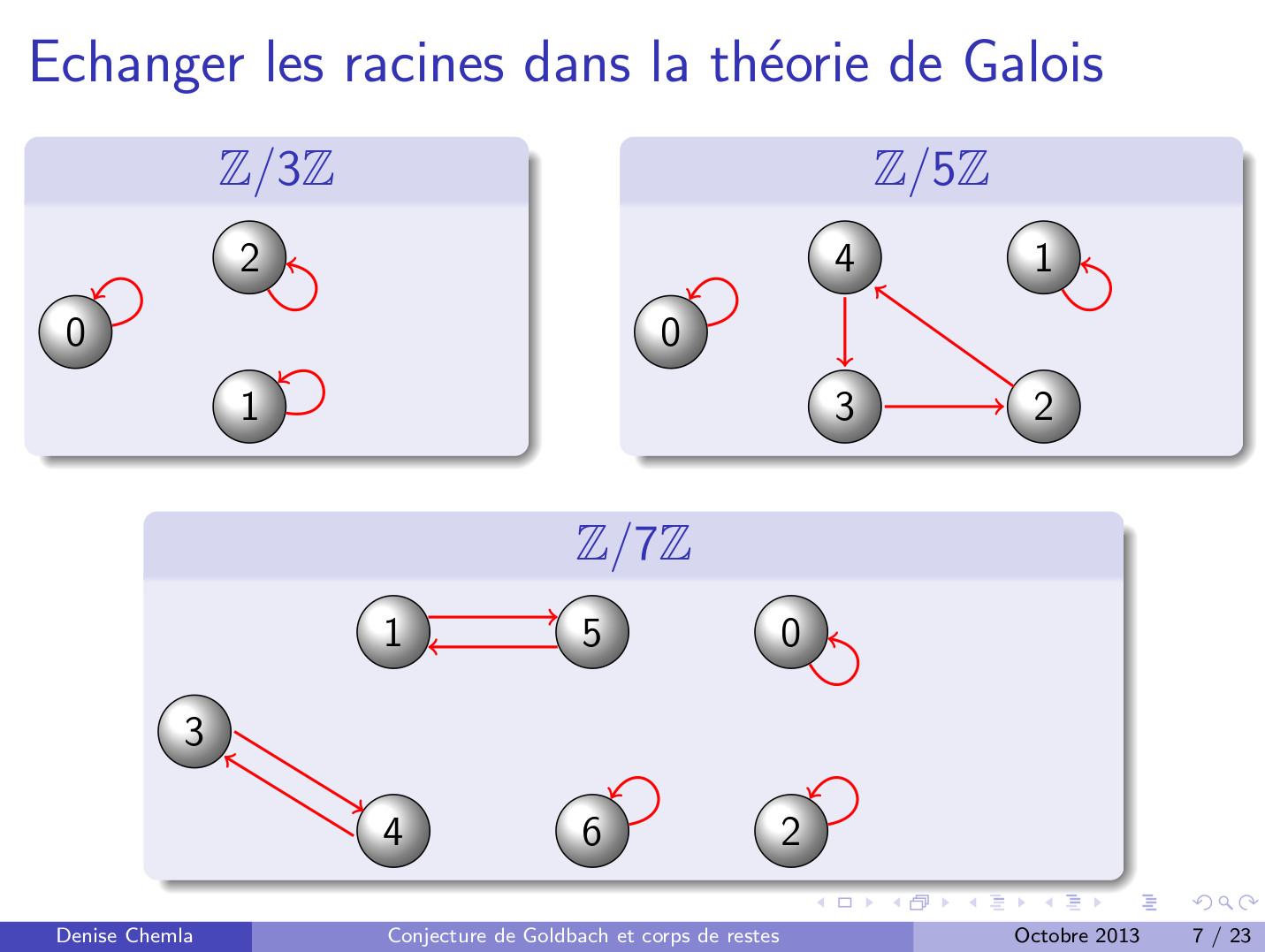
-
31.10.2013 : Note sur l’approche par le transfert d’une solution triviale (211)


-
24.10.2013 : Localisation en prose (210)

-
13.10.2013 : Dévisser des groupes (209)

-
22.9.2013 : Combinatoire de congruences (208)

-
13.9.2013 : Pistes à creuser (207)

-
24.8.2013 : Division euclidienne et conjecture de Goldbach (206)

-
10.8.2013 : Division euclidienne et
conjecture de Goldbach (205)

-
9.8.2013 : Parité... (204)

-
2.8.2013 : Brisure de symétrie (203)

-
15.7.2013 : Espace, distance, horloges (202)

-
novembre 2013 à février 2014 : S’intéresser, un peu, à la physique, notamment quantique (201)

-
2.6.2013 : Les livres délivrent. (200)


-
1.4.2013 : Minorer le nombre de décomposants de Goldbach (199)

-
16.3.2013 : Minorer le nombre de décomposants de Goldbach (198)

-
5.2.2013 : Equations polynomiales modulaires et conjecture de Goldbach (197)

-
4.2.2013 : Théorie de Galois et conjecture de Goldbach (196)

-
2.2.2013 : Expérimentations numériques à l’aide du logiciel Gap et du package associé Loops (195)

-
30.1.2013 : Théorie des groupes et Conjecture de Goldbach (remerciements à GreginGre et Archimède du forum Algèbre du site les-mathematiques.net) (194)

-
28.1.2013 : Où Galois cite la méthode de Libri pour trouver des solutions entières (p.405) (193)

-
28.1.2013 : Extrait de Libri auquel Galois fait référence (192)

-
25.1.2013 : Dessin de la bijection de Cantor (191)

-
16.1.2013 : Recherche de suites les plus longues de nombres respectant certaines contraintes, articles de Legendre et Desboves (190)

-
11.1.2013 : Minorer par le nombre de décompositions de Goldbach des doubles de nombres premiers qui vérifient trivialement la conjecture. (189)

-
8.1.2013 : Idem mais en notant les divisibilités pour la seconde passe plutôt que les congruences à n (188)

-
8.1.2013 : Le double crible, Brun y a pensé en 1919. (187)

-
5.1.2013 : Séparer les problèmes, selon Pólya : les 6m, les 6m+2, les 6m+4 (186)



-
30.12.2012 : Remettre les nombres dans l’ordre pour bien voir les récurrences, mais on ne sait toujours pas comment relier les deux colonnes... (185)

-
27.12.2012 : Desboves critique Legendre (1855) (184)

-
Noël 2012 : Diaporama : Un algorithme d’obtention des décomposants de Goldbach d’un nombre pair (183)

-
Noël 2012 : Un algorithme d’obtention des décomposants de Goldbach d’un nombre pair (182)

-
Christmas 2012 : Slides : An algorithm to obtain an even number’s Goldbach components (181)

-
Christmas 2012 : An algorithm to obtain an even number’s Goldbach components (180)

-
24.12.2012 : Un extrait du tome II de la Théorie des nombres de Legendre (179)

-
19.12.2012 : Etude de cas (178)

-
19.12.2012 : Case study (177)

-
19.12.2012 : Diaporama : Un algorithme d’obtention des décomposants de Goldbach d’un nombre pair (176)

-
19.12.2012 : Un algorithme d’obtention des décomposants de Goldbach d’un nombre pair (175)

-
19.12.2012 : Slides : An algorithm to obtain an even number’s Goldbach components (174)

-
19.12.2012 : An algorithm to obtain an even number’s Goldbach components (173)

-
4.12.2012 : Application double du crible d’Eratosthène pour trouver les décomposants de Goldbach d’un nombre pair (172)

-
4.12.2012 : Etude de cas (171)

-
1.12.2012 : Les décomposants de Goldbach de x se trouvent par application double du crible d’Eratosthène (170)

-
1.12.2012 : Chercher une démonstration par récurrence (169)

-
1.12.2012 : Les progressions arithmétiques, c’est extra ! (168)

-
10.11.2012 : (diaporama) Etude élémentaire de la conjecture de Goldbach (167)

-
7.10.2012 : Une méthode originale de David Angell pour calculer la résiduosité quadratique d’un nombre à un autre (166)

-
1.9.2012 : Méthode quasi-exhaustive (165)

-
14.7.2012 : (diaporama) Etude élémentaire de la conjecture de Goldbach (remerciements à Cyril qui m’a bien aidée à les améliorer) (164)

-
7.7.2012 : Découverte d’une loi tout extraordinaire par rapport à certaines sommes de restes des nombres premiers (163)

-
4.7.2012 : Tentative ratée de minoration probabiliste pour Goldbach (162)

-
2.7.2012 : (diaporama) Etude élémentaire de la conjecture des nombres premiers d’écart 2 (161)

-
30.6.2012 : Infinité de l’ensemble des nombres premiers d’écart 2, conjecture de Goldbach et un lemme de Gauss (article 127) (160)

-
24.6.2012 : (diaporama) Etude élémentaire de la conjecture de Goldbach (159)

-
15.6.2012 : Conjecture des nombres premiers d’écart 2, construction de nombres pairs juste entre deux nombres premiers compris entre deux primorielles successives (à revoir) (158)

-
14.6.2012 : Conjecture des nombres premiers d’écart 2 et argument d’Euclide (note reprise) (157)

-
13.6.2012 : Conjecture des nombres premiers d’écart 2 et argument d’Euclide (note) (156)

-
12.6.2012 : Conjecture des nombres premiers d’écart 2 et diagonale de Cantor (note) (155)

-
7.6.2012 : Génération de nombres premiers d’écart 2 (154)

-
6.6.2012 : Infinitude de l’ensemble des nombres premiers d’écart 2 (une idée provenant de l’exercice consistant à démontrer l’infinitude de l’ensemble des nombres premiers de la forme 6k+1) (153)

-
6.6.2012 : Versions anglaises (152)



-
23.5.2012 : Infinitude de l’ensemble des nombres premiers d’écart 2 (reprise) (151)

-
30.4.2012 : (diaporama) La piste qui me semble la bonne, depuis longtemps (150)

-
30.4.2012 : (diaporama) Les autres pistes que j’ai suivies (149)

-
30.4.2012 : (diaporama) La piste que je veux suivre
(148)

-
24.4.2012 : Retour aux congruences (147)

-
20.4.2012 : Décompositions de Goldbach et transitivité (146)

-
16.4.2012 : Lier décomposants de Goldbach et non-résidus quadratiques (145)

-
9.3.2012 : Début d’une récurrence (144)

-
♥ 1.1.2012 : Bonne année 2012... (143) (nullité déterminant matrice de Sylvester)

-
25.12.2011 : Nullité du déterminant d’une matrice de Sylvester (142)

-
11.12.2011 : Invariance de polynômes (141)

-
27.11.2011 : Algorithme combinatoire (140)

-
25.11.2011 : Compter des nombres dans des lignes (139)
-
23.11.2011 : Une vision plus algorithmique de la conjecture de Goldbach (138) (récurrence sur une seule séquence de nombres)

-
20.11.2011 : Rester éberluée face aux polynômes (137)

-
16.11.2011 : La conjecture de Goldbach est peut-être vraie à cause de la Théorie de Galois (136)

-
♥ 11.11.2011 : En attendant le 7 juin 2012 (les 270 ans de la conjecture de Goldbach), utiliser les équations algébriques pour trouver les décomposants de Goldbach... (135)

réétudié en mai 2025 :   
-
♥ 6.11.2011 : Une dernière idée : utiliser la théorie de Galois pour trouver les décomposants de Goldbach... (134)

-
♥ 31.10.2011 : Une dernière idée : utiliser la théorie de Galois pour trouver les décomposants de Goldbach... (133)

-
30.10.2011 : Conjecture de Goldbach d’un point de vue analytique (132)

-
28.10.2011 : On trouve toujours un non-résidu quadratique de n qui fournisse une décomposition de Goldbach de n (131)

-
25.10.2011 : Une nouvelle tentative pour prouver que tout nombre pair supérieur à 2 est la somme de deux nombres premiers
(où l’on repart du côté des résidus et non-résidus quadratiques) qui n’aboutit toujours pas. (130)

-
22.10.2011 : Une nouvelle tentative, utilisant le produit des unités de n, de prouver que tout nombre pair supérieur à 2 est la somme de deux nombres premiers, mais qui n’aboutit pas non plus. (129)

-
5.10.2011 : La racine carrée d’un résidu quadratique inversible de n fournit une décomposition de Goldbach de n. (128)

-
3.10.2011 : Tables de visualisation des décompositions de Goldbach, des résidus et non-résidus quadratiques de n, tous premiers à n (127)

-
3.10.2011 : Tables de visualisation des décompositions de Goldbach, des résidus et non-résidus quadratiques de n, tous premiers à n (126)

-
1.10.2011 : Quel est le nombre de résidus quadratiques de n qui sont premiers à n ? (125)

-
28.9.2011 : Il existe un non-résidu de n dont le carré modulo n est premier à n et qui fournit une décomposition de Goldbach de n. (124)

-
27.9.2011 : Bicentenaire de la naissance d’Evariste Galois, le 25.10.2011. (123)


-
27.9.2011 : Evariste Galois cite Guillaume Libri (Journal de Crelle, IX, se reporter à la page 19 du pdf - ou p. 186 du Journal - où sont présentées certaines équations ayant forcément des solutions entières). (122)

-
27.9.2011 : Evariste Galois cite Guillaume Libri (se reporter à la page 50 du pdf - ou p.44 du mémoire - pour voir ce que propose Libri pour trouver les solutions entières de certaines équations). (121)

-
18.9.2011 : Un non-résidu de tous les diviseurs impairs de n fournit une décomposition de Goldbach de n
(120)

-
7.9.2011 : Où ça devient carrément de plus en plus joli... (119)

-
2.9.2011 : Pas de fourmi et méthode Coué... (118)

-
31.8.2011 : Un article de Anne-Marie Décaillot qui présente une démonstration de la loi de réciprocité quadratique basée sur l’arithmétique des tissus de Lucas (117)

-
24.8.2011 : Conjecture de Goldbach et congruences du second degré (116)

-
22.8.2011 : La note de Cantor au Congrès de l’AFAS de Caen en 1894 (115)

-
22.8.2011 : Lettre manuscrite de Goldbach à Euler du 7 juin 1742 (114)

-
22.8.2011 : Version de Fuss de la Lettre de Goldbach à Euler (113)

-
22.8.2011 : Version de Fuss de la réponse d’Euler à Goldbach du 30 juin 1742 (112)

-
8.8.2011 : L’intellectuel de Beauval

-
20.2.2011 : Expérimentations autour des nombres de décompositions de Goldbach (partitions pour les 2^k.p) (111)

-
14.1.2011 : Poursuite des expérimentations, à la recherche d’une récurrence fournissant le nombre de décompositions de Goldbach d’un nombre pair donné (110)

-
8.1.2011 : Présentation du crible basé sur la symétrie (109)

-
7.1.2011 : Grilles d’obtention de certaines décompositions de Goldbach de 2x par symétrie autour de x (108)

-
♦♦;-) à Daniel Diaz, qui a écrit gnu-prolog. (107)

-
1.1.2011 : Comète de Goldbach et autres comètes (suite) (106)

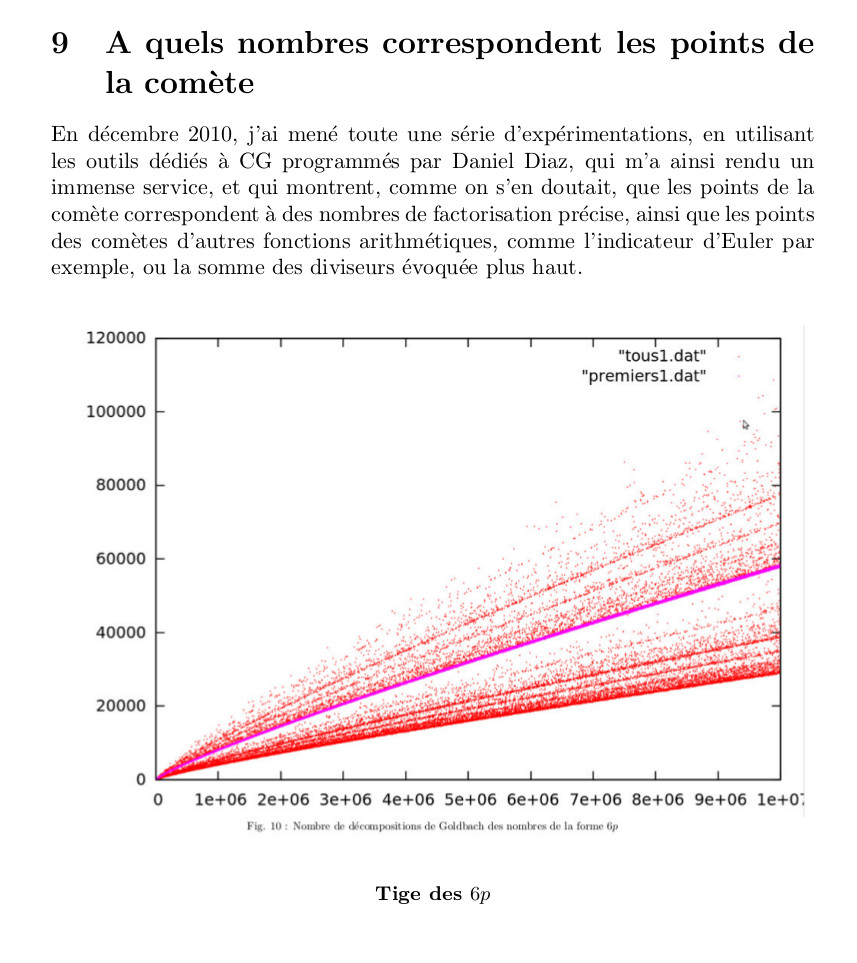 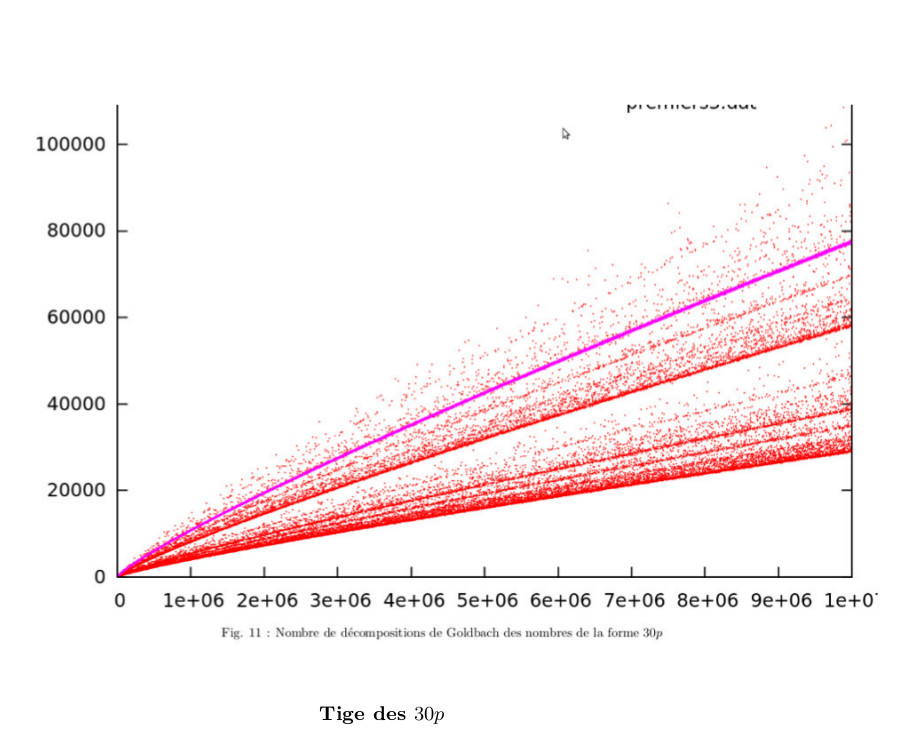 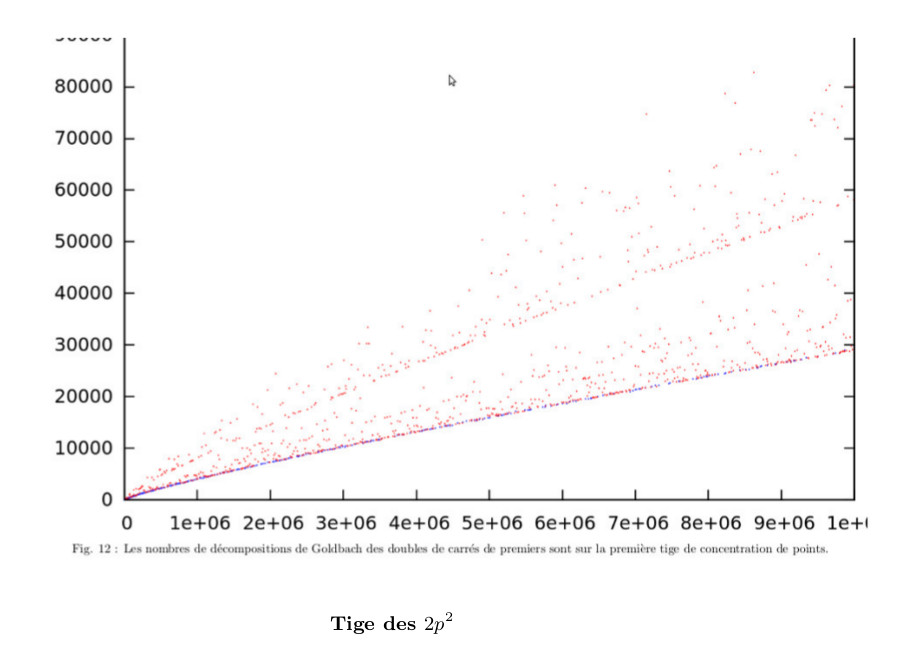
-
1.1.2011 : Comète de Goldbach et autres comètes (idem mais dessins au format paysage) (105)

-
25.12.2010 : Comète de Goldbach et autres comètes (104)

-
5.12.2010 : Des fonctions qui semblent minorer le nombre de décompositions de Goldbach d’un nombre pair 2x donné (103)

-
28.11.2010 : Note concernant une fonction qui semble minorer le nombre de décompositions de Goldbach d’un nombre pair 2x donné (102)

-
24.11.2010 : De surprise en surprise : floor(√(x)/4) semble minorer le nombre de décompositions de Goldbach d’un nombre pair 2x donné (101)
-
23.11.2010 : Une fonction simple qui semble minorer le nombre de décompositions de Goldbach d’un nombre pair donné (100)

-
11.11.2010 : Petites notes dont une fonction qui semble minorer le nombre de décompositions de Goldbach d’un nombre pair donné (99)

-
12.9.2010 : L’ensemble des nombres premiers d’écart 2 est infini (98)

-
1.5.2010 : Chercher un lien entre la conjecture de Goldbach et la Loi de réciprocité quadratique (97)

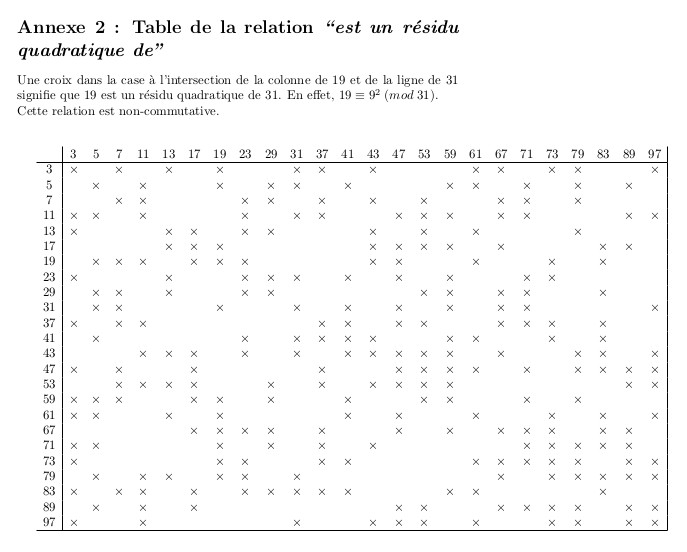  
-
11.3.2010 : Conjecture de Goldbach, Jacquard et réécriture ; il faut conserver les deux dimensions des grilles et prouver que les substitutions horizontales ont une conséquence verticale... (96)

-
8.3.2010 : Conjecture de Goldbach, Jacquard et réécriture (95)

-
1.2.2010: La fonction récursive ne permet pas de progresser (94)

-
7.8.2009 : Une fonction récursive de comptage liée à la conjecture de Goldbach (93)

-
17.6.2009 : Une fonction récursive de comptage liée à la conjecture de Goldbach (92)

-
15.6.2009 : Résumé de la méthode utilisant la fonction récursive f (91)

-
Diapositives (14.6.2009) : Une fonction récursive de comptage liée à la conjecture de Goldbach (90)

-
13.6.2009 : Introduction de la fonction récursive de comptage liée à la conjecture de Goldbach (89)

-
Diapositives (4.6.2009) : Conjecture de Goldbach et formule du crible de Poincaré (88)

-
3.6.2009 : Conjecture de Goldbach et formule du crible de Poincaré (87)

-
27.5.2009 : Conjecture de Goldbach, Conjecture des nombres premiers d’écart 2, test de primalité et sinusoïdes (86)

-
24.5.2009 : Résumé de la méthode utilisant les matrices carrées de congruence (85)

-
20.5.2009 : Valeurs absolues des résidus minima absolus de Gauss et conjecture de Goldbach (84)

-
12.5.2009 : Tester autrement la primalité (83)

-
Diapositives (10.5.2009) : Une nouvelle caractérisation des nombres premiers (82)

-
10.5.2009 : Valeurs absolues des résidus minima absolus de Gauss et conjecture de Goldbach (81)

-
9.5.2009 : Méthode de recherche des décomposants de Goldbach par les ensembles d’entiers (80)

-
Diapositives (8.5.2009) : Conjecture de Goldbach et ensembles de restes modulaires (79)

-
Diapositives (7.5.2009) : Conjecture de Goldbach et théorie des graphes (78)

-
Diapositives (3.5.2009) : Algorithme de calcul des décomposants de Goldbach utilisant des mots binaires (77)

-
1.5.2009 : Des formulations équivalentes de la conjecture de Goldbach (approche par la théorie des langages, la théorie des graphes, la théorie des ensembles) (76)

-
27.4.2009 : Piste pour une démonstration de la conjecture de Goldbach (75)

-
26.4.2009 : Conjecture de Goldbach et mots binaires (74)

-
26.4.2009 : Reformulation de la conjecture de Goldbach dans le domaine de la combinatoire des mots (73)

-
25.4.2009 : Conjecture de Goldbach et affectation de mots binaires (72)

-
25.4.2009 : Où l’on plie des tissus (71)

-
22.4.2009 : Etude graphique de la conjecture de Goldbach (70)

-
18.4.2009 : Vision géométrique de la conjecture de Goldbach (69)

-
16.4.2009 : Etude combinatoire de la conjecture de Goldbach (68)

-
14.4.2009 : Arithmétique des tissus et conjecture de Goldbach (67)

-
1.4.2009 : Conjecture de Goldbach et suite de mots binaires (66)

-
Diapositives (24.3.2009) : Treillis d’ensembles de nombres (65)

-
23.3.2009 : Polynômes caractéristiques de matrices de congruence (64)

-
Diapositives (21.3.2009) : Etude de la conjecture de Goldbach utilisant les restes modulaires (63)

-
Programmation de la méthode par les valeurs absolues des résidus modulaires minima de Gauss (62)

-
Idée enfantine de Gauss (61)

-
Tout écrit est un appel. (60)

-
Matrices carrées de booléens vues comme des matrices d’incidence de graphes (59)

-
Programmation de la méthode de recherche des décomposants de Goldbach utilisant des mots binaires (un décomposant de Goldbach d’un entier lui permet de vérifier la conjecture de Goldbach) (58)

-
Programmation de l’algorithme de calcul des mots associés à un nombre pair (57)

-
Théorie des langages, combinatoire des mots (56)

-
Etudier la conjecture de Goldbach en utilisant les probabilités (55)

-
Galois (54)

-
Décompositions de Goldbach des premiers entiers (qui leur permet de vérifier la conjecture de Goldbach) (53)

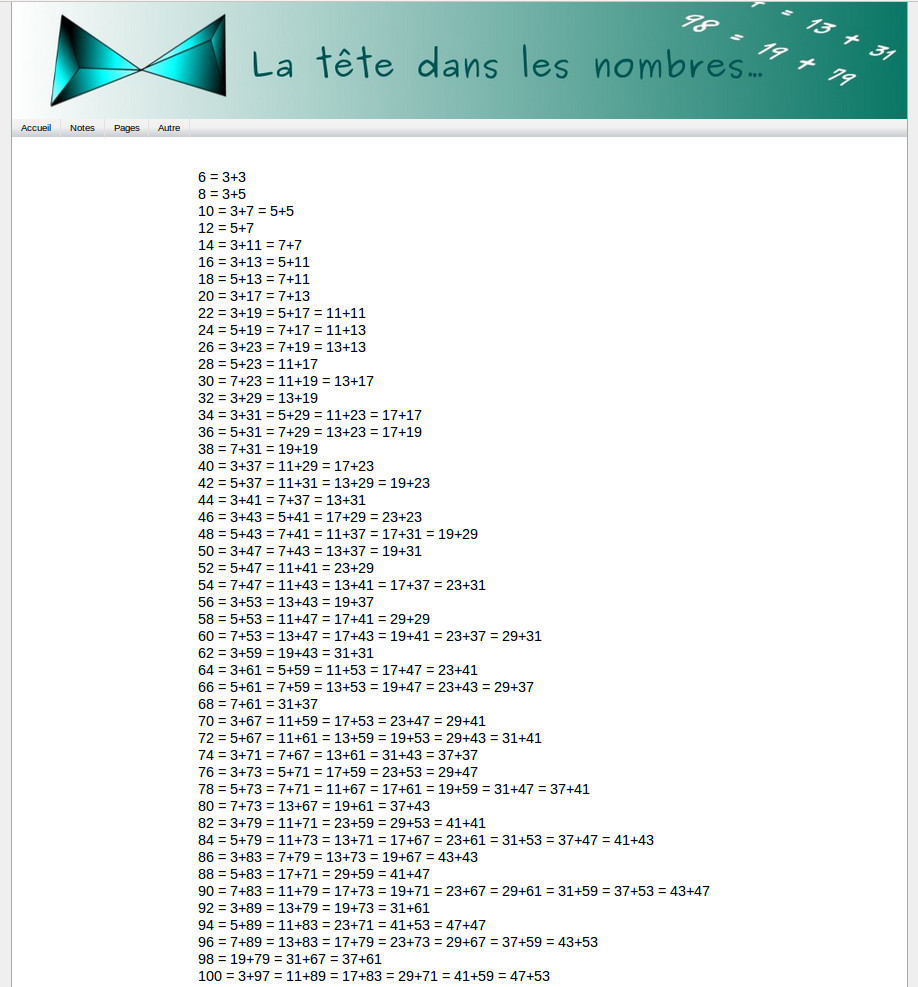
-
Ma conjecture : 2x (supérieur à 12) partage toujours l’un de ses décomposants de Goldbach avec 2x-6 (et vérifie ainsi la conjecture de Goldbach) (52)


-
Associer à chaque entier un ensemble de fractions rationnelles et caractériser autrement la primalité (51)

-
Hilbert et Cantor (50)

-
Revenir à la division euclidienne (49)

-
Empilement de valuations p-adiques et TNP (Théorème des Nombres Premiers) (48)

-
Enoncé de la conjecture de Goldbach (47)

-
Divisibilité des factorielles (Lucas) (46)

-
♥♥ Fractales (45)

-
Démonstration constructive ou non, fenêtre de recherche d’un décomposant de Goldbach d’un entier (lui permettant de vérifier la conjecture de Goldbach) (44)

-
Géométrie des nombres de Minkowski, équations de droites, théorème de Noël (43)

-
Conjecture de Goldbach et Théorie des graphes (à arêtes colorées, cf Ramsey) (42)

-
Groupe cyclique des unités (41)

-
Incongruences (dessin des ensembles) (40)

-
Indicateur d’Euler (39)

-
Crible de Matiiassevitch (38)

-
Moyennes arithmétiques (densité du photon !) (37)

-
Rencontre de la non-commutativité, à minuscule échelle (36)

-
Okounkov (35)

-
Merveilleux polyèdres (34)

-
Racines de polynomes, Congruence des sommes de racines (33)

-
Primorielles (32)


-
Théorème des quatre carrés de Lagrange (31)

-
La loi de réciprocité quadratique de Gauss (30)

-
Un beau maillage (29)

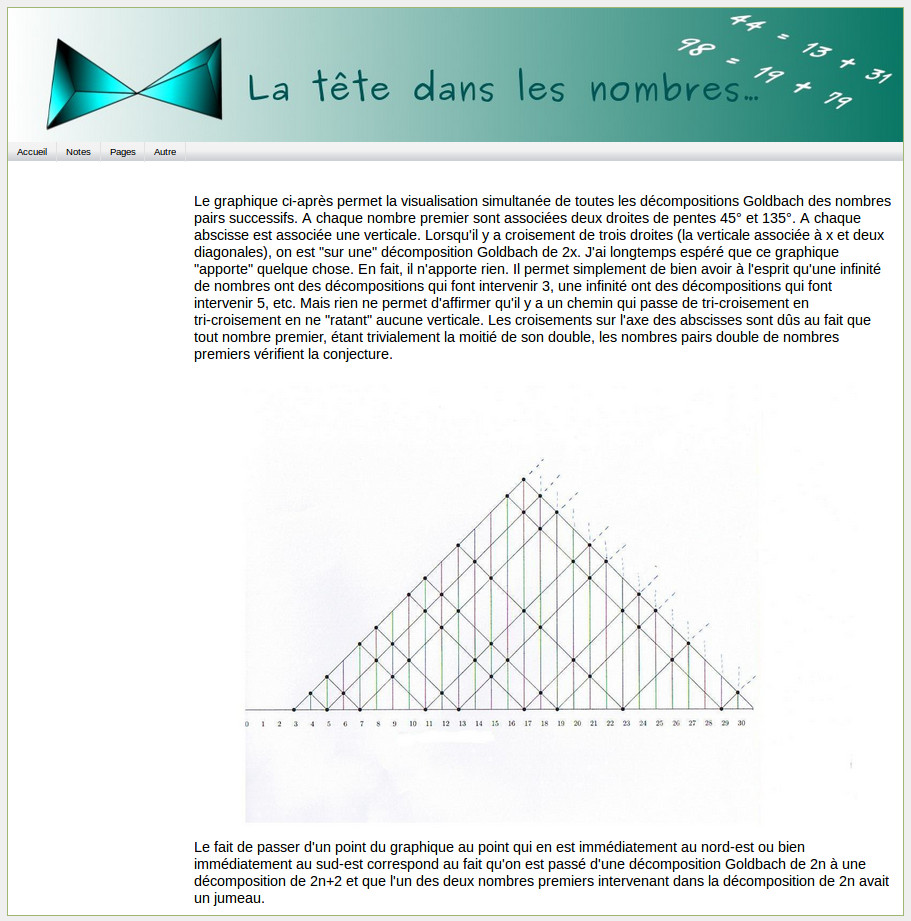
-
Démonstration par récurrence, réglettes de Laisant (28)

-
Index

-
1.3.2009 : Matrices de congruence et descente infinie (27)

-
27.2.2009 : Utiliser les probabilités pour étudier la conjecture de Goldbach (26)

-
22.11.2008 : Congruences, combinaisons linéaires (25)

-
1.11.2008 : Approches algébrique et géométrique de la conjecture de Goldbach (24)

-
12.5.2008 : Partage des décomposants de Goldbach (ou bien pour ceux que ça transporte de voir 123321 sur le compteur kilométrique) (23)

-
31.3.2008 : Prendre la tangente (22)

-
9.1.2008 : Petites notes (21) (Sharol Nau
 ) )

-
1.11.2007 : Détermination des décomposants de Goldbach grâce au théorème des restes chinois (20)

-
1.10.2007 : Changer l’ordre sur les entiers naturels pour comprendre le partage des décomposants de Goldbach (19)

-
1.7.2007 : Arbres de nombres et conjecture de Goldbach (18)

-
1.1.2007 : Une nouvelle façon de voir les nombres premiers (17)

-
1.1.2007 : Conjecture de Goldbach et propriétés de symétrie d’une table de congruence (16)

-
1.1.2007 : Une approche enfantine des nombres premiers (15)

-
25.12.2006 : Conjecture de Goldbach et symétrie dans les tables de congruence (14)

-
1.11.2006 : Résultats trouvés sur différents groupes avec l’outil GAP (13)

-
1.10.2006 : Conjecture de Goldbach et théorie des groupes (12)

-
1.9.2006 : Esthétique des décompositions de Goldbach de certains nombres pairs (11)

-
1.8.2006 : Conjecture de Goldbach et polynômes symétriques (10)

-
1.6.2006 : Sous-graphe d’ordre maximal d’un graphe coloré (9)

-
3.5.2006 : Factorisation des factorielles, ensembles et relations (8)

-
1.5.2006 : Représentation de la combinatoire associée à la conjecture de Goldbach par des graphes (7)

-
♥♥ 1.2.2006 : Fractales, symétrie et conjecture de Goldbach (6)

    
-
1.1.2006 : Lien conjecture de Goldbach / indicateur d’Euler (5)

-
1.12.2005 : Vers une preuve de la conjecture de Goldbach (4)

-
1.11.2005 : Vers une preuve de la conjecture de Goldbach (3)

-
1.10.2005 : Extraits des Recherches arithmétiques de Gauss
-
1.10.2005 : Vers une preuve de la conjecture de Goldbach (2)

-
1994 : un seul article publié, présenté à ILPS’94 (International Logic Programming Symposium, Ithaca, New-York), coécrit avec Daniel Diaz, Serge Manchon, Philippe Kerlirzin, lors d’une mission SYSECA au CENA (Centre d’Etudes de la Navigation Aérienne) Using CLP(FD) to solve Air Traffic Flow Management (1)

-
Compilations : cliquer sur les titres de la (ou des) page(s) de garde pour aller directement sur les notes ;
2005 à 2008  2009 à 2010 2009 à 2010  2011 2011  2012 (avant oct.) 2012 (avant oct.)  nov. 2012 à juil. 2013 nov. 2012 à juil. 2013  juil. 2013 à avr. 2014 juil. 2013 à avr. 2014  avr. à oct. 2014 avr. à oct. 2014  2015 2015  2016 2016  2017 2017  2018 2018  2019 2019  Chouettes souvenirs Chouettes souvenirs  juin 2019-juin 2020 juin 2019-juin 2020  2020 transc-trad-LaTex 2020 transc-trad-LaTex   2020 recherches 2020 recherches  2021 2021  2022 2022  2023 2023  2024 2024 
-
"Sourire, sourire, toujours sourire, même si l’on te traite de p’tit laid..." (Claude Nougaro)
|