|
On peut partir dans deux directions pour représenter la conjecture de Goldbach en utilisant la théorie des graphes :
1) On peut utiliser un graphe biparti dont les deux ensembles de sommets sont d'une part l'ensemble des nombres premiers impairs inférieurs à x, qu'on appellera les 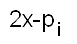 (on cherche l'existence de décompositions Goldbach pour 2x pair), d'autre part, l'ensemble des nombres de la forme  .Il y a une arête entre deux sommets lorsqu'ils sont liés par une relation de divisibilité. Exemples :
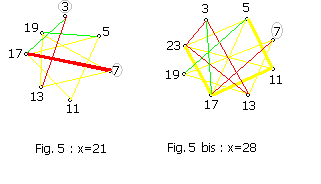
On comprend qu'il y a autant de décompositions Goldbach pour un nombre pair que de sommets dans l'ensemble de droite n'étant relié à aucune arête. Pour prouver la conjecture, il faudrait être capable de montrer qu'un tel sommet non relié à une arête existe forcément. Ou bien être capable de prouver que l'existence d'au moins une arête associée à chaque sommet de droite permet d'aboutir à une contradiction. 2) La contradiction qu'on essaie d'établir ci-dessus nous oblige à prendre en compte les écarts entre les nombres premiers (qui sont d'ailleurs identiques dans les deux ensembles du graphe biparti puisque 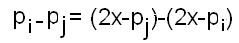 ).Du coup, on s'intéresse au graphe complet (tout sommet est relié à tout sommet) dont les sommets sont les nombres premiers inférieurs à x. On va relier les sommets par des arêtes colorées (il faut une couleur pour chaque nombre premier) selon que l'écart qui les sépare est divisible par tel ou tel nombre premier. Par exemple, dans le graphe complet suivant, la couleur noire correspond à un écart entre les sommets divisible par 2, la couleur rouge correspond à un écart entre les sommets divisible par 3, et la couleur jaune à un écart divisible par 5.
Tous les sommets qui ne divisent pas x et qui ne sont pas touchés par un arc épaissi permettent de trouver une décomposition Goldbach de 2x. Problème : ces graphes plein de sommets, d'arcs et de couleurs sont vite absolument illisibles et difficiles à étudier. Ci-dessous, les graphes correspondant aux minuscules nombres pairs (!) 42 et 56. A l'adresse http://fr.wikipedia.org/wiki/Théorie_de_Ramsey sont fournis trois théorèmes de la théorie de Ramsey qui concernent les coloriages de graphes qui pourraient peut-être être utilisés ici...
|
