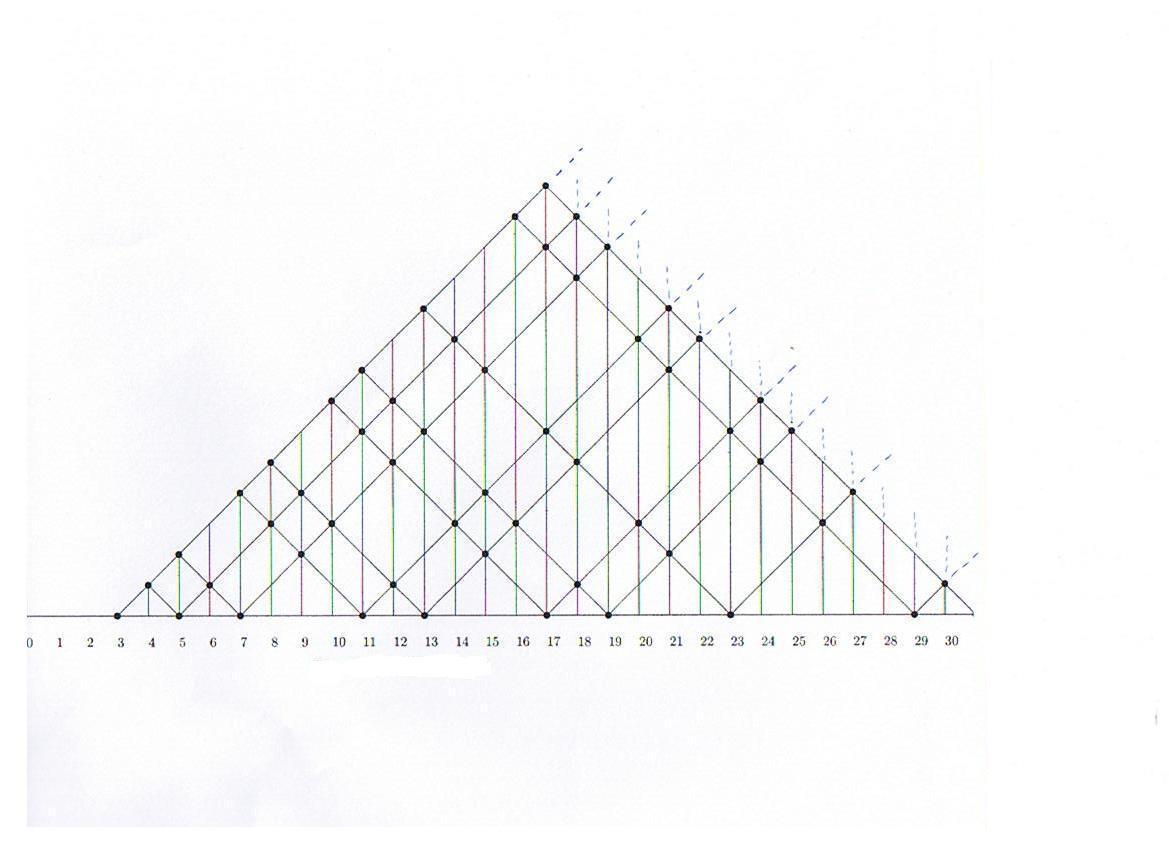
Le graphique ci-après permet la visualisation simultanée de toutes les décompositions Goldbach des nombres pairs successifs. A chaque nombre premier sont associées deux droites de pentes 45° et 135°. A chaque abscisse est associée une verticale. Lorsqu'il y a croisement de trois droites (la verticale associée à x et deux diagonales), on est "sur une" décomposition Goldbach de 2x. J'ai longtemps espéré que ce graphique "apporte" quelque chose. En fait, il n'apporte rien. Il permet simplement de bien avoir à l'esprit qu'une infinité de nombres ont des décompositions qui font intervenir 3, une infinité ont des décompositions qui font intervenir 5, etc. Mais rien ne permet d'affirmer qu'il y a un chemin qui passe de tri-croisement en tri-croisement en ne "ratant" aucune verticale. Les croisements sur l'axe des abscisses sont dûs au fait que tout nombre premier, étant trivialement la moitié de son double, les nombres pairs double de nombres premiers vérifient la conjecture. Le fait de passer d'un point du graphique au point qui en est immédiatement au nord-est ou bien immédiatement au sud-est correspond au fait qu'on est passé d'une décomposition Goldbach de 2n à une décomposition de 2n+2 et que l'un des deux nombres premiers intervenant dans la décomposition de 2n avait un jumeau.