|
Dans une lettre à Euler du 7 juin 1742, Goldbach énonce : "il semble que tout nombre entier supérieur à 2 soit la somme de trois nombres premiers". Euler reformule cette conjecture en une forme équivalente : "tout nombre pair supérieur à 2 est la somme de deux nombres premiers".
Un énoncé équivalent de la conjecture est que tout nombre supérieur ou égal à 2 est la moyenne de deux nombres premiers (ou bien est à égale distance de deux nombres premiers). Enfin, on peut dire qu'il s'agit de démontrer que l'application qui à toute paire de nombres premiers impairs associe leur moyenne arithmétique (qui est un entier naturel supérieur ou égal à 6) est une application surjective. J'ai souvent cherché à aboutir à une contradiction en démarrant de l'hypothèse que tous les 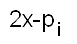 ( premier impair inférieur à x) étaient composés. On pourrait imaginer que la contradiction provienne du fait que si un certain nombre ne vérifiait pas la conjecture, un nombre plus petit ne la vérifierait pas non plus (c'est le principe de raisonnement qu'on appelle "descente infinie" inventé par Fermat)...
|