|
On va présenter ici une dernière façon de caractériser les nombres premiers, qui repose sur la manière dont Gauss enfant a associé les entiers deux à deux pour découvrir la formule
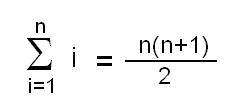
On avait pris pour habitude de considérer comme premier un nombre qui entretenait une certaine relation (être divisible par) avec d'autres nombres. Mais ce qui est également extraordinaire, c'est de voir la primalité d'un nombre comme le fait qu'il établit des relations d'indivisibilité entre des nombres inférieurs à lui pris deux à deux. Dans un premier temps, illustrons cela par des exemples. Chacun des tableaux suivants est associé à un nombre entier, qui est le résultat de la somme des deux nombres d'une même colonne. Ce nombre est premier lorsque dans chaque colonne du tableau, le nombre de la première ligne ne divise pas celui de la deuxième ligne. Si au contraire, dans une colonne au moins, le nombre de la première ligne divise celui de la deuxième, alors on a affaire au tableau d'un nombre composé. Tableau du nombre premier 5 :
Si on adopte une approche basée sur les fractions rationnelles (dont le numérateur appartient à la liste d'entiers croissants de la première ligne des tableaux) et dont le dénominateur appartient à la liste d'entiers décroissants de la deuxième ligne des tableaux), alors dans l'ensemble de fractions rationnelles associé à un entier impair, toute fraction dont le numérateur est un diviseur de ce nombre est entière. Il résulte de tout cela une nouvelle caractérisation des nombres premiers qui est : 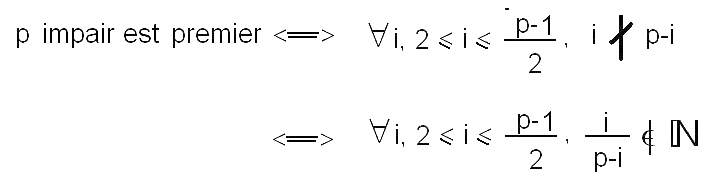 Voyons les différentes décompositions du nombre pair 40 pour étudier, grâce à cette nouvelle manière de considérer la primalité des nombres, les décompositions qui sont des décompositions Goldbach (mettant en jeu deux nombres premiers). décomposition 3 premier et 37 premier :
décomposition 5 premier et 35 composé :
décomposition 7 premier et 33 composé :
décomposition 9 composé et 31 premier :
décomposition 11 premier et 29 premier :
décomposition 13 premier et 27 composé :
décomposition 15 composé et 25 composé :
décomposition 17 premier et 23 premier :
décomposition 19 premier et 21 composé :
La formule d'existence de décomposants Goldbach pour un nombre pair qui résulte de cette approche devient : 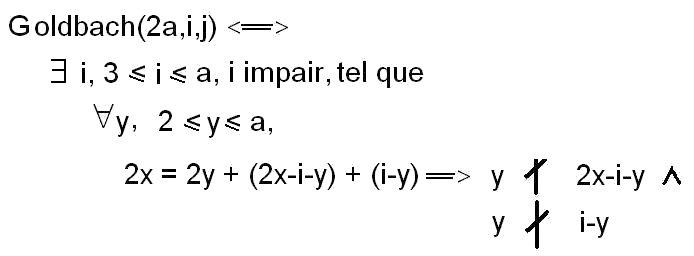
Le fichier nieme.pdf est la note correspondant à la présente page. |