Tout récemment (le 15 janvier 2007), les propriétés de symétrie découvertes dans les tables de congruence m'ont permis de trouver une nouvelle manière de caractériser les nombres premiers, qui est basée sur le fait que l'on peut associer à chaque entier impair un certain ensemble de fractions rationnelles. Le nombre considéré est premier si aucune fraction de l'ensemble n'est une fraction entière. Derrière le lien ci-dessous, nversprodq.pdf, on présente les ensembles de fractions rationnelles qu'il faut associer aux nombres de 9 à 45. Dans l'ensemble associé à un entier impair, toute fraction rationnelle dont le dénominateur est un diviseur de ce nombre est entière. Il en résulte une nouvelle caractérisation des nombres premiers qui est : 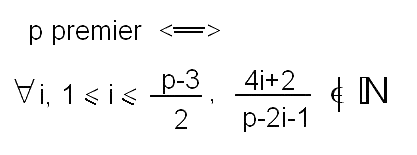On peut encore améliorer cette caractérisation car si le numérateur d'une fraction est strictement inférieur à son dénominateur, elle ne peut être entière, ce qui est le cas dès que 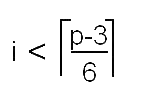On se restreint donc finalement à la caractérisation suivante : L'explication de la façon dont on a abouti à cette cette nouvelle approche est expliqué ici : premiers.pdf