|
Dans un article de vulgarisation du travail d’Okounkov, on trouve, entre autres multiples choses, un lien qu’il établit entre les groupes symétriques et les partitions d’entiers.
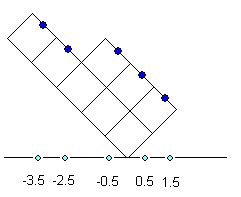
Dans la lettre de Goldbach à Euler, il y a les égalités suivantes : 4 = 1+1+1+1 = 1+1+2 = 1+3 5 = 2+3 = 1+1+3 = 1+1+1+2 = 1+1+1+1+1 6 = 1+5 = 1+2+3 = 1+1+1+3 = 1+1+1+1+2 = 1+1+1+1+1+1 1 est considéré par Goldbach comme un nombre premier (ce qui n’est pas le cas habituellement) et il explique là que pour tout nombre, on peut trouver une décomposition en le nombre de nombres premiers qu’on souhaite de la manière expliquée. Okounkov représente les partitions d’entiers par leur diagramme de Young, qu’il "fait tourner" de 135° par rapport à la façon dont on les note habituellement, les dessinant ainsi "sur la pointe". A chaque partition est associé une sorte de phénotype, qui est l’ensemble des points que certains points du diagramme projettent sur l’axe des abscisses. En ce qui concerne la conjecture, on ne s’intéresse qu’à des partitions en deux nombres seulement et qui en plus sont premiers. Puisque l’article explique qu’il y a autant de partitions possibles pour un entier donné que de représentations irréductibles du groupe symétrique d’ordre cet entier, prouver la conjecture consisterait à prouver qu’un groupe symétrique S(2x) a forcément une représentation irréductible qui se termine par 3/2, qui est de longueur p1 première et qui contient un nombre premier p2 de nombres supérieurs ou égaux à -1/2. Pour ma part, je préfère tout décaler d’1/2 à droite, ça me semble plus lisible, mais il doit sûrement y avoir une raison pour qu’Okounkov "accroche les pointes à 0" ! Ci-dessous, la représentation "à la Okounkov" de la partition 3+5 de 8.
|