|
Yuri Matiiassevitch a prouvé que le dixième problème de Hilbert n'a pas de solution. Il a également inventé un crible qui permet de distinguer aisément les nombres premiers des nombres composés.
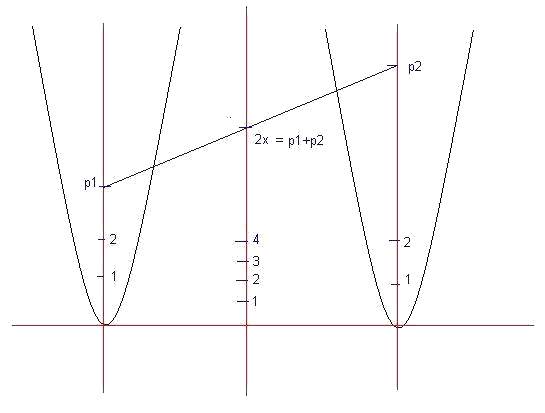
On peut trouver ce crible à l'adresse suivante : http://logic.pdmi.ras.ru/~yumat/Journal/Sieve/Sieve.html On peut similairement imaginer un "crible additif" qui calcule la somme de deux nombres. En combinant les deux idées, on peut imaginer de représenter graphiquement la conjecture de la façon suivante : sur l'axe des ordonnées gradué selon une certaine unité, on place un nombre pair 2x. On peut toujours trouver pour lui deux nombres premiers qui sont sur des axes positionnés à deux abscisses opposées dont il est la somme (ils sont tous les trois alignés). Le fait que les deux nombres soient premiers se lit par le fait qu'ils ne sont alignés ni l'un ni l'autre avec deux carrés dans leur crible de Matiassevitch respectifs.
|