|
En février 2006, j'ai écrit une note Fractales, symétries et conjecture de Goldbach : elle présentait la suite des nombres premiers comme une séquence fractale d'entiers.
En résumé, on s'intéresse à la séquence des valuations 2-adiques des nombres entiers successifs (l'exposant de la puissance de 2 dans leur décomposition). On la représente sur le graphique suivant : 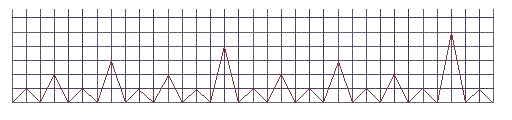
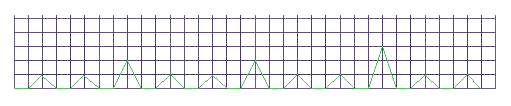 Cette séquence peut s'obtenir récursivement de la façon suivante : - la séquence initiale est "01". - pour passer de la séquence d'un niveau n à la séquence du niveau n+1, concaténer deux séquences de niveau n et changer le dernier chiffre en son successeur. On obtient 01 puis 0102 puis 01020103 puis 0102010301020104, etc... De la même façon, on obtient la séquence des valuations 3-adiques, puis 5-adiques, puis 7-adiques, etc... La procédure récursive d'obtention de la séquence de niveau n+1 nécessite simplement alors de concaténer 3, ou 5, ou 7 séquences pour passer d'un niveau au niveau supérieur. Ces séquences sont appelées séquences fractales d'entiers (cf Mandelbrot, Kimberling) parce qu'elles s'"auto-contiennent". Si on enlève tous les zéros de la séquence des valuations 2-adiques, et qu'on retranche 1 aux éléments restants, on retrouve la séquence initiale. Avant Mandelbrot, Peano, Sierpinski ou Hilbert avait inventé des courbes fractales, capables de recouvrir le plan (ça n'était d'ailleurs pas sans poser problème que le plan et la ligne se retrouve de même dimension en quelque sorte, ces courbes ont même été qualifiées de "monstruosités"). Considérons la séquence obtenue en additionnant les éléments des i séquences p-adiques associées à tous les nombres premiers Maintenant, raisonnons plus simplement, en considérant des booléens au lieu des valuations p-adiques. Je veux ajouter 01 à 001. J'ajoute (je fais un "ou" booléen) 010101 à 001001. J'obtiens la séquence 011101 de longueur 6 (=2x3). Dans cette séquence, on voit que 5 est premier (ni divisible par 2 ni par 3). Je réitère le processus avec le nouveau nombre premier obtenu 5 : je dois ajouter 011101 à 00001. J'obtiens par addition de : 011101 011101 011101 011101 011101 à 00001 00001 00001 00001 00001 00001 la séquence de longueur 30 (=2x3x5) 011111011101011101011101111101 Dans cette séquence symétrique autour de 15, je vois simultanément que 7, 11, 13, 17, 19, 23 et 29 sont premiers. 13 et 17 sont symétriques autour de 15, 11 et 19 sont symétriques autour de 15, 7 et 23 sont symétriques autour de 15. Dans ce cas, tous les nombres premiers apparaissent en même temps car on est dans le cas "chanceux" où la racine de 30 est inférieur ou égale à 6 qui est le nombre juste au-dessus du dernier nombre premier considéré 5. A la passe suivante, 2x3x5x7 = 210 mais la racine carrée de 210 est bien supérieure à 7+1, et donc les symétriques autour de 105 auront seulement les mêmes propriétés de divisibilité par 2,3,5 ou 7 mais ne seront pas forcément systématiquement premiers 2 par 2. C'est un peu comme si au fur et à mesure qu'une structure était en train de se construire, quelque chose venait la modifier pendant le cours de sa construction. Ce qui peut être intéressant concernant la conjecture de Goldbach, c'est que les séquences de valuations p-adiques (comme les séquences de booléens ci-dessus) contiennent des sous-séquences "palindromes" (présentant une symétrie-miroir autour de leur élément médian) qui sont forcément centrées sur des éléments de valuation p-adique non nulle et que cette propriété semble se transférer aux sommes de séquences. Les graphiques correspondant aux valuations p-adiques ci-dessus ressemblent un peu à des électrocardiogrammes. Il faudrait réussir à prouver que les 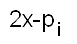 (à droite de x) ne peuvent pas tous se retrouver en haut des pics ; l'un d'entre eux doit forcément se retrouver dans des trous et ce, dans toutes les séquences des (à droite de x) ne peuvent pas tous se retrouver en haut des pics ; l'un d'entre eux doit forcément se retrouver dans des trous et ce, dans toutes les séquences des Au début, je pensais que la conjecture "tout nombre pair est la somme de deux nombres premiers" était un cas restreint d'un énoncé plus général tel que "tout multiple de k (au lieu de tout nombre pair) est la somme de k (au lieu de 2) nombres premiers". Les éléments présentés ci-dessus concernant les valuations p-adiques semblent au contraire indiquer que la conjecture est la généralisation d'énoncés plus contraints, chaque énoncé concernant un nombre premier seulement. Enfin, une anecdote : un jour, un enfant me proposa de me "montrer l'infini"... Il sortit un miroir de sa poche et le plaça face à un miroir accroché au mur. La suite de miroirs de plus en plus petits semblait ne jamais s'arrêter et l'enfant était émerveillé. La découverte de toutes ces symétries-miroir dans les séquences d'entiers est aussi fascinante. On pourra lire à ce propos les éléments de bibliographie concernant les "symétries dans la nature" et les "fractales dans la nature". Une symétrie-miroir naturelle (village de La Roche en Rame).  Une symétrie-miroir naturelle dans un fjord de Norvège (voyez-vous, l'eau d'un fjord de Norvège, quand on s'y trempe, je peux vous assurer qu'on la trouve froide, mais ce n'est pas sa fraîcheur qui coupe le souffle, c'est la beauté du paysage alentour).   Une superbe photo de symétrie-miroir prise par les personnes recensant le patrimoine (Le Cyclop de Jean Tinguely à Milly-la-Forêt).  Une superbe photo de symétrie-miroir empruntée à un article de Pierre de la Harpe pour le site Images des mathématiques.  |