Notes tamisées (toutes les notes se trouvent dans la page  ). ).
-
7 août 2025 : carrés écossais et points fixes dans le plan complexe
 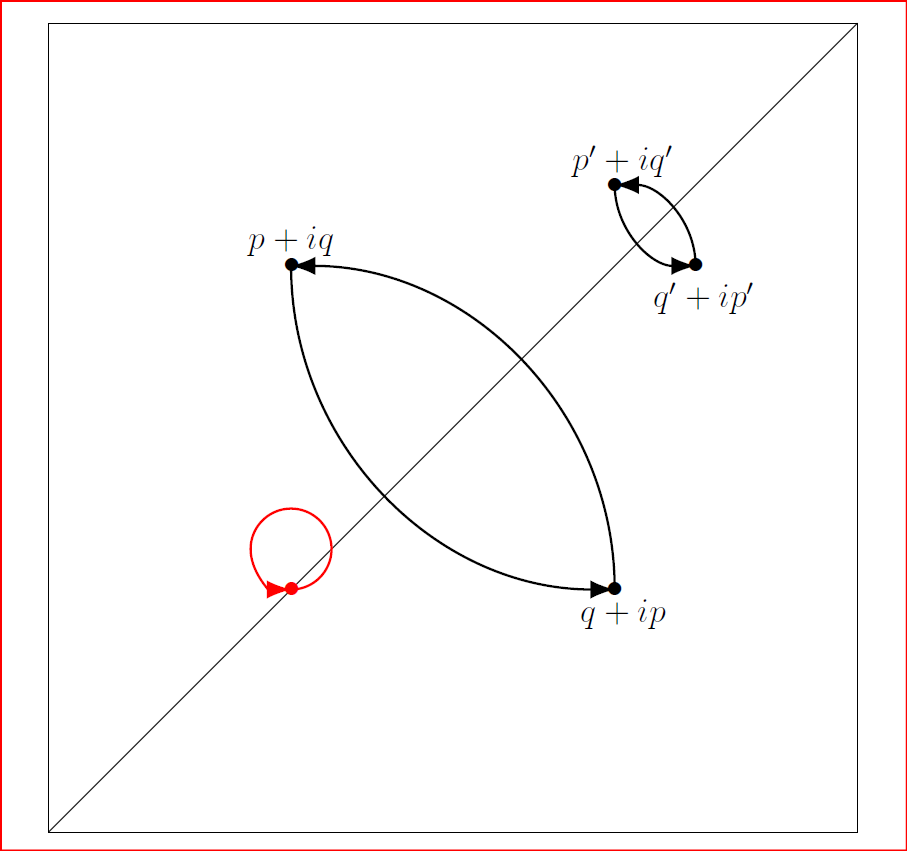
-
2025 : Matrices de booléens de divisibilité, invariance, symétrie
 2025 : Une matrice qui grandit et fournit des décompositions de Goldbach
2025 : Une matrice qui grandit et fournit des décompositions de Goldbach 
2025 : Conjecture de Goldbach, matrices booléennes, symétries 
-
2025 : Revenir aux équations algébriques
 programmation du test du déterminant de la matrice de Sylvester des deux polynômes à considérer pour Goldbach (et son résultat)
programmation du test du déterminant de la matrice de Sylvester des deux polynômes à considérer pour Goldbach (et son résultat)    
-
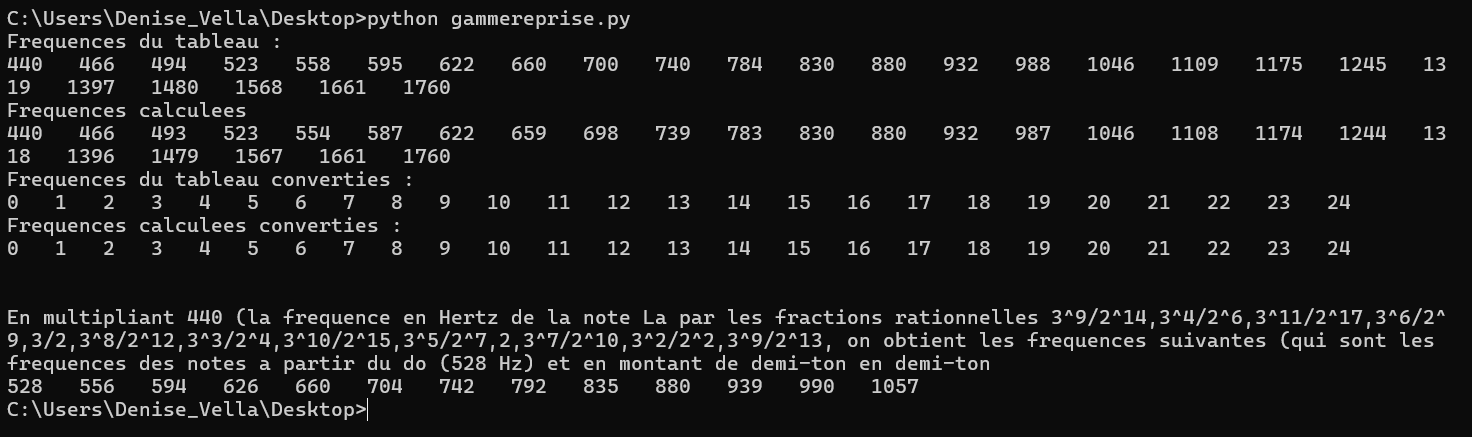
2025 : musique : conversion fréquences des notes, nombres entiers (origine la = 440 Hertz)
-
2024 : Fonction des zéros vers des réels dont les parties entières sont quasi-successives

-
2024 : résumé des résultats dans le plan complexe

-
2024 : démonstration d’une découverte qu’on avait faite en février 2024, au sujet de la somme des inverses des racines carrées des nombres entiers positifs
 essayer d'approximer des sommes d'inverses essayer d'approximer des sommes d'inverses  (la note initiale (la note initiale  ) )
-
2024 : qui utilise des automorphismes intérieurs sans en avoir conscience

-
2024 : opérateurs matriciels pour conjecture de Goldbach
 revenir à la démonstration du théorème de Morley
revenir à la démonstration du théorème de Morley 
2019 : Une application de la démonstration d’Alain Connes du théorème de Morley, à ℤ/13ℤ ou au corps des quaternions, qui contient une racine cubique de l’unité   . .
Programme Python pour preuve du théorème de Morley par Alain Connes à l’été 2020 
2025 : les 732 vérifications sur 2 millions et quelques que le théorème de Morley s'appliquent bien dans le corps ℤ/13ℤ qui contient une racine cubique de l'unité 
-
2024 : exponentielle et logarithme : Des intérêts composés (petit encart devoir d’Évariste, et dédicace spéciale à grand-papa Lulu, qui m’a appris à factoriser, et le célèbre holorime aussi)
 étonnement constant étonnement constant  Compléments par Pierre de la Harpe Compléments par Pierre de la Harpe  de ce fait, image du résultat d'un programme python d'expression du log par une racine "beaucoup"-ième de ce fait, image du résultat d'un programme python d'expression du log par une racine "beaucoup"-ième    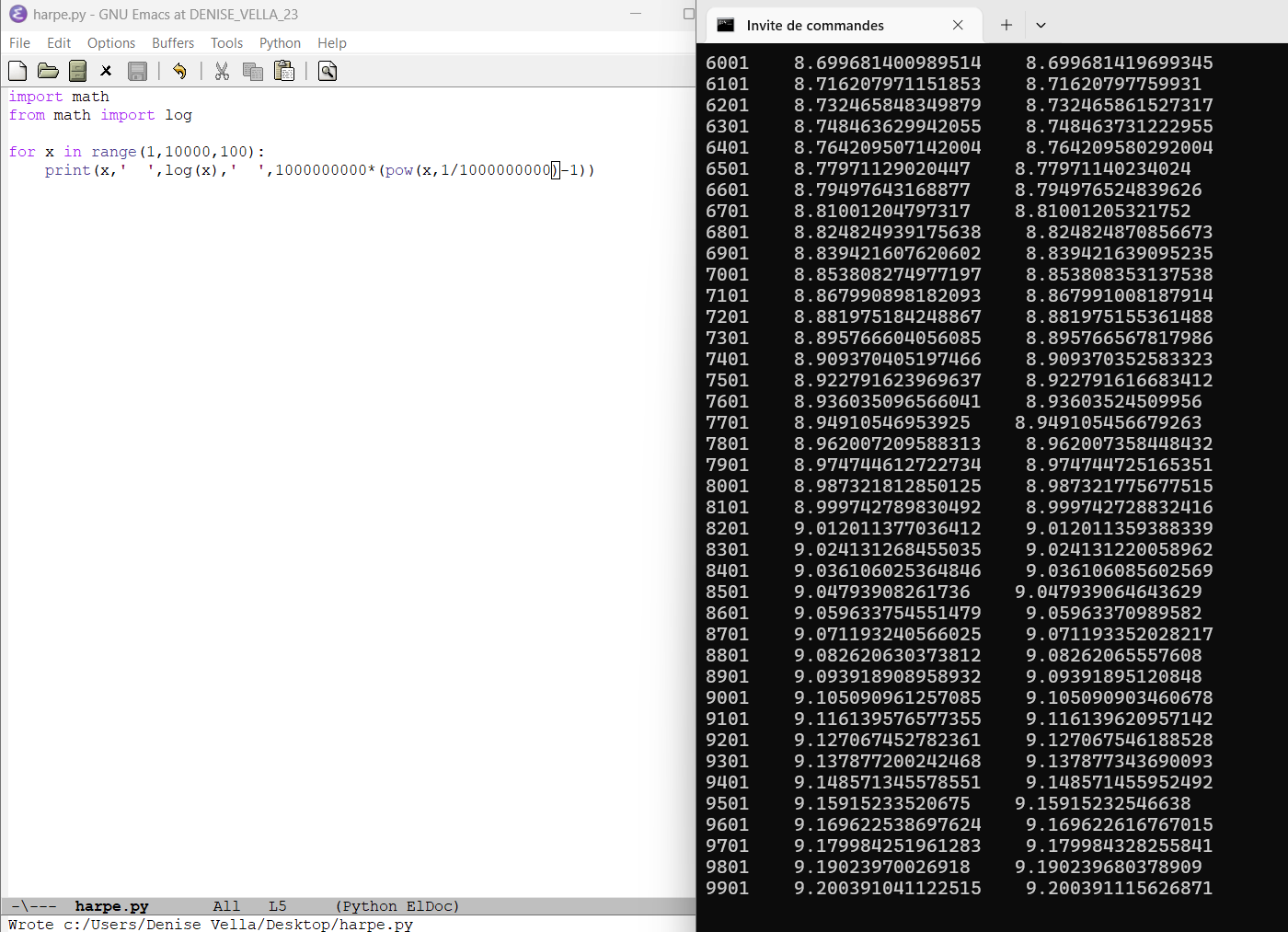
-
2024 : Snurpf et plan complexe
 compléments compléments  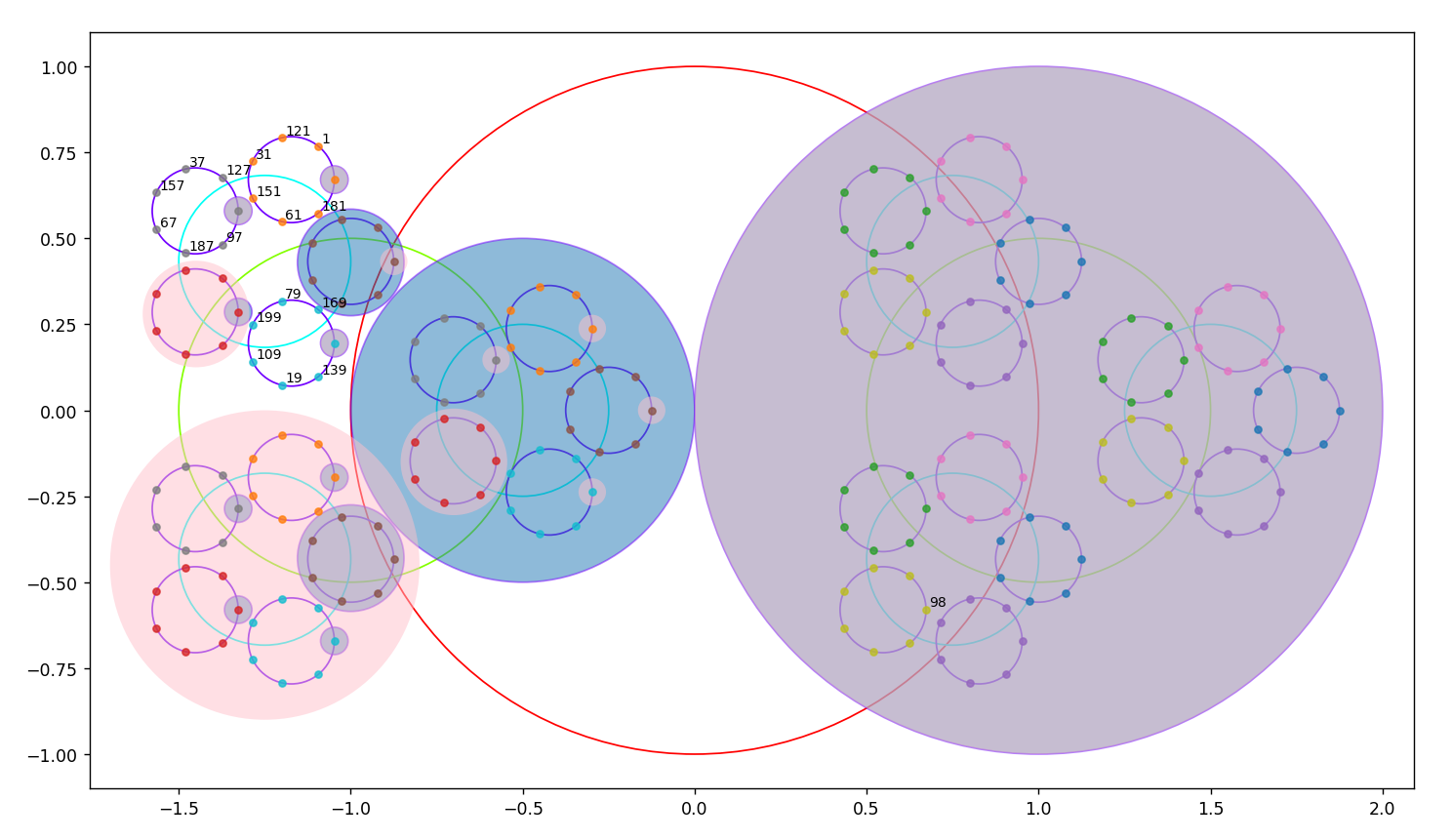  criblage par premiers décroissant jusqu’à 210 criblage par premiers décroissant jusqu’à 210 
2023 : ils semblent bien maximiser une distance... 
-
2023 : matrices de projections

-
2023 : Nombres premiers et valeurs propres

2023 : Comment une valeur propre de matrice peut-elle permettre de distinguer les nombres premiers
des nombres composés ? 
2019 : un ensemble, une transformation, des traces de premiers   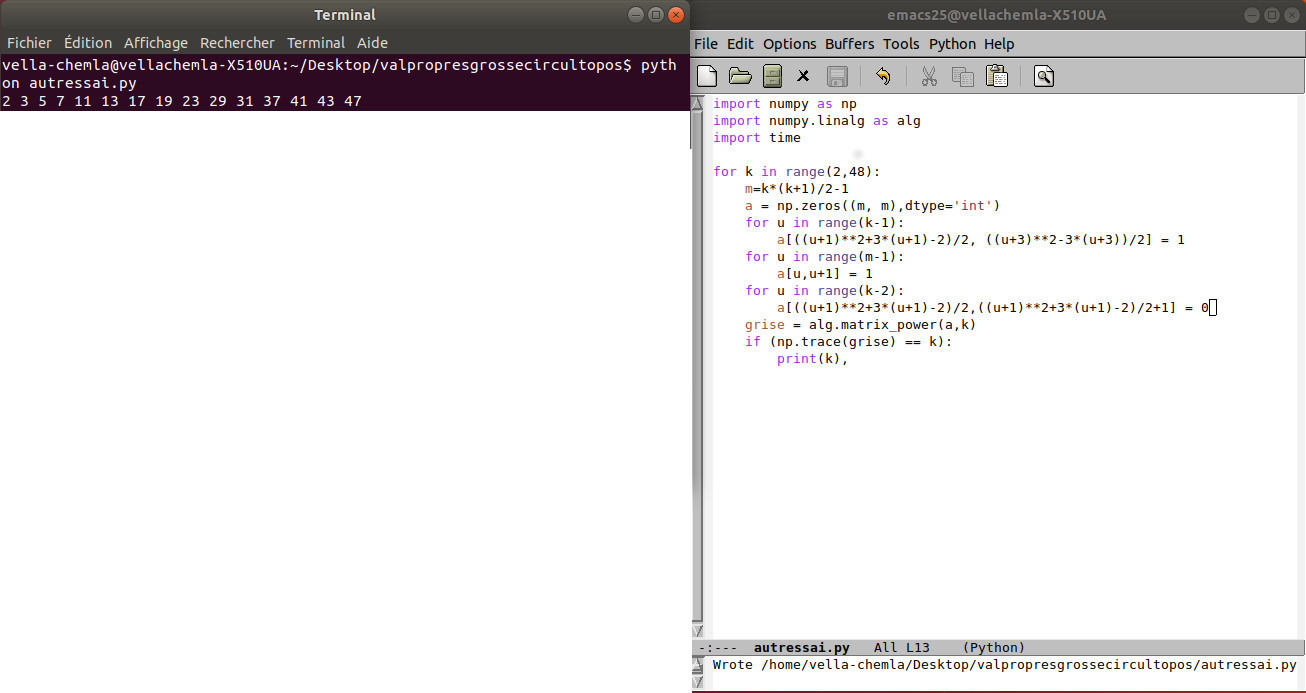
-
2023 : polytope pour décomposants de Goldbach

-
2023 : Conjecture de Goldbach et logique propositionnelle (propositions à une variable)

-
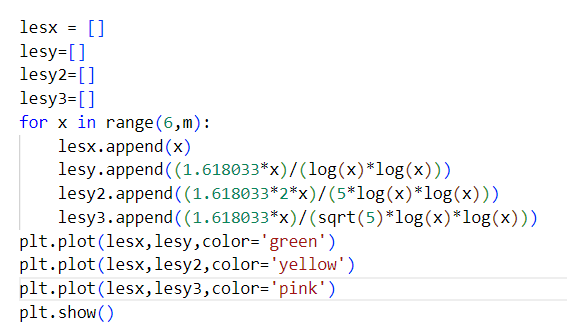
2022 : que le nombre d’or φ soit caché dans la comète des nombres de décompositions de Goldbach, ça devrait couler sous le sens ! (Les programmes sont la légende des courbes : la rouge (Prod(1-2/p).x/6, avec p premier < √x), la jaune (2φ.x/(5.log(x).log(x))) et la rose (φx/(√5.log(x).log(x))) semblent minorer la comète, la bleue semble la majorer (Prod(1-2/p).x, p premier < √x), et la verte φ.x/(log(x).log(x)) semble tomber pile au milieu des nombres de décompositions des pairs de la forme 6p, avec p premier).

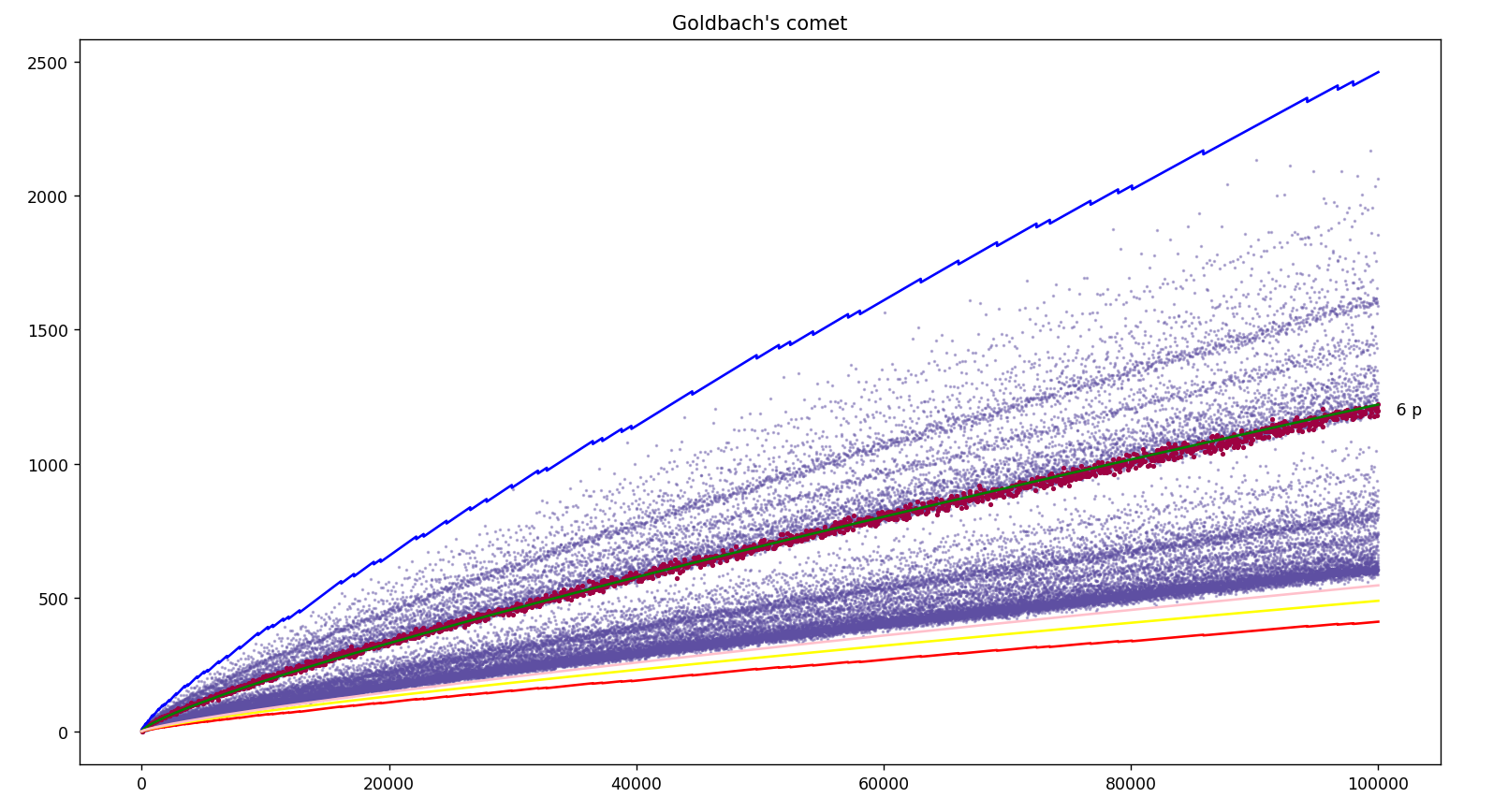  
-
2022 : Jacques Chemla démontre le lien entre formule de Chazy et formule pour la somme des diviseurs (indiqué par Dominique Giard)

-
2020 : Reprise valuations p-adiques

-
2019 : Leila m’aide

-
2019 : transformée de Fourier de la fonction qui envoie les premiers sur eux-mêmes (la somme de somme de cosinus qui me plaît tant)

-
2019 : comment perçoit-on ? (titre : Spectre lumineux) où apparaît mystérieusement une fonction triangulaire

-
2019 : Plaid écossais tropical

-
2018 : ensemble de Cantor pour les nombres premiers (un nombre premier p n’est congru à 0 que modulo lui-même, il est congru à autre chose que 0 modulo tous les autres nombres premiers q (autres que lui, i.e. q ≠ p, c’est ce dont on essaie de rendre compte en enlevant 1 classe et en gardant p-1 classes selon tout premier p (tout en haut on ne garde que 1/2 (la moitié des nombres, l’autre moitié, contenant des nombres pairs, ne pouvant contenir aucun nombre premier, sauf 2).


On n’arrive cependant pas bien à comprendre où se situent les nombres premiers dans cet ensemble dans la mesure où ils sont dans le "trou" de leur propre ligne (ils sont congrus à 0 modulo eux-mêmes donc seraient à enlever de même que tous leurs multiples) alors qu’ils sont dans les "pleins" de tous les autres nombres premiers. De plus, un ensemble fractal habituel, par définition, est auto-similaire : il a la même structure que lui-même à tout niveau ; par exemple dans l’ensemble classique de Cantor, on coupe en trois à chaque niveau (on l’appelle l’ensemble triadique) et donc la structure est toujours préservée, alors que là, au contraire, la structure est en quelque sorte perturbée (pour ne pas dire sabordée) à chaque niveau (puisqu’on change le nombre premier qui sert au découpage).
-
2018 : Essayer de comprendre la formule de Riemann

-
2018 : On réalise par programme qu’on peut remplacer le signe de l’intégrale définissant li(x) par un signe somme.
Explication : la différence entre la somme et l’intégrale est contrôlée car la dérivée de 1/log(x), qui est -1/(xlog(x)2), est intégrable.
Il faudrait du coup réussir à comprendre pourquoi Σde y=2 à x 1/ln y permet de compter π(x) le nombre de nombres premiers inférieurs ou égaux à x.
La somme des inverses des logarithmes népériens vaut par exemple 78627 pour 106 quand π(x) vaut 78498.
Elle vaut 664918 pour 107 quand π(x) vaut 664579.
 
-
2018 : Souvenir : SNURPF, exemple

-
2017 : à chaque primorielle, le nombre de points fixes augmente d’une puissance de 2.

-
2017 : Sommes de résidus modulaires



-
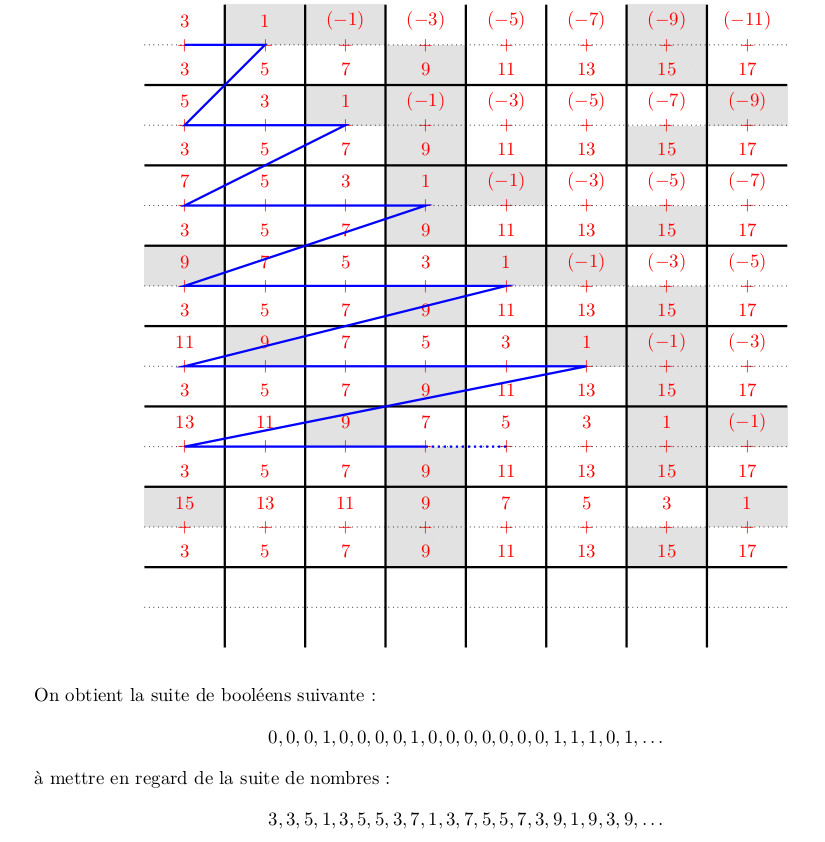
2017 : vers un pavage de Penrose

-
2017 : Un programme à mots plus courts pour connaître la primalité des entiers
 Trahtenbrot (programme python) Trahtenbrot (programme python) 
-
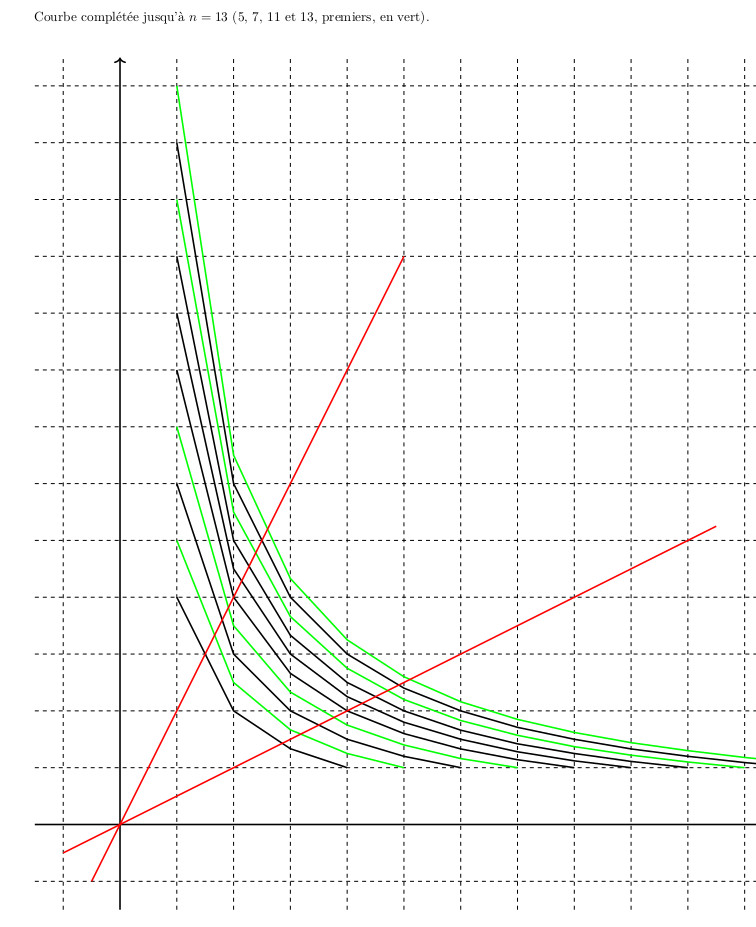
2017 : Hyperboles et mots de Christoffel

2017 : Points entiers sur hyperboles 
-
2022 : se rappeler de la note sur les mots apériodiques de 2017 (compositions des nombres "à la Knuth" et mots apériodiques pour les nombres premiers)

2019 : compositions palindromiques 
2017 : compositions puis 22N 

  
2017 : Compositions & minimiser un périmètre

-
2019 : Comme s’il en pleuvait (554)
   
-
2015 : Distance suprême

-
2015 : Spectres

-
2015 : Matrices, sommes de diviseurs, produits de restes (287)

-
2015 : Calculer l’indicateur d’Euler des nombres par un calcul matriciel

-
2015 : Calculer les sommes de diviseurs par un calcul matriciel

-
2015 : post-it : incompris, à comprendre : 3 anciennes notes regroupées sur sommes alternées de cosinus
  
-
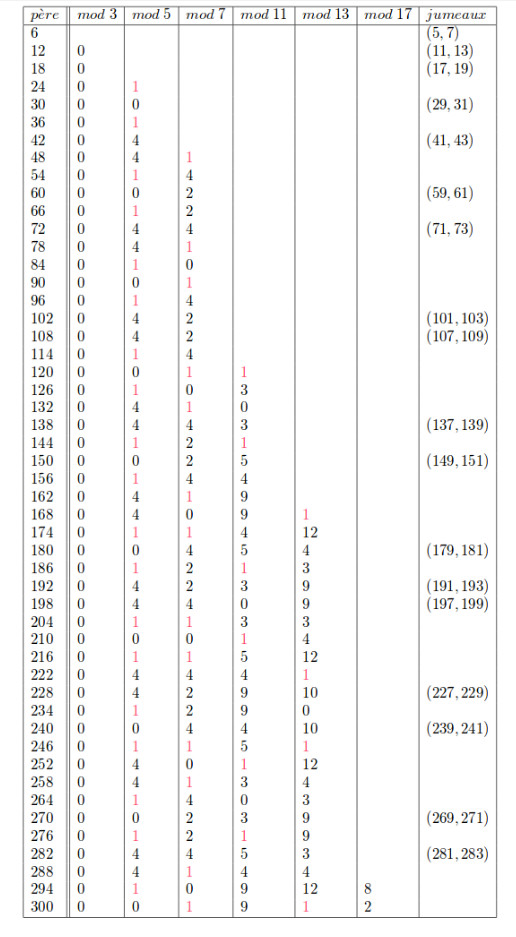
2014 : continuer de suivre Galois (ajout du problème des nombres premiers d’écart 2)


-
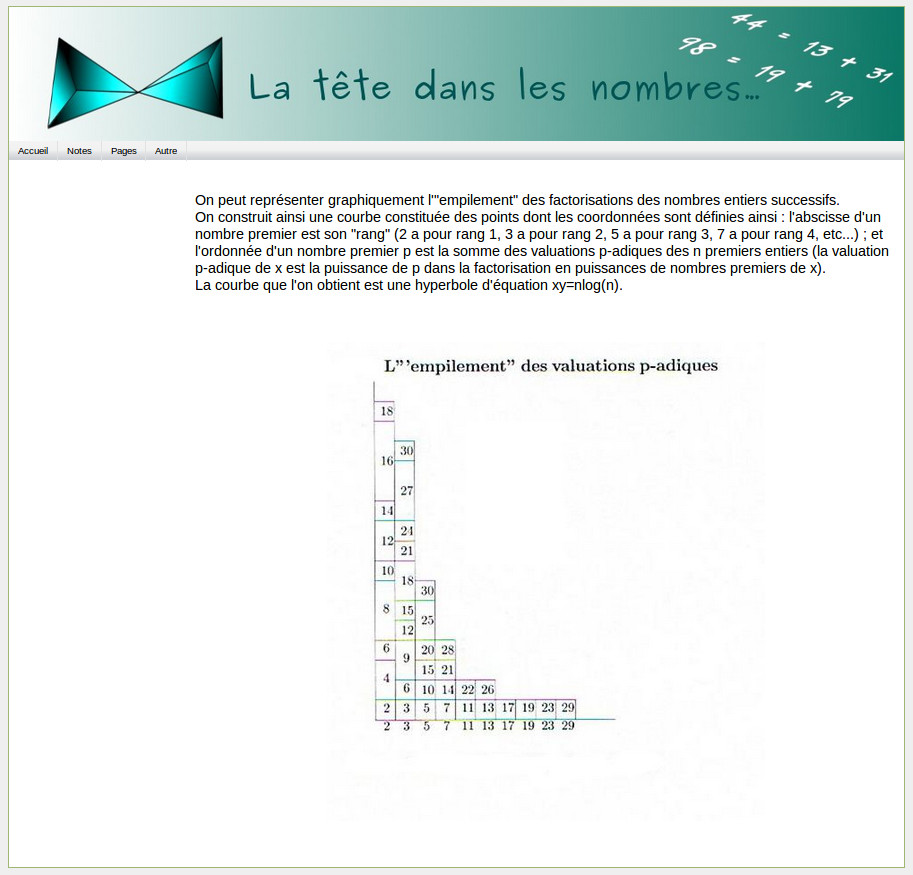
2014 : Un beau souvenir de 2005 : empilement de valuations p-adiques, en continuant de suivre Laisant
-
2012 : Conjecture des nombres premiers d’écart 2 et argument d’Euclide (note reprise) (157)

-
2011 : Une vision plus algorithmique de la conjecture de Goldbach

-
2011 : Rester éberluée face aux polynômes

-
2012 : Bonne année 2012...

2011 : Une dernière idée : utiliser la théorie de Galois pour trouver les décomposants de Goldbach... 
2011 : En attendant le 7 juin 2012 (les 270 ans de la conjecture de Goldbach), utiliser les équations algébriques pour trouver les décomposants de Goldbach... 
2011 : Une dernière idée : utiliser la théorie de Galois pour trouver les décomposants de Goldbach... 
réétudié en mai 2025 :  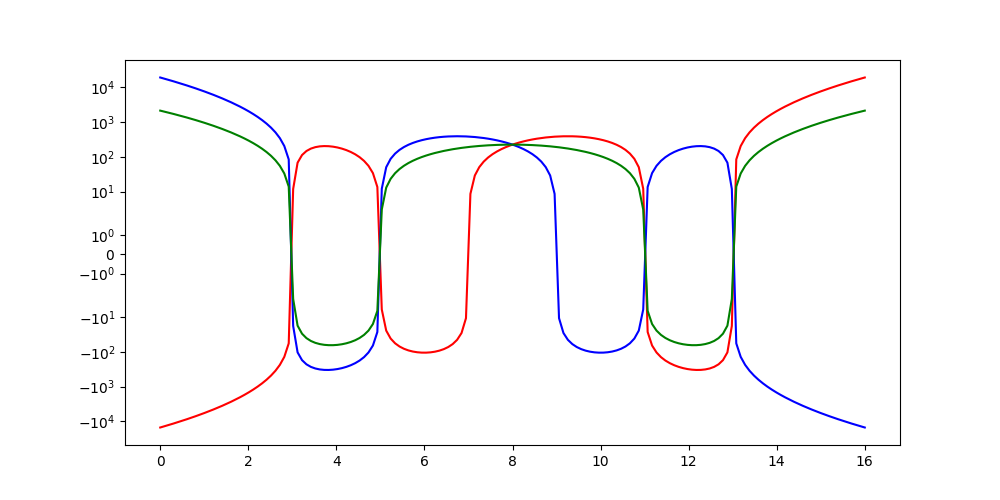 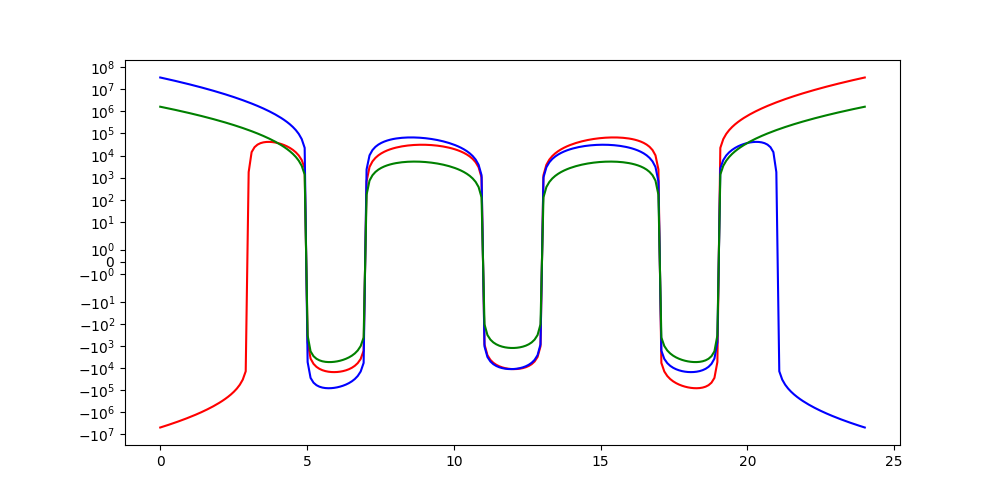
-
2009 : Reformulation de la conjecture de Goldbach dans le domaine de la combinatoire des mots

-
2006 : Fractales, symétrie et conjecture de Goldbach

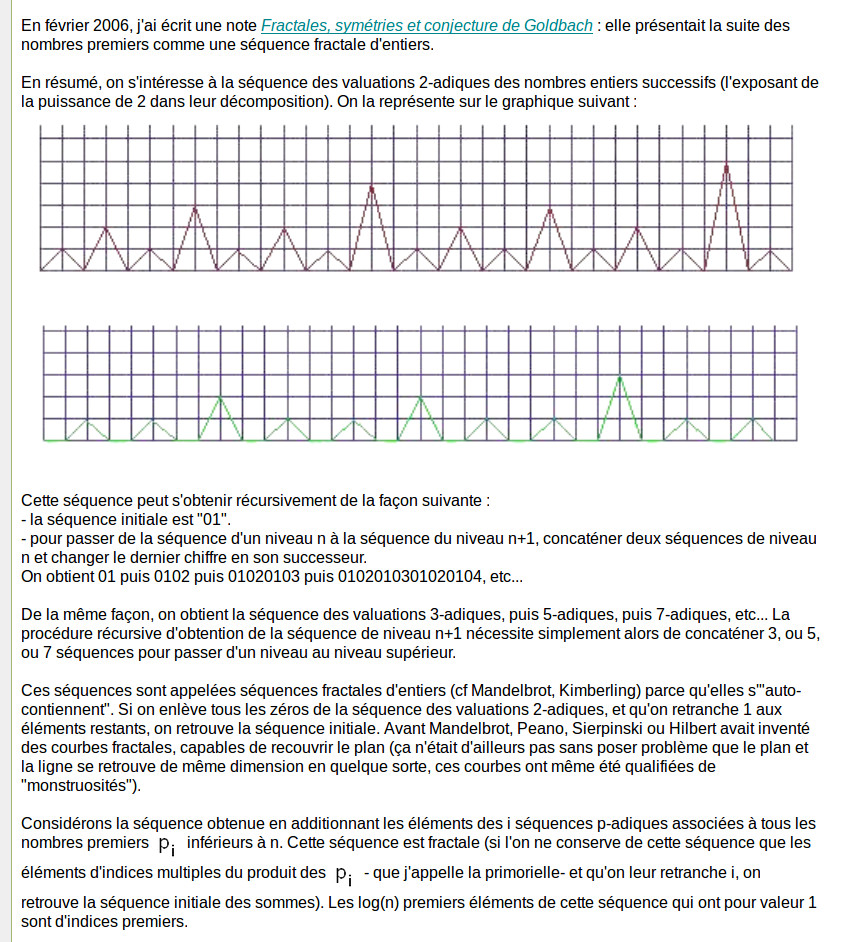  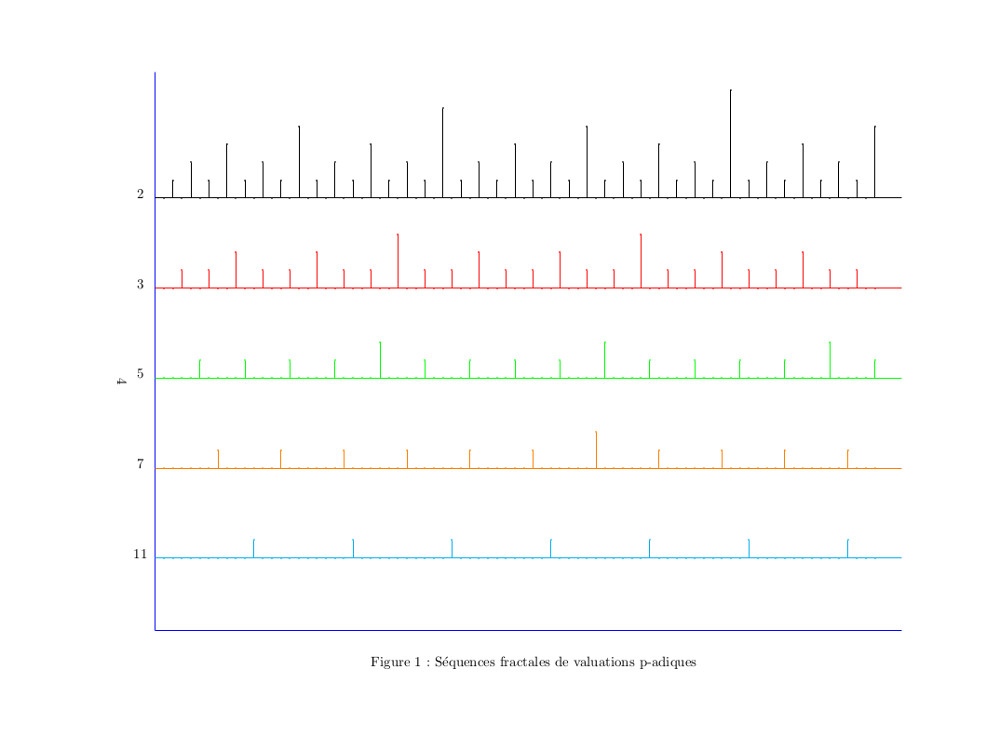 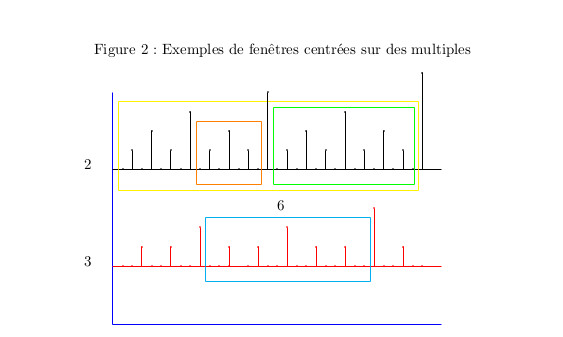 
Fractales

|