-
juillet 2025 : raccourci fatalement faux

-
16 juin 2025 : ou exclusif
 simplification : on oublie la symétrisation de la matrice, et le ou exclusif, on regarde simplement les points dont les coordonnées ne commutent pas simplification : on oublie la symétrisation de la matrice, et le ou exclusif, on regarde simplement les points dont les coordonnées ne commutent pas  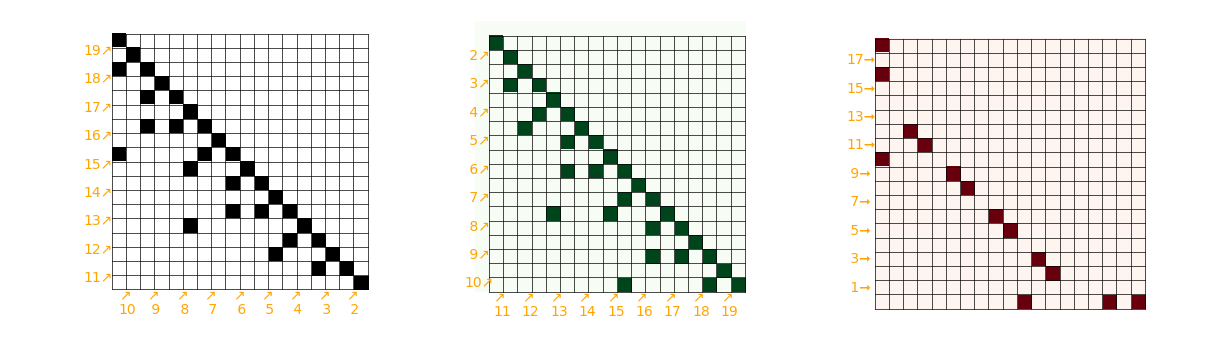 petit livret petit livret 
-
juin 2025 : décomposants de Goldbach en géométrie du plan complexe
 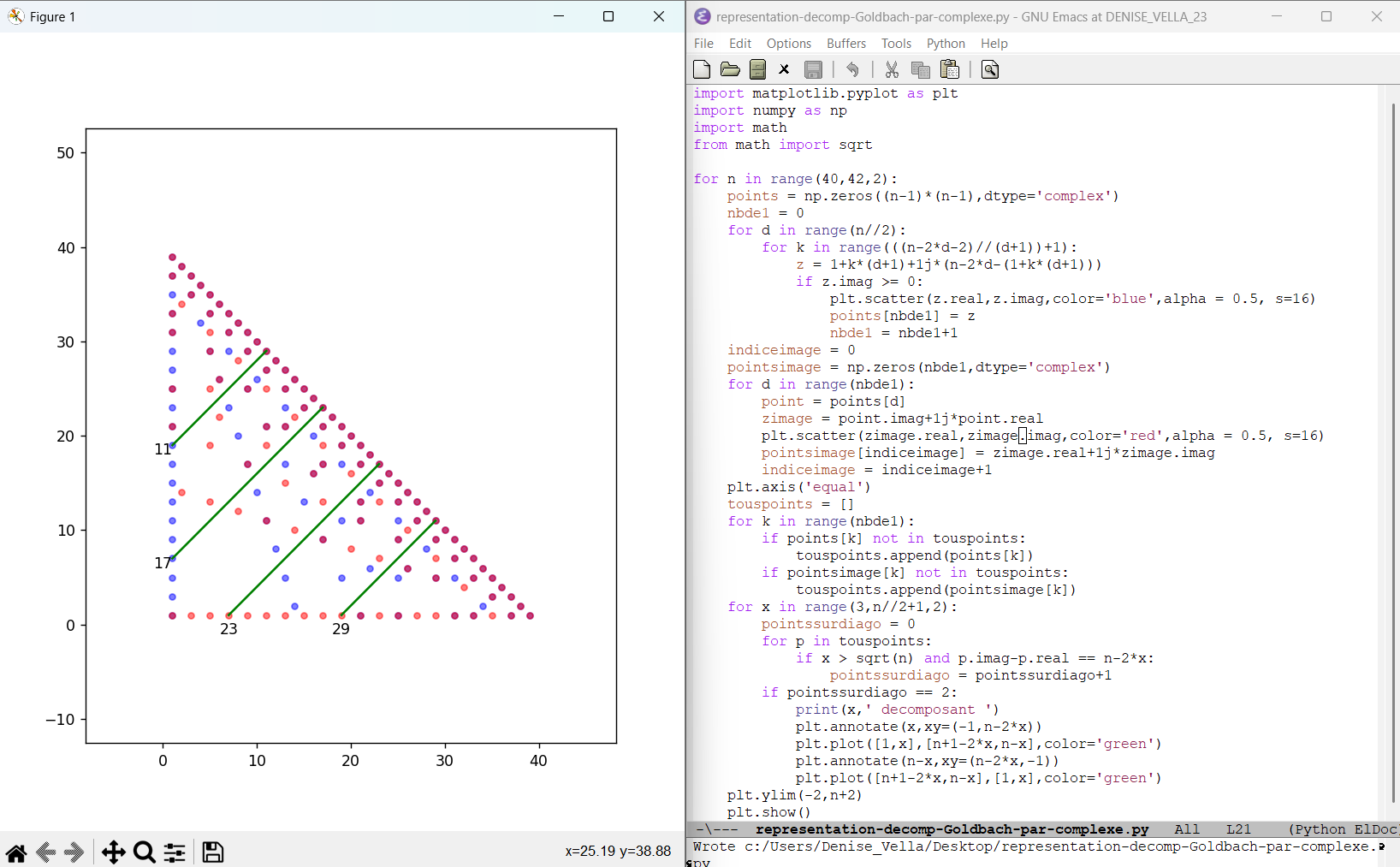
-
mai 2025 : Très constantes

-
mai 2025 : s’essayer à programmer les pavages de Penrose en python et traductions d’extraits de Noncommutative geometry à ce sujet
 
-
5.5.25 : Revenir aux équations algébriques
 programmation du test du déterminant de la matrice de Sylvester des deux polynômes à considérer pour Goldbach (et son résultat) programmation du test du déterminant de la matrice de Sylvester des deux polynômes à considérer pour Goldbach (et son résultat)    
-
mai 2025 : correspondance ouïe-vue
 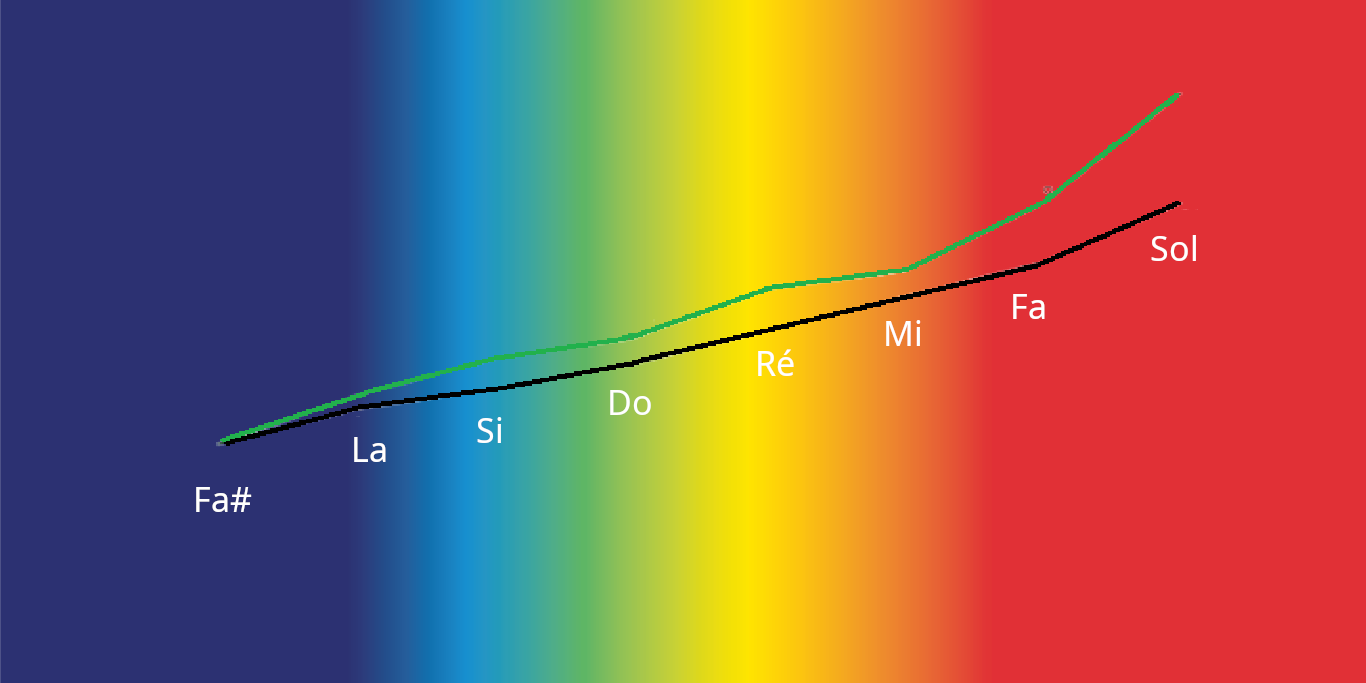
-
avril 2025 : musique : conversion fréquences des notes, nombres entiers (origine la = 440 Hertz)
  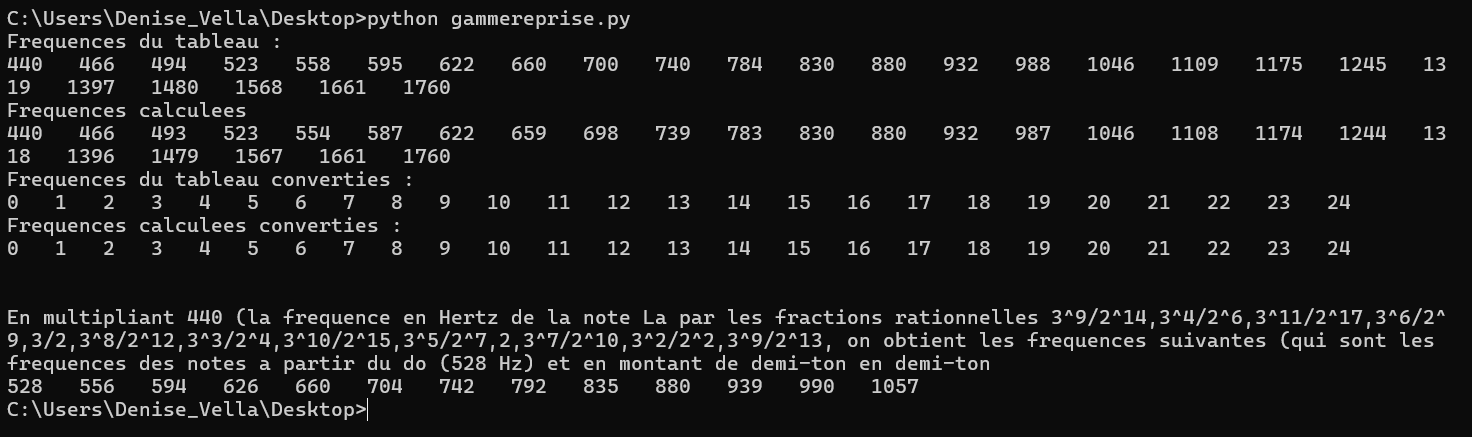
-
avril 2025 : bien comprendre la non-commutativité du langage : Transcription de Voyage autour du monde (extrait du livre Avec des nombres et des lignes d’André Sainte-Laguë)
 programmation de l’icosion et solutions programmation de l’icosion et solutions       
-
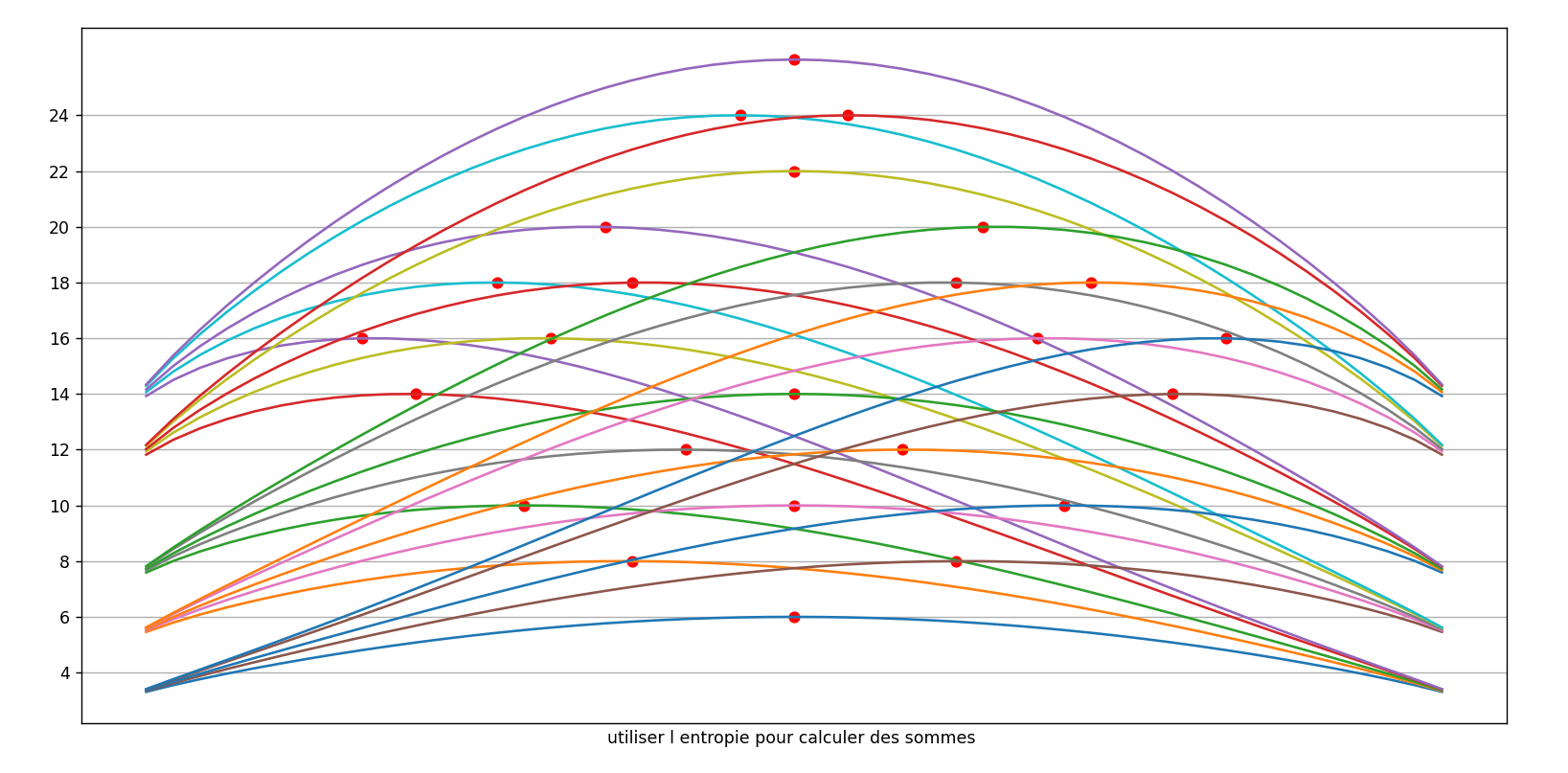
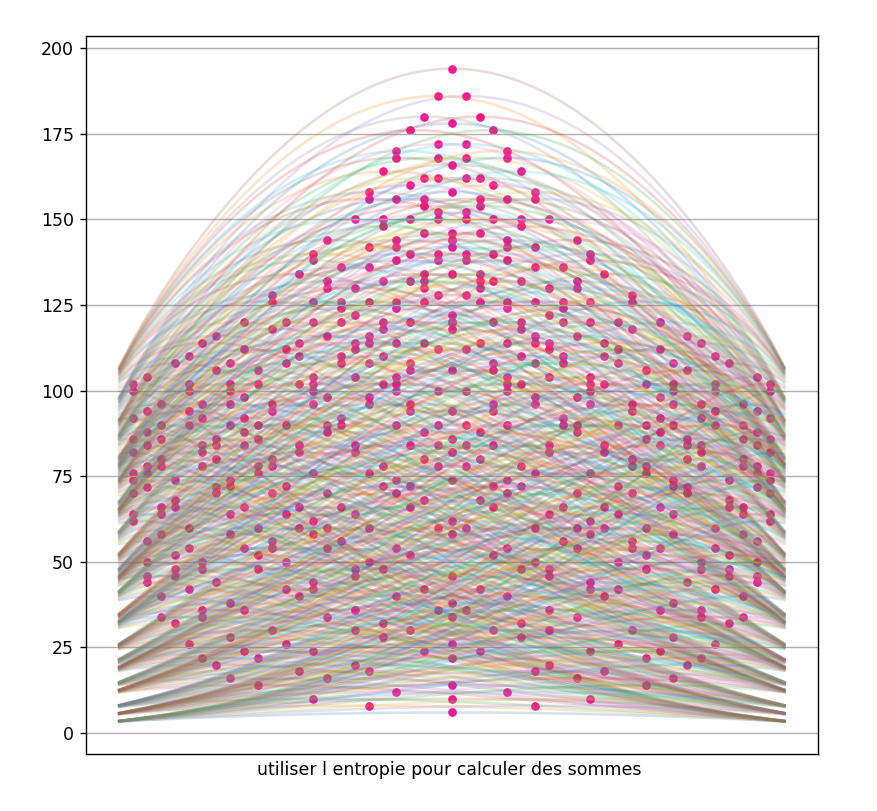
25.2.25 : L’ancien maillage que j’avais mis au jour en 2005 (voir aux pages ici et là) peut s’obtenir en calculant des sommes par utilisation de l’entropie de Shannon, entropie intervenant également en physique, ça fait plaisir ! Voici le programme utilisé pour obtenir les maximum "scatterisés" par python ci-dessous (on voit très bien 26=13+13, 24=11+13=13+11, etc.) :
 Traduction d’une référence de Maxim Kontsevich cité par Alain Connes Traduction d’une référence de Maxim Kontsevich cité par Alain Connes 
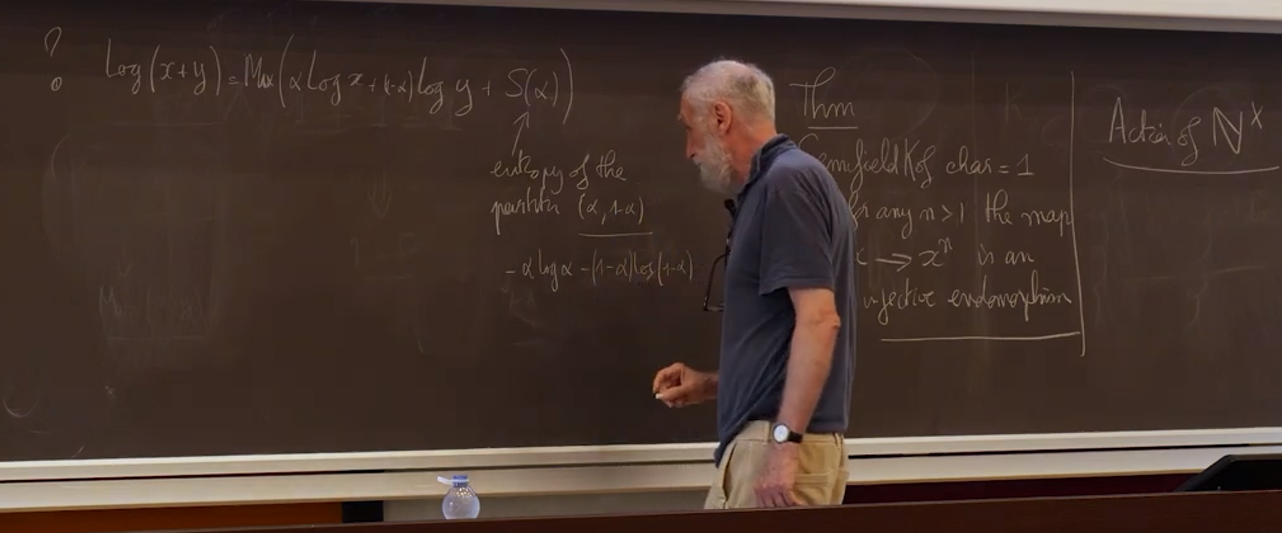  
-
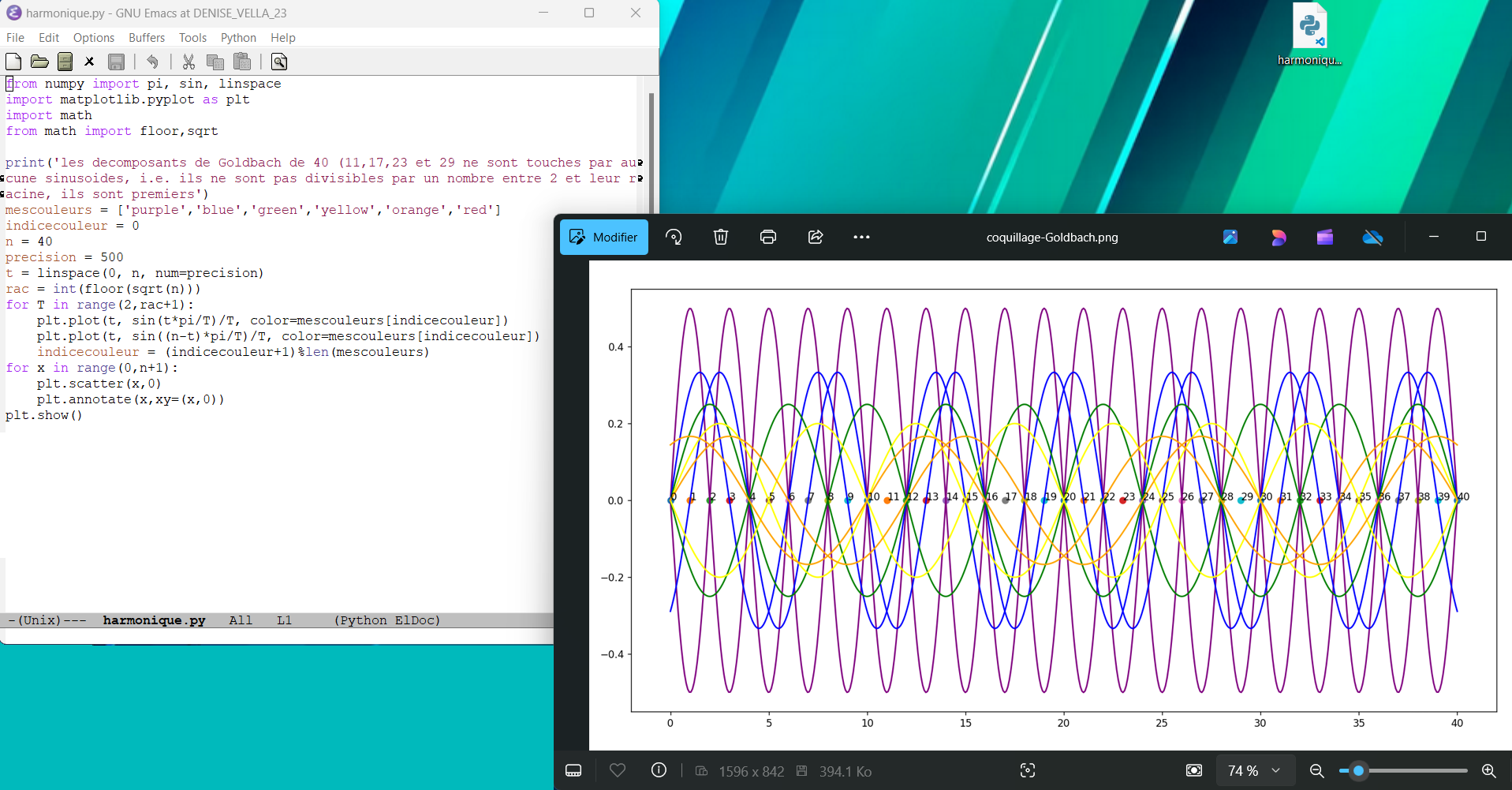
février 2025 : Harmoniques (décomposants de Goldbach de n=40)
-
2025 : certains articles fondateurs de la mécanique quantique ont 100 ans ; l’article de Paul Dirac de 1925 : Les équations fondamentales de la mécanique quantique
 l’article de Born-Jordan Sur la mécanique quantique l’article de Born-Jordan Sur la mécanique quantique  traduction du début de l’article de Born-Heisenberg-Jordan
traduction du début de l’article de Born-Heisenberg-Jordan  transcription/traduction d’un article de Delmas-Rigoutsos et d’un autre présentant opérationnellement la logique quantique transcription/traduction d’un article de Delmas-Rigoutsos et d’un autre présentant opérationnellement la logique quantique 
-
9 octobre 2024 : transcription / traduction de la thèse de Carl Friedrich Gauss
 version latine de la thèse extraite des Werke (la planche de dessins ne correspond pas à celle trouvée dans la version anglaise sur la toile) version latine de la thèse extraite des Werke (la planche de dessins ne correspond pas à celle trouvée dans la version anglaise sur la toile)  mars 2024 : Transcription en LaTeX de la Section troisième des Recherches arithmétiques de Carl Friedrich Gauss mars 2024 : Transcription en LaTeX de la Section troisième des Recherches arithmétiques de Carl Friedrich Gauss  un texte explicatif de J.-P. Friedelmeyer un texte explicatif de J.-P. Friedelmeyer  
-
22 février 2024 : exponentielle et logarithme : Des intérêts composés (petit encart devoir d’Évariste, et dédicace spéciale à grand-papa Lulu, qui m’a appris à factoriser, et le célèbre holorime aussi)
 étonnement constant étonnement constant  Compléments par Pierre de la Harpe Compléments par Pierre de la Harpe  de ce fait, image du résultat d’un programme python d’expression du log par une racine "beaucoup"-ième de ce fait, image du résultat d’un programme python d’expression du log par une racine "beaucoup"-ième   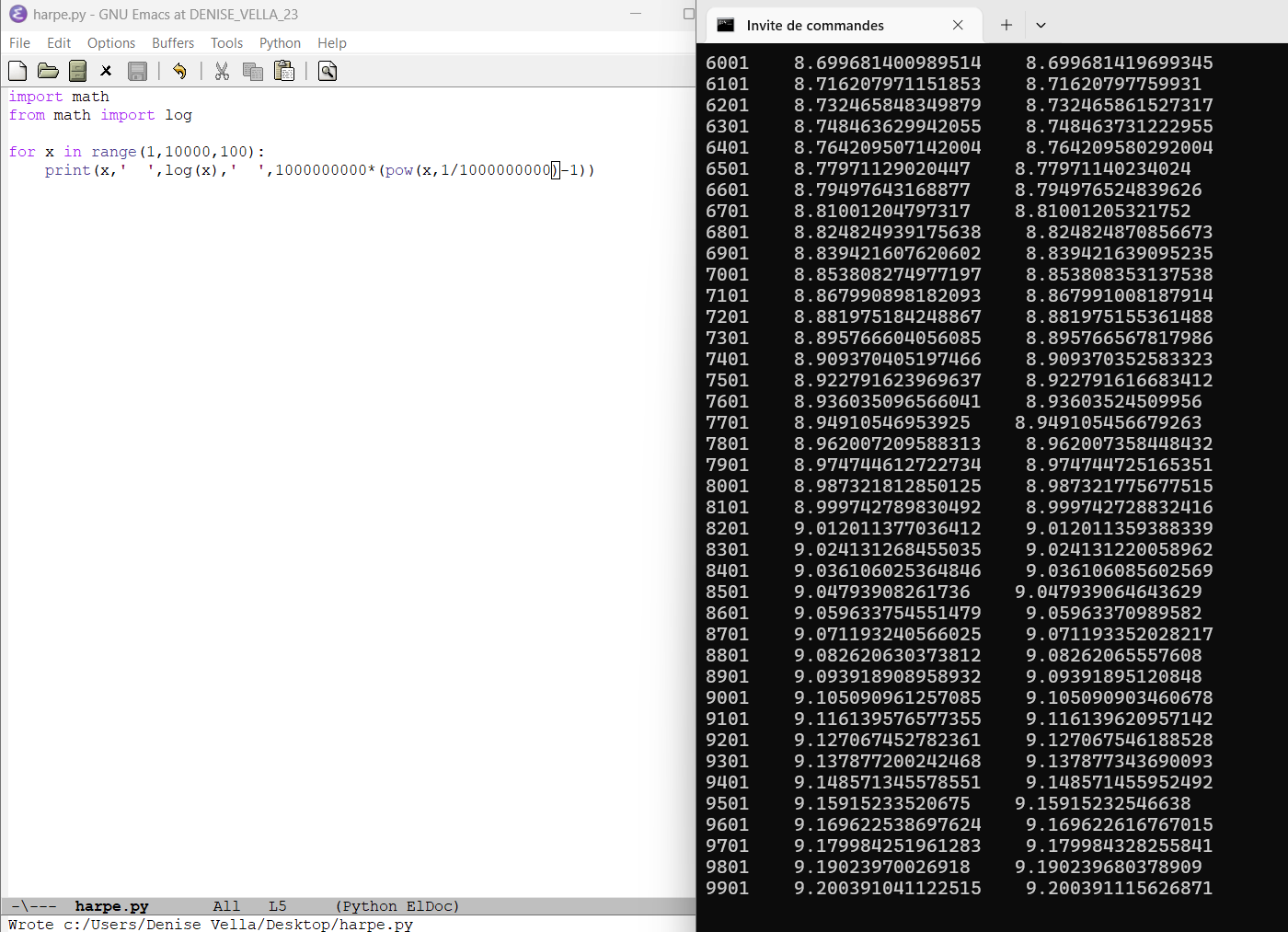
-
juillet 2023 : graphique 1 : enfin ma surface bosselée avec les décompositions de Goldbach qui ’’tombent au sol’’ (z=0) en python, graphique 2 : Plaid Goldbach vu de dessus (on distingue en foncé 3+3, 3+5, 3+7), graphique 3 : les nombres premiers de 3 à 19 vus en coupe de profil de la surface bosselée, et enfin, plaid 500 en python
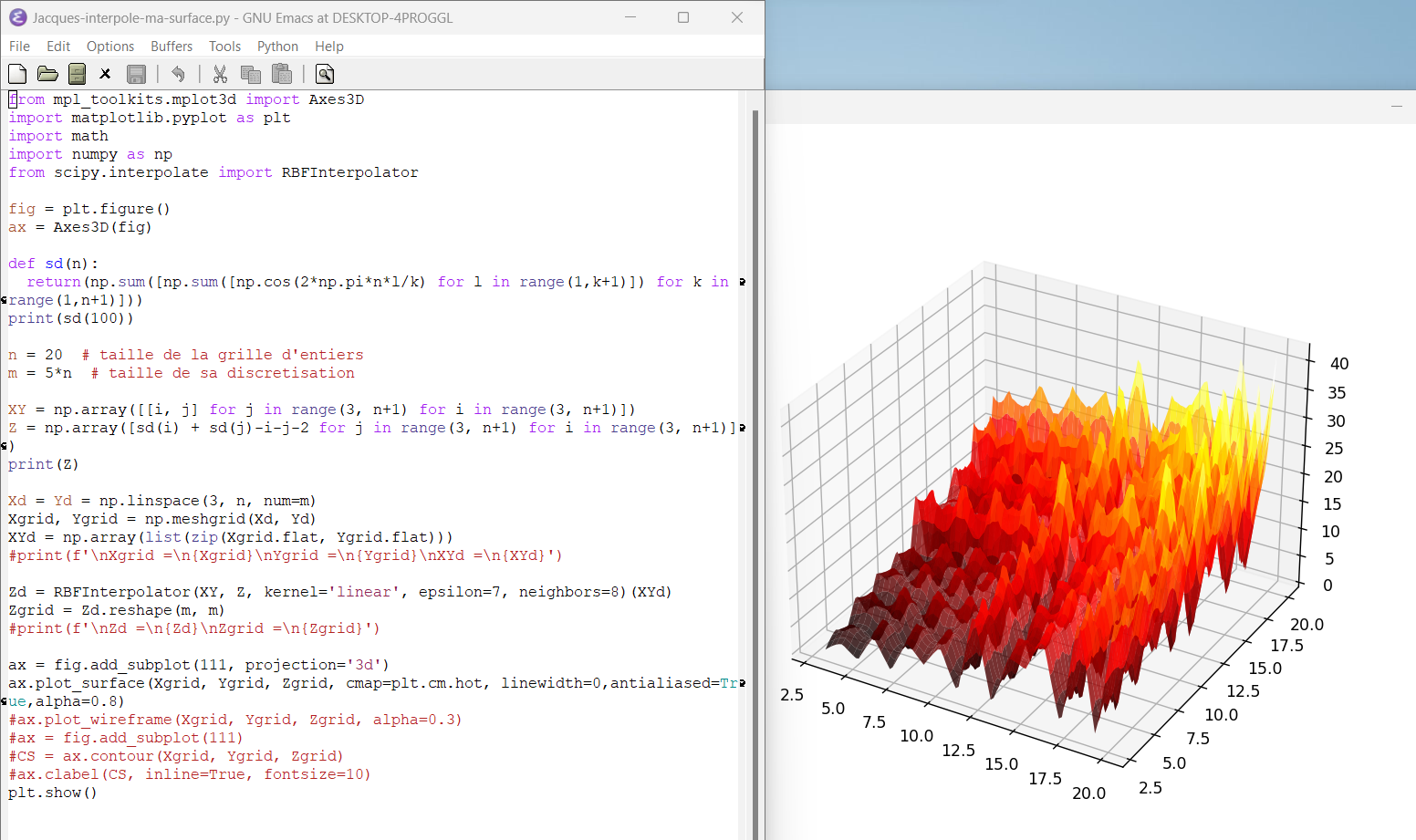 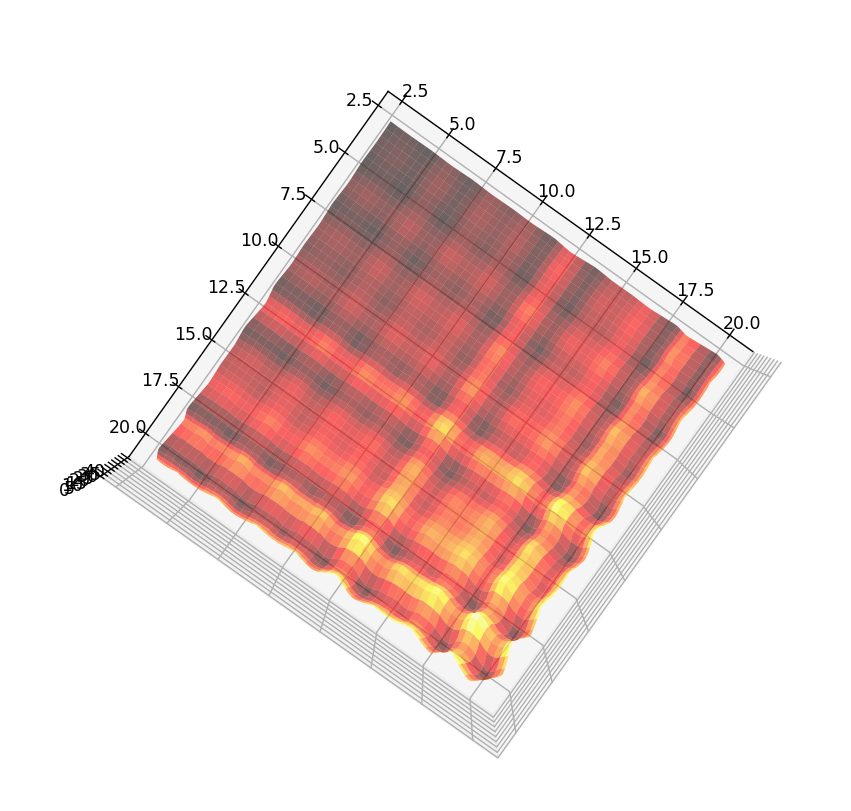 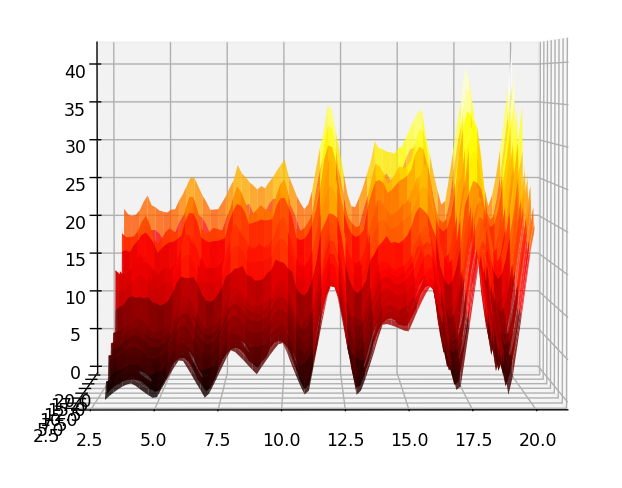 
-
31.12.2018 : Dancing Links pour Conjecture de Goldbach, selon le Christmas tree de Donald Knuth
 Christmas Trees Christmas Trees 
 
-
janvier 2023 : Conjecture de Goldbach et logique propositionnelle (propositions à une variable)
 (en) (en) 
-
25 décembre 2022 : Comète de Goldbach et Golden ratio (nombre d’or)

-
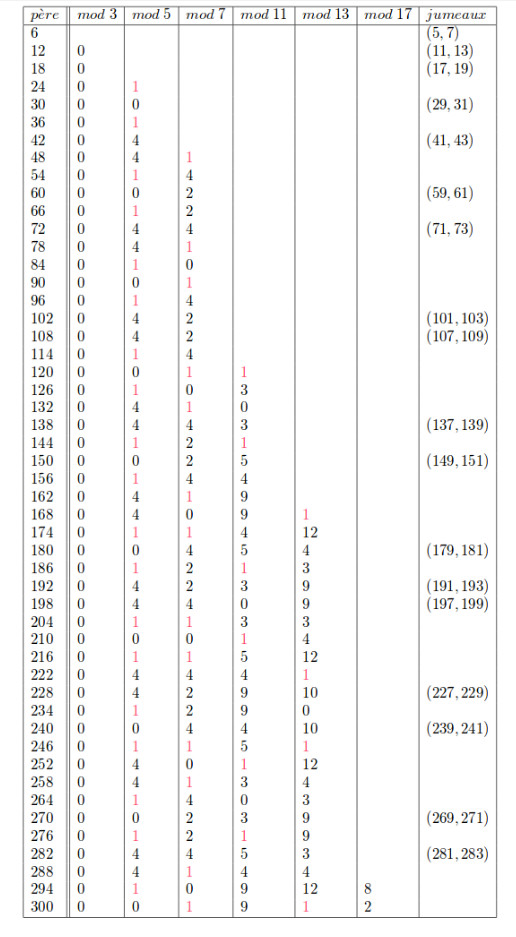
17.5.2014 : continuer de suivre Galois (ajout du problème des nombres premiers d’écart 2)


-
Juillet 2022 : moins deux (690)
 article de Rosser et Schoenfeld en référence article de Rosser et Schoenfeld en référence 
-
26.1.2019 : où l’on retrouve ζ autrement
 31.5.2019 : 31.5.2019 :  (en) (en)  23.7.2019 : annexe 23.7.2019 : annexe 
|
Christian Goldbach (18.3.1690, Königsberg (maintenant Kaliningrad), 20.11.1764, Moscou).
Léonard Euler (15.4.1707, Bâle, 18.9.1783, Saint-Pétersbourg).
Carl Frédéric Gauss (30.4.1777, Brunswick, 23.2.1855, Göttingen).
Georg Cantor (3.3.1845, Saint-Pétersbourg, 6.1.1918, Hall).
George Boole (2.11.1815, Lincoln, 8.12.1864, Ballintemple).
Alan Turing (23.6.1912, Londres, 7.6.1954, Cheshire).
En 1742, date de la conjecture, Goldbach a 52 ans, Euler en a 35, Gauss -35, et moi -222.
|
|