Dans cette page, on recherche les nombres premiers permettant d'obtenir une décomposition de 2x = 98.
Il y en a 3 : 19, 31 et 37.
On renseigne la table ci-dessous, qui a comme en-tête des lignes et des colonnes les nombres premiers inférieurs à x=49 (la moitié de 98).
La case (p1,p2) contient le reste de p1 modulo p2.
On colorie ensuite dans cette table les restes de 98 modulo chacun des nombres premiers.

Ces restes sont :
98 2 (mod 3)
98 3 (mod 5)
98 0 (mod 7)
98 10 (mod 11)
98 7 (mod 13)
98 13 (mod 17)
98 3 (mod 19)
98 6 (mod 23)
98 11 (mod 29)
98 5 (mod 31)
98 24 (mod 37)
98 16 (mod 41)
98 12 (mod 43)
98 4 (mod 47)

3 5 7 11 13 17 19 23 29 31 37 41 43 47
3 0 3 3 3 3 3 3 3 3 3 3 3 3 3
5 2 0 5 5 5 5 5 5 5 5 5 5 5 5
7 1 2 0 7 7 7 7 7 7 7 7 7 7 7
11 2 1 4 0 11 11 11 11 11 11 11 11 11 11
13 1 3 6 2 0 13 13 13 13 13 13 13 13 13
17 2 2 3 6 4 0 17 17 17 17 17 17 17 17
19 1 4 5 8 6 2 0 19 19 19 19 19 19 19
23 2 3 2 1 10 6 4 0 23 23 23 23 23 23
29 2 4 1 7 3 12 10 6 0 29 29 29 29 29
31 1 1 3 9 5 14 12 8 2 0 31 31 31 31
37 1 2 2 4 11 3 18 14 8 6 0 37 37 37
41 2 1 6 8 2 7 3 18 12 10 4 0 41 41
43 1 3 1 10 4 9 5 20 14 12 6 2 0 43
47 2 2 5 3 8 13 9 1 18 16 10 6 4 0

On voit que les nombres premiers permettant d'obtenir une décomposition Goldbach de 98 sont incongrus à 98 quelque soit le nombre premier inférieur à 49 considéré (du coup, leur complémentaire est premier).

Démontrer la conjecture revient donc à démontrer qu'il ne peut jamais y avoir au moins une case coloriée dans chaque ligne.
(remarque : les colonnes des nombres premiers supérieurs à 2x/3 ne peuvent pas contenir de cases coloriées.) Autre façon de voir les choses : prenons l'exemple du nombre pair 40.
Ci-dessous sont dessinés les résidus possibles selon chaque nombre premier inférieur à 20 (3 classes de congruence modulo 3, 5 classes de congruence modulo 5, etc).
Par convention, on dessine la classe 0 à l'extrême-gauche du dessin.
Les points bleus représentent l'appartenance de 40. 3 permet de trouver une décomposition Goldbach de 40 car 3 n'est jamais dans le même ensemble de congruence que 40. Démontrer la conjecture de Goldbach consiste donc à démontrer qu'il existe toujours un nombre premier qui ne partage aucune classe de congruence avec 2x.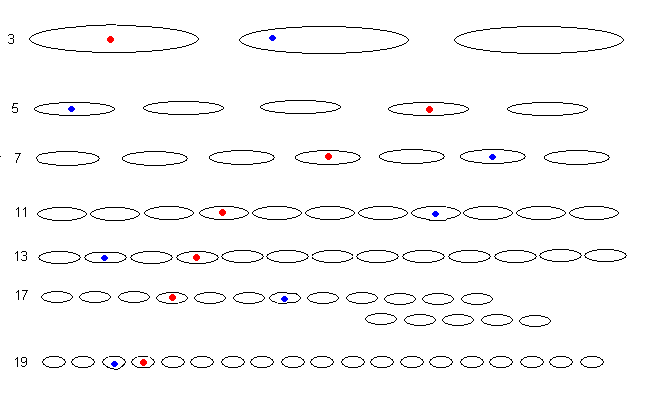


Ces découvertes fournissent-elles une preuve de la conjecture de Goldbach ?
La table fournie pour le cas 98 est en fait sous-table d'une table de congruence complète, que nous allons fournir ici pour le cas 40, de façon à conserver une certaine lisibilité.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
3 1 0 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
4 0 1 0 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
5 1 2 1 0 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
6 0 0 2 1 0 6 6 6 6 6 6 6 6 6 6 6 6 6 6
7 1 1 3 2 1 0 7 7 7 7 7 7 7 7 7 7 7 7 7
8 0 2 0 3 2 1 0 8 8 8 8 8 8 8 8 8 8 8 8
9 1 0 1 4 3 2 1 0 9 9 9 9 9 9 9 9 9 9 9
10 0 1 2 0 4 3 2 1 0 10 10 10 10 10 10 10 10 10 10
11 1 2 3 1 5 4 3 2 1 0 11 11 11 11 11 11 11 11 11
12 0 0 0 2 0 5 4 3 2 1 0 12 12 12 12 12 12 12 12
13 1 1 9 3 1 6 5 4 3 2 1 0 13 13 13 13 13 13 13
14 0 2 2 4 2 0 6 5 4 3 2 1 0 14 14 14 14 14 14
15 1 0 3 0 3 1 7 6 5 4 3 2 1 0 15 15 15 15 15
16 0 1 0 1 4 2 0 7 6 5 4 3 2 1 0 16 16 16 16
17 1 2 1 2 5 3 1 8 7 6 5 4 3 2 1 0 17 17 17
18 0 0 2 3 0 4 2 0 8 7 6 5 4 3 2 1 0 18 18
19 1 1 3 4 1 5 3 1 9 8 7 6 5 4 3 2 1 0 19
20 0 2 0 0 2 6 4 2 0 9 8 7 6 5 4 3 2 1 0

Dans la colonne de v sont colorés les nombres u congrus à 2x (ici 40) selon v.
Cela a pour conséquence que dans chaque ligne u sont colorés les nombres se trouvant dans la colonne d'un diviseur de 2x-u. Par exemple, dans la première ligne, on lit que 3 et 13 divisent 39. Dans la quatrième ligne, on lit tous les diviseurs de 36.
Lorsqu'aucune case n'est colorée dans une ligne, le nombre 2x-u est premier. Il y a forcément de telles lignes sans case colorée car si tel n'était pas le cas, cela aurait pour conséquence une contradiction avec le théorème de Tchebychev (preuve du postulat de Bertrand) qui exprime qu'il y a toujours un nombre premier entre x et 2x. Il y a donc forcément une ligne qui ne contient pas de case colorée. Reste seulement à prouver qu'une telle ligne existe pour un nombre premier.